
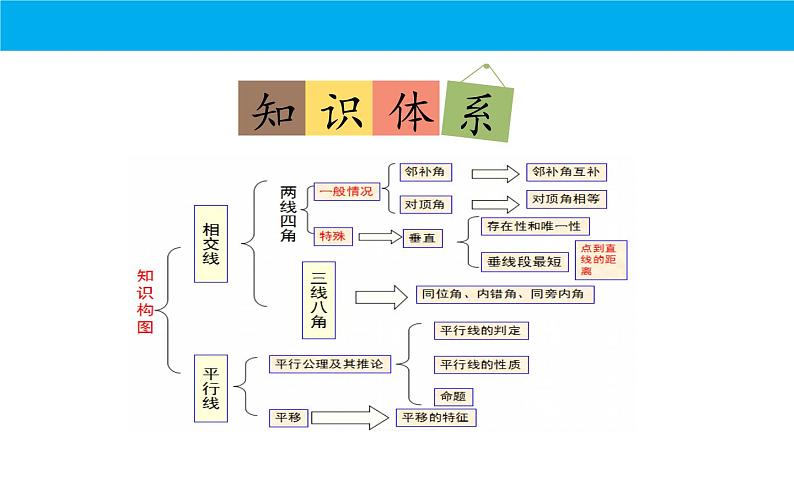




人教版七年级数学下学期期末复习课件—相交线与平行线
展开例1 如图,直线AB,CD,EF相交于点O,且AB⊥CD,∠1=25°,求∠2的度数.
∵直线AB,CD,EF相交于点O,且AB⊥CD∴∠BOC=90°,∵∠1=25°,∴∠BOE=65°,∴∠2=∠BOE=65°.
例2 已知,如图,直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE,∠COF=34°,求∠AOC和∠BOD的度数.
解:∵∠COE=90°,∠COF=34°,∴∠EOF=∠COE﹣∠COF=56°,∵OF是∠AOE的平分线,∴∠AOE=2∠EOF=112°,∴∠AOC=112°﹣90°=22°,∵∠BOD和∠AOC是对顶角,∴∠BOD=22°.
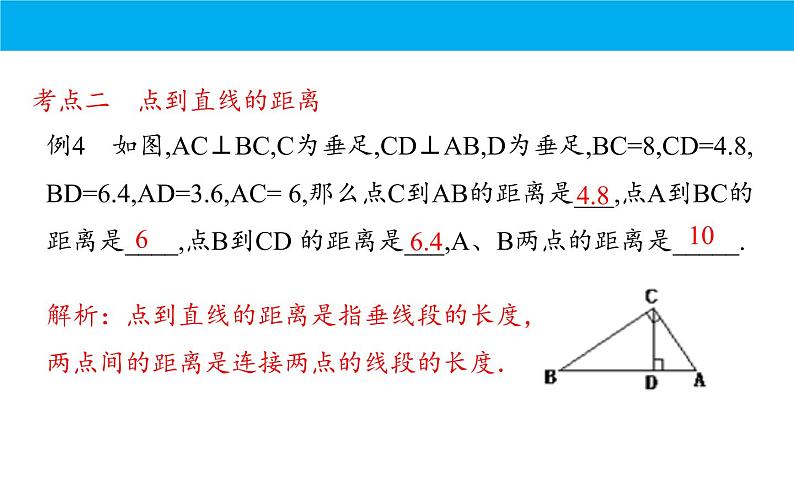
例4 如图,AC⊥BC,C为垂足,CD⊥AB,D为垂足,BC=8,CD=4.8, BD=6.4,AD=3.6,AC= 6,那么点C到AB的距离是___,点A到BC的距离是____,点B到CD 的距离是___,A、B两点的距离是_____.
解析:点到直线的距离是指垂线段的长度,两点间的距离是连接两点的线段的长度.
考点二 点到直线的距离
解 :∵OP⊥EF,∴∠EOP=90°.又∵∠EOB+∠POE+∠AOP=180°,∴∠EOB=180°-∠AOP-∠POE.∵∠AOP=30°,∴∠EOB=180°-30°-90°=60°.∵AB∥CD,∴∠EMD=∠EOB=60°.
例5 如图,已知直线AB∥CD,直线EF分别与AB,CD相交于点O,M,射线OP在∠AOE的内部,且OP⊥EF,垂足为点O.若∠AOP=30°,求∠EMD的度数.
考点三 平行线的性质与判定
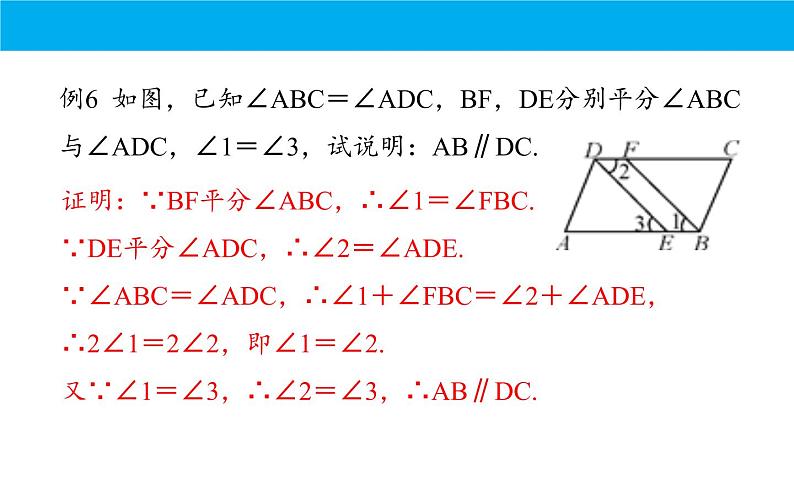
例6 如图,已知∠ABC=∠ADC,BF,DE分别平分∠ABC与∠ADC,∠1=∠3,试说明:AB∥DC.
证明:∵BF平分∠ABC,∴∠1=∠FBC.∵DE平分∠ADC,∴∠2=∠ADE.∵∠ABC=∠ADC,∴∠1+∠FBC=∠2+∠ADE,∴2∠1=2∠2,即∠1=∠2.又∵∠1=∠3,∴∠2=∠3,∴AB∥DC.
解:(1)∵AC∥DE,∴∠1=∠C,∵∠AFD=∠1,∴∠AFD=∠C,∴DF∥BC;
例7 如图,∠AFD=∠1,AC∥DE.(1)试说明:DF∥BC;(2)若∠1=68°,DF平分∠ADE,求∠B的度数.
解:(2)∵DF∥BC,∴∠EDF=∠1=68°,∵DF平分∠ADE,∴∠EDA=∠EDF=68°,∵∠ADE=∠1+∠B∴∠B=∠ADE-∠1=68°+68°-68°=68°.
例8 如图,将边长为4个单位的等边△ABC沿边BC向右平移2个单位得到△DEF,则四边形ABFD的周长?
解:∵将边长为4个单位的等边△ABC沿边BC向右平移2个单位得到△DEF,∴AD=BE=2,各等边三角形的边长均为4.∴四边形ABFD的周长=AD+AB+BE+FE+DF=16.
例9 如图,直线AB、CD、EF相交于一点O,∠AOD=3∠AOF,∠AOC=120°,求∠BOE的度数.
解:设∠AOF=x,则∠AOD=3x,根据题意得:3x+120°=180°,解得x=20°.∴∠AOF=20°,∵∠BOE=∠AOF,∴∠BOE=20°.∴∠BOE=20°.
考点四 相交线中的思想方法(方程思想、转化思想)
例10 如图,凯瑞酒店准备进行装修,把楼梯铺上地毯,已知楼梯的宽度是2米,楼梯的总长度为8米,总高度为6米,已知这种地毯每平方米的售价是60元.请你帮助酒店老板算下,购买地毯至少需要多少元?
解:利用平移线段,构成一个矩形,即可得地毯的长度为6+8=14(米),地毯的面积为14×2=28(m2),故买地毯至少需要28×60=1680(元).
1.如图,AD为△ABC的高,能表示点到直线(线段)的距离的线段有( )A.2条 B.3条 C.4条 D.5条
2.下列说法中不正确的是( )①过两点有且只有一条直线②连接两点的线段叫两点的距离③两点之间线段最短④点B在线段AC上,如果AB=BC,则点B是线段AC的中点A. ① B. ② C. ③ D. ④
3.如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则∠2等于( ).A. 30° B. 40° C. 50° D. 60°4.如图,AB∥CD,EF⊥AB于E,若∠1=60°,则∠2的度数是( ).A. 35° B. 30° C. 25° D. 20°
5.如图,在一块长为12m,宽为6m的长方形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是2m),则空白部分表示的草地面积是 ( ).A. 70m2 B. 60m2 C. 48m2 D. 18m2
1.如图1,△ABC沿射线AC方向平移2cm得到△A′B′C′,若AC=3cm,则A′C=_________cm.2.如图2,∠1=∠2,∠A=75°,则∠ADC=__________.3.如图3,若AB⊥BC,BC⊥CD,则直线AB与CD的位置关系是 .
4.如图4,a∥b,M,N分别在a,b上,P为两平行线间一点,那么∠1+∠2+∠3=_____°.5.如图5所示,OP∥QR∥ST,若∠2=120°,∠3=130°,则∠1=________度.
1.如图,已知∠1=∠2,∠C=∠F.请求出∠A与∠D的数量关系,并说明理由.
解:∠A=∠D.理由如下:设∠1的对顶角为∠3,∴∠1=∠3.∵∠1=∠2,∴∠2=∠3. ∴BF∥CE.∴∠F=∠DEC.∵∠F=∠C,∴∠DEC=∠C.∴FD∥AC. ∴∠A=∠D.
2.如图,直线AB与CD相交于点O,OE⊥AB,∠EOD=2∠AOC ,求∠AOD的度数.
解:设∠AOC=x,则∠EOD=2x,∴∠BOD=∠AOC=x,∵OE⊥AB,∴∠EOB=90°,∴x+2x=90,解得x=30,∴∠BOD=30°,∴∠AOD=150°.
初中数学人教版七年级下册第五章 相交线与平行线5.1 相交线5.1.2 垂线精品复习课件ppt: 这是一份初中数学人教版七年级下册<a href="/sx/tb_c88515_t3/?tag_id=26" target="_blank">第五章 相交线与平行线5.1 相交线5.1.2 垂线精品复习课件ppt</a>,共21页。PPT课件主要包含了复习目标,相交线,两条直线相交,两条直线被第三条所截,一般情况,邻补角,对顶角,邻补角互补,对顶角相等,平行线等内容,欢迎下载使用。
北师大版七年级数学下期末复习(相交线与平行线)习题课件: 这是一份北师大版七年级数学下期末复习(相交线与平行线)习题课件,共27页。
初中数学人教版七年级下册第五章 相交线与平行线综合与测试评优课复习课件ppt: 这是一份初中数学人教版七年级下册第五章 相交线与平行线综合与测试评优课复习课件ppt,文件包含精品原创人教版数学七年级下册5《相交线与平行线章末复习》课件pptx、精品原创人教版数学七年级下册5《相交线与平行线章末复习》教案docx、精品原创人教版数学七年级下册5《相交线与平行线章末复习》检测1docx、精品原创人教版数学七年级下册5《相交线与平行线章末复习》检测2docx等4份课件配套教学资源,其中PPT共24页, 欢迎下载使用。













