





高中人教版新课标A2.2直接证明与间接证明教课课件ppt
展开【自主预习】分析法(1)概念:从_____________出发,逐步寻求使结论成立的_________,直至最后,把要证明的结论归结为判定一个明显成立的条件.
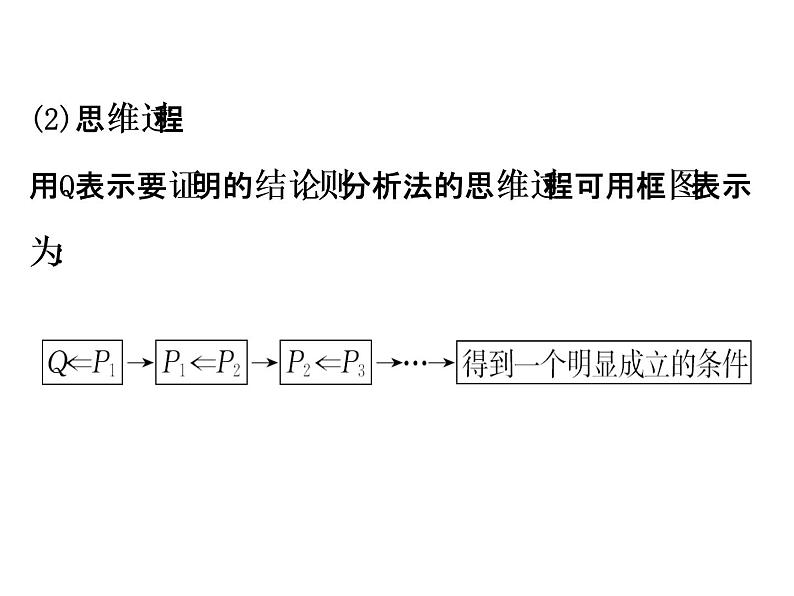
(2)思维过程用Q表示要证明的结论,则分析法的思维过程可用框图表示为:
【即时小测】1.要证 成立只需证 ( )
【解析】选C.要证 成立,即证 成立,因两数均为正数,故只需证 成立.
2.用分析法证明:欲使①A>B,只需②C
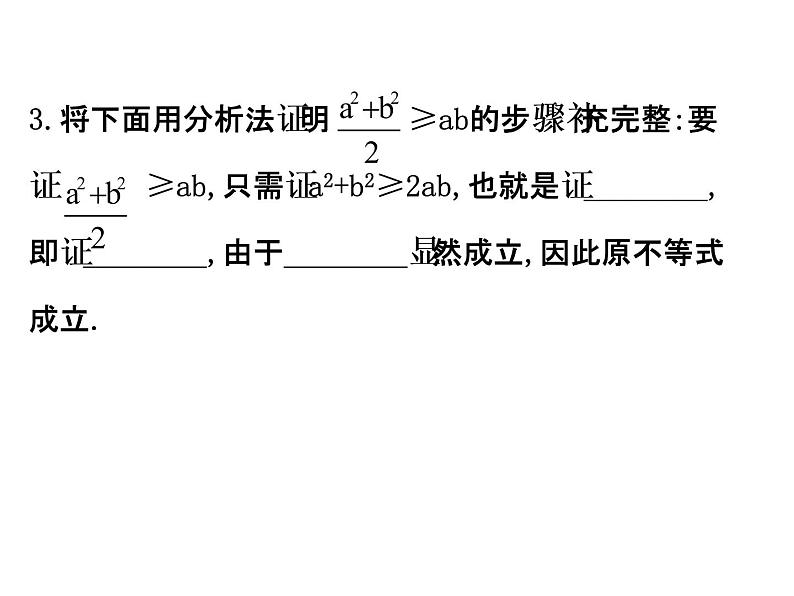
3.将下面用分析法证明 ≥ab的步骤补充完整:要证 ≥ab,只需证a2+b2≥2ab,也就是证________,即证________,由于________显然成立,因此原不等式成立.
【解析】分析法就是要证结论成立的充分条件.即应填:a2+b2-2ab≥0,(a-b)2≥0,(a-b)2≥0.答案:a2+b2-2ab≥0 (a-b)2≥0 (a-b)2≥0
【知识探究】探究点 分析法1.分析法的证明过程是“由因导果”还是执果索因?提示:分析法证明过程是执果索因,一步步寻找结论成立的充分条件.
2.分析法的优越性是什么?提示:(1)环环相扣:从结论出发,要证……,只要证……过程严密紧凑.(2)步步可逆:每一步都在寻找充分条件,因此整个过程倒过来即是综合法证明.
【归纳总结】1.分析法的特点(1)分析法的特点是从“未知”看“需知”,逐步靠拢“已知”,其逐步推理的过程,实际上是寻找使结论成立的充分条件.
(2)分析法从命题的结论入手,寻求结论成立的条件,直至归结为已知条件、定义、公理、定理等.
2.用分析法书写证明过程时的格式“要证……,只需证……,只需证……,……由于……显然成立(已知,已证…),所以原结论成立.”其中的关联词语不能省略.
3.分析法与综合法的关系(1)综合法是由因导果,步骤严谨、逐层递进、步步为营,书写表达过程条理清晰、形式简洁,宜于表达推理的思维轨迹.缺点是探路艰难、困于思考、不易达到所要证明的结论.(2)分析法是执果索因,方向明确、利于思考、思路自然,便于寻找解题思路.缺点是思路逆行、易表述出错.
易错警示:用分析法证明问题时,证明过程中“要证……;只需证……,只需证……,……,由于……显然成立,故原结论成立”的关联词不能省略,否则就不是分析法了.
类型一 分析法证明不等式【典例】1.要证:a2+b2-1-a2b2≤0,只要证明 ( )A.2ab-1-a2b2≤0B.a2+b2-1- ≤0C. -1-a2b2≤0D.(a2-1)(b2-1)≥0
2.(2016·淄博高二检测)如果 ,则实数a,b应满足的条件是________.3.(2016·郑州高二检测)已知非零向量a⊥b,求证:
【解题探究】1.典例1中的条件“a2+b2-1-a2b2如何变形?提示:因式分解.2.典例2中,如何探求a,b满足的条件?提示:采用分析法.
3.典例3中可采用什么方法来证明?提示:可采用分析法,逐步探寻不等式成立的充分条件.
【解析】1.选D.因为a2+b2-1-a2b2=(a2-a2b2)+(b2-1)=a2(1-b2)+(b2-1)=(a2-1)(1-b2)=-(a2-1)(b2-1).
故只需a≠b,且a≥0,b≥0即可.答案:a≥0,b≥0且a≠b
3.因为a⊥b,所以a·b=0要证:只需证:|a|+|b|≤ |a-b|平方得|a|2+|b|2+2|a|·|b|≤2(|a|2+|b|2)只需证:|a|2+|b|2-2|a|·|b|≥0成立.即只需证:(|a|-|b|)2≥0,它显然成立.故原不等式得证.
【方法技巧】分析法证明不等式的方法与技巧
特别提醒:逆向思考是分析法证明的立体思路,通过反推,逐步探寻使结论成立的充分条件,正确把握转化方向,使问题得以解决.切记“逆向”“反推”,否则会出现错误.
【拓展延伸】分析法证明问题的注意事项(1)对于一些含有分式、根式、对数式、指数式的不等式(等式)的命题不便于用综合法证明时,常常考虑用分析法证明.(2)分析法证明命题成立必须保证步步有理有据,转化合理,得到的结果必须是显然的,如已知条件、定理、定义、公理等.
【变式训练】已知a>5,求证:
【证明】要证 只需证 只需证 即 即只需证 只需证a2-5a
【解题探究】本例中a,b,c满足什么关系?提示:任意两边之和大于第三边.
【证明】要证明 只需证明 即可,所以 因为a>0,b>0,c>0,m>0,所以(a+m)(b+m)(c+m)>0.因为a(b+m)(c+m)+b(a+m)(c+m)-c(a+m)(b+m)
=abc+abm+acm+am2+abc+abm+bcm+bm2-abc-bcm-acm-cm2=2abm+am2+abc+bm2-cm2=2abm+abc+(a+b-c)m2.因为△ABC中任意两边之和大于第三边,所以a+b-c>0,所以(a+b-c)m2>0,
所以2abm+abc+(a+b-c)m2>0,所以
【延伸探究】1.本例增加条件“三个内角A,B,C成等差数列”求证:
【证明】要证 即证 即证 即证c(b+c)+a(a+b)=(a+b)(b+c),即证c2+a2=ac+b2.因为△ABC三个内角A,B,C成等差数列,所以B=60°.由余弦定理,有b2=c2+a2-2cacs60°,
即b2=c2+a2-ac.所以c2+a2=ac+b2成立,命题得证.
【证明】要证 只需证a+b+(a+b)c>(1+a+b)c.即证a+b>c.而a+b>c显然成立.所以
【方法技巧】1.分析法与综合法的关系分析法与综合法的关系可表示为下图:
从图中可以看出,逆向书写分析过程,同样可以完成证明,这就是综合法.由此使我们想到,用分析法探路,用综合法书写,也是一种很好的思维方式.
2.分析综合法分析法与综合法是两种思路相反的推理方法,分析法是倒溯,综合法是顺推.因此常将二者交互使用,互补优缺点,从而形成分析综合法,其证明模式可用框图表示如下:
其中P表示已知条件、定义、定理、公理等,Q表示要证明的结论.
【补偿训练】已知a,b,c是不全相等的正数,且0
【证明】要证
分析解题过程,找出错误之处,并写出正确答案.提示:错误的根本原因是解题步骤错误.把要证的结论 当成已知条件了,不符合分析法的步骤.正确解答过程如下:
【解析】因为 都是正数.所以要证 只要证明 展开得12+4 <24,即 <3,只需证5<9,因为5<9显然成立,故不等式 成立.
数学选修1-24.2结构图图片ppt课件: 这是一份数学选修1-24.2结构图图片ppt课件,共38页。PPT课件主要包含了系统结构,若干要素,从属关系,逻辑的先后关系,知识结构图,组织结构图,树形结构图,环形结构图,失误案例等内容,欢迎下载使用。
人教版新课标A选修1-24.1流程图课文配套ppt课件: 这是一份人教版新课标A选修1-24.1流程图课文配套ppt课件,共50页。PPT课件主要包含了图形符号,文字说明,一个或多个,工序流程图,工业生产,流程图如图所示,失误案例等内容,欢迎下载使用。
人教版新课标A选修1-22.2直接证明与间接证明授课课件ppt: 这是一份人教版新课标A选修1-22.2直接证明与间接证明授课课件ppt,共46页。PPT课件主要包含了充分条件,明显成立等内容,欢迎下载使用。













