









专题14 一次函数的应用-2021年中考数学二轮复习专题 学案+课件
展开2021年中考数学一轮专题复习
学案14 一次函数的应用
| 考点 | 课标要求 | 考查角度 |
1 | 待定系数法 | 会用待定系数法确定一次函数的表达式. | 多以解答题的形式考查. |
2 | 一次函数的应用问题 | 能用一次函数知识解决简单实际问题 | 多以解答题的形式考查一次函数在实际生活中的应用.也有部分地市以探究题的形式考查. |
1.确定一次函数解析式的方法:
(1)依据题意中等量关系直接列出解析式;(2)待定系数法.
2.用待定系数法求一次函数表达式的一般步骤:
确定一个正比例函数,需要确定正比例函数解析式y=kx(k≠0)中的常数k.
确定一个一次函数,需要确定一次函数解析式y=kx+b(k≠0)中的常数k和b.
解这类问题的一般方法是待定系数法.
(1)设出函数的一般形式.
(2)根据已知条件(自变量与函数的对应值)代入表达式得到关于待定系数的方程或方程组.
(3)解方程或方程组求出待定系数的值.
(4)将所求得的系数的值代入到一般形式中.
3.确定正比例函数表达式,只需一对x与y的对应值(即已知正比例函数图象上的一个点即可);确定一次函数的表达式,只需要两对x与y的对应值(即已知一次函数图象上的两个点即可).
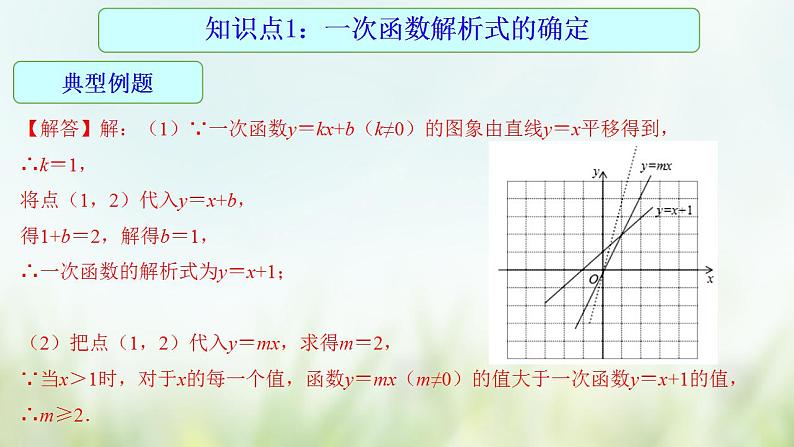
【例1】(2020•北京22/28)在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象由函数y=x的图象平移得到,且经过点(1,2).
(1)求这个一次函数的解析式;
(2)当x>1时,对于x的每一个值,函数y=mx(m≠0)的值大于一次函数y=kx+b的值,直接写出m的取值范围.
【考点】一次函数图象与系数的关系;一次函数图象与几何变换.有
【答案】见试题解答内容
【分析】(1)先根据直线平移时k的值不变得出k=1,再将点A(1,2)代入y=x+b,求出b的值,即可得到一次函数的解析式;
(2)根据点(1,2)结合图象即可求得.
【解答】解:(1)∵一次函数y=kx+b(k≠0)的图象由直线y=x平移得到,
∴k=1,
将点(1,2)代入y=x+b,
得1+b=2,解得b=1,
∴一次函数的解析式为y=x+1;
(2)把点(1,2)代入y=mx,求得m=2,
∵当x>1时,对于x的每一个值,函数y=mx(m≠0)的值大于一次函数y=x+1的值,
∴m≥2.
【点评】本题考查了一次函数图象与几何变换,一次函数与系数的关系,数形结合是解题的关键.
【例2】(2019·泸州)一次函数y=kx+b的图象经过点A(1,4),B(-4,-6),求该一次函数的解析式.
【答案】 D.
【分析】将点A(1,4),B(-4,-6)代入y=kx+b中,列出关于k和b的二元一次方程组,解方程组即可.
【解答】解:把点A(1,4),B(-4,-6)代入y=kx+b中,得:
,
解得:,
∴一次函数解析式为:y=2x+2.
【例3】(2019·柳州)己知A,B两地相距3千米,小黄从A地到B地,平均速度为4千米/小时,若用x表示行走的时间(小时),y表示余下的路程(千米),则y关于x的函数解析式是( )
A. y=4x(x≥0) B. y=4x-3(x≥)
C. y=3-4x(x≥0) D. y=3-4x(0≤x≤)
【答案】 D.
【分析】根据路程等于速度乘以时间可以算出小黄所走的路程,然后用两地的总路程减去小黄所走的路程即可得出余下的路程y与所用的时间x的函数关系式,然后根据总路程除以速度等于时间即可求出x的取值范围,从而得出答案.
【解答】解:根据题意得:
全程需要的时间为:3÷4= (小时),
∴y=3-4x(0≤x≤).
故答案为:D.
一次函数图象与坐标轴围成的三角形的面积:
直线y=kx+b与x轴的交点坐标为(,0),与y轴的交点坐标为(0,b);直线与两坐标轴围成的三角形的面积为.
【例4】(2020•陕西7/25)在平面直角坐标系中,O为坐标原点.若直线y=x+3分别与x轴、直线y=-2x交于点A、B,则△AOB的面积为( )
A.2 B.3 C.4 D.6
【考点】一次函数的性质;两条直线相交或平行问题
【分析】根据方程或方程组得到A(-3,0),B(-1,2),根据三角形的面积公式即可得到结论.
【解答】解:在y=x+3中,令y=0,得x=-3,
解得:,
∴A(-3,0),B(-1,2),
∴△AOB的面积.
故选:B.
【点评】本题考查了直线围成图形面积问题,其中涉及了一次函数的性质,三角形的面积的计算,正确的理解题意是解题的关键.
【例5】(2020•河北24/26)表格中的两组对应值满足一次函数y=kx+b,现画出了它的图象为直线l,如图.而某同学为观察k,b对图象的影响,将上面函数中的k与b交换位置后得另一个一次函数,设其图象为直线l′.
x | -1 | 0 |
y | -2 | 1 |
(1)求直线l的解析式;
(2)请在图上画出直线l′(不要求列表计算),并求直线l′被直线l和y轴所截线段的长;
(3)设直线y=a与直线l,l′及y轴有三个不同的交点,且其中两点关于第三点对称,直接写出a的值.
【考点】一次函数的性质;一次函数的图象;一次函数图象与几何变换
【分析】(1)根据待定系数法求得即可;
(2)画出直线l,求得两直线的交点,根据勾股定理即可求得直线l′被直线l和y轴所截线段的长;
(3)求得两条直线与直线y=a的交点横坐标,分三种情况讨论求得即可.
【解答】解:(1)∵直线l:y=kx+b中,当x=-1时,y=-2;当x=0时,y=1,
∴,解得,
∴直线l的解析式为y=3x+1;
(2)依题意可得直线l′的解析式为y=x+3
如图,
解得,
∴两直线的交点为A(1,4),
∵直线l′: y=x+3与y轴的交点为B(0,3),
∴直线l′被直线l和y轴所截线段的长为:;
(3)把y=a代入y=3x+1得,a=3x+1,解得;
把y=a代入y=x+3得,a =x+3,解得x = a -3;
分三种情况:①当第三点在y轴上时,,
解得;
②当第三点在直l上时,,
解得a =7;
③当第三点在直线l′上时,,
解得;
∴直线y=a与直线l,l′及y轴有三个不同的交点,且其中两点关于第三点对称,则a的值为或7或.
【点评】本题考查了一次函数图象与几何变换,两直线相交问题,待定系数法求一次函数的解析式,分类讨论是解题的关键.
【例6】(2019·沈阳)在平面直角坐标系中,直线y=kx+4(k≠0)交x轴于点A(8,0),交y轴于点B.
(1)k的值是________;
(2)点C是直线AB上的一个动点,点D和点E分别在x轴和y轴上.
①如图,点E为线段OB的中点,且四边形OCED是平行四边形时,求□OCED的周长;
②当CE平行于x轴,CD平行于y轴时,连接DE,若△CDE的面积为,请直接写出点C的坐标.
【分析】(1)将点A的坐标代入直线y=kx+4(k≠0) 即可算出k的值,从而求出一次函数的解析式;(2) ① 根据直线与y轴交点的坐标特点,求出点B的坐标,从而得出OB的长度,根据中点的定义得出BE=OE=2,根据平行四边形的对边平行得出 CE∥DA, 根据平行线分线段成比例定理得出,所以点C是AB的中点, 进而根据三角形的中位线定理得出 CE=OA=4, 在Rt△DOE中 ,利用勾股定理算出DE长,从而根据平行四边形周长的计算方法即可算出答案; ② 根据点的坐标与图形的性质设出点C的坐标,然后根据三角形的面积计算方法,由△CDE的面积为建立方程,求解即可得出x的值,从而求出点C的坐标.
【解答】 (1)将A(8,0)代入y=kx+4,得:0=8k+4,
解得:.
(2)①由(1)可知直线AB的解析式为.
当x=0时,,
∴点B的坐标为(0,4),
∴OB=4.
∵点E为OB的中点,
∴BE=OE=OB=2.
∵点A的坐标为(8,0),
∴OA=8.
∵四边形OCED是平行四边形,
∴CE∥DA,
∴ ,
∴BC=AC,
∴CE是△ABO的中位线,
∴CE=OA=4.
∵四边形OCED是平行四边形,
∴OD=CE=4,OC=DE.
在Rt△DOE中,∠DOE=90°,OD=4,OE=2,
∴DE== 2,
∴C平行四边形OCED=2(OD+DE)=2(4+2)=8+4.
②设点C的坐标为(x,x+4),则CE=|x|,CD=|x+4|,
∴S△CDE=CD•CE=|x2+2x|=,
∴x2+8x+33=0或x2+8x﹣33=0.
方程x2+8x+33=0无解;
解方程x2+8x﹣33=0,得:x1=﹣3,x2=11,
∴点C的坐标为(﹣3,)或(11,).
1.一次函数应用问题的求解思路:
建立一次函数模型→求出一次函数解析式→结合函数解析式、函数性质作出解答.
利用函数并与方程(组)、不等式(组)联系在一起解决实际生活中的利率、利润、租金、生产方案的设计问题以及经济决策、市场经济等方面的应用.
2.建立函数模型解决实际问题的一般步骤:
(1)审题,设定实际问题中的变量,明确变量x和y;
(2)根据等量关系,建立变量与变量之间的函数关系式,如:一次函数的函数关系式;
(3)确定自变量x的取值范围,保证自变量具有实际意义;
(4)利用函数的性质解决问题;
(5)写出答案.
3.利用一次函数的图象解决实际问题的一般步骤:
(1)观察图象,获取有效信息;
(2)对获取的信息进行加工、处理,理清各数量之间的关系;
(3)选择适当的数学工具(如函数、方程、不等式等),通过建模解决问题.
【提示】时刻注意根据实际情况确定变量的取值范围.
【例7】(2020•吉林23/26)某种机器工作前先将空油箱加满,然后停止加油立即开始工作.当停止工作时,油箱中油量为5L,在整个过程中,油箱里的油量y(单位:L)与时间x(单位:min)之间的关系如图所示.
(1)机器每分钟加油量为 L,机器工作的过程中每分钟耗油量为 L.
(2)求机器工作时y关于x的函数解析式,并写出自变量x的取值范围.
(3)直接写出油箱中油量为油箱容积的一半时x的值.
【考点】一次函数的应用
【分析】(1)根据函数图象中的数据,可以得到机器每分钟加油量和机器工作的过程中每分钟耗油量;
(2)根据函数图象中的数据,可以得到机器工作时y关于x的函数解析式,并写出自变量x的取值范围;
(3)根据(2)中的函数解析式,令函数值为30÷2,即可得到相应的x的值.
【解答】解:(1)由图象可得,
机器每分钟加油量为:30÷10=3(L),
机器工作的过程中每分钟耗油量为:(30-5)÷(60-10)=0.5(L),
故答案为:3,0.5;
(2)当10<x≤60时,设y关于x的函数解析式为y=ax+b,
,
解得:,
即机器工作时y关于x的函数解析式为y=-0.5 x +35(10<x≤60);
(3)当3x=30÷2时,得x =5,
当-0.5 x +35=30÷2时,得x =40,
即油箱中油量为油箱容积的一半时x的值是5或40.
【点评】本题考查一次函数的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
【例8】(2020•福建20/25)某公司经营甲、乙两种特产,其中甲特产每吨成本价为10万元,销售价为10.5万元;乙特产每吨成本价为1万元,销售价为1.2万元.由于受有关条件限制,该公司每月这两种特产的销售量之和都是100吨,且甲特产的销售量都不超过20吨.
(1)若该公司某月销售甲、乙两种特产的总成本为235万元,问这个月该公司分别销售甲、乙两种特产各多少吨?
(2)求该公司一个月销售这两种特产所能获得的最大总利润.
【考点】一元一次方程的应用;一次函数的应用
【分析】(1)根据题意,可以列出相应的一元一次方程,从而可以求得这个月该公司销售甲、乙两种特产分别为多少吨;
(2)根据题意,可以得到利润与甲种特产数量的函数关系式,再根据甲种特产的取值范围和一次函数的性质,可以得到利润的最大值.
【解答】解:(1)设销售甲种特产x吨,则销售乙种特产(100- x)吨,
10 x +(100- x)×1=235,
解得,x =15,
∴100- x =85,
答:这个月该公司销售甲、乙两种特产分别为15吨,85吨;
(2)设利润为w万元,销售甲种特产a吨,
w=(10.5-10)a+(1.2-1)×(100-a)=0.3a+20,
∵0≤a≤20,
∴当a=20时,w取得最大值,此时w =26,
答:该公司一个月销售这两种特产所能获得的最大总利润是26万元.
【点评】本题考查一次函数的应用、一元一次方程的应用,解答本题的关键是明确题意,利用一次函数的性质和方程的知识解答.
【例9】(2020•包头23/26)某商店销售A、B两种商品,A种商品的销售单价比B种商品的销售单价少40元,2件A种商品和3件B种商品的销售总额为820元.
(1)求A种商品和B种商品的销售单价分别为多少元?
(2)该商店计划购进A,B两种商品共60件,且A,B两种商品的进价总额不超过7800元.已知A种商品和B种商品的每件进价分别为110元和140元,应如何进货才能使这两种商品全部售出后总获利最多?
【考点】二元一次方程组的应用;一元一次不等式的应用;一次函数的应用.
【答案】见试题解答内容
【分析】(1)设A种商品的销售单价是x元,B种商品的销售单价是y元,根据A种商品的销售单价比B种商品的销售单价少40元,2件A种商品和3件B种商品的销售总额为820元列方程组,解出即可解答;
(2)根据不等量关系:A种商品总进价+B种商品总进价≤7800,列不等式,解出即可解答.
【解答】解:(1)设A种商品的销售单价是x元,B种商品的销售单价是y元
根据题意得:,
解得:,
答:A种商品的销售单价是140元,B种商品的销售单价是180元;
(2)设购进A种商品a件,则购进B种商品(60﹣a)件,设总获利为w元,
根据题意得:110a+140(60﹣a)≤7800,
解得:a≥20,
w=(140﹣110)a+(180﹣140)(60﹣a)=﹣10a+2400,
∵﹣10<0,
∴w随a的增大而减小,
∴当a=20时,w有最大值;
答:商店购进A种商品20件,购进B种商品40件时,总获利最多.
【点评】本题考查二元一次方程组,一次函数的性质,一元一次不等式的综合运用,重点掌握解应用题的步骤.难点是正确列出相等关系和不等量关系.
【例10】(2020•新疆兵团21/23)某超市销售A、B两款保温杯,已知B款保温杯的销售单价比A款保温杯多10元,用480元购买B款保温杯的数量与用360元购买A款保温杯的数量相同.
(1)A、B两款保温杯的销售单价各是多少元?
(2)由于需求量大,A、B两款保温杯很快售完,该超市计划再次购进这两款保温杯共120个,且A款保温杯的数量不少于B款保温杯数量的两倍.若A款保温杯的销售单价不变,B款保温杯的销售单价降低10%,两款保温杯的进价每个均为20元,应如何进货才能使这批保温杯的销售利润最大,最大利润是多少元?
【考点】分式方程的应用;一次函数的应用
【分析】(1)根据题意可以列出相应的分式方程,从而可以求得A、B两款保温杯的销售单价,注意分式方程要检验;
(2)根据题意可以得到利润与购买A款保温杯数量的函数关系,然后根据A款保温杯的数量不少于B款保温杯数量的两倍,可以求得A款保温杯数量的取值范围,再根据一次函数的性质,即可求得应如何进货才能使这批保温杯的销售利润最大,最大利润是多少元.
【解答】解:(1)设A款保温杯的单价是a元,则B款保温杯的单价是(a+10)元,
,
解得,a=30,
经检验,a=30是原分式方程的解,
则a+10=40,
答:A、B两款保温杯的销售单价分别是30元、40元;
(2)设购买A款保温杯x个,则购买B款保温杯(120-x)个,利润为w元,
w=(30-20) x+[40×(1-10%)-20]×(120-x)=-6x+1920,
∵A款保温杯的数量不少于B款保温杯数量的两倍,
∴x≥2(120-x),
解得,x≥80,
∴当x=80时,w取得最大值,此时w=1440,120-x=40,
答:当购买A款保温杯80个,B款保温杯40个时,能使这批保温杯的销售利润最大,最大利润是1440元.
【点评】本题考查分式方程的应用、一次函数的应用,解答本题的关键是明确题意,利用一次函数的性质和分式方程的知识解答,注意分式方程要检验.
1.(2019·杭州)某函数满足当自变量x=1时,函数值y=0;当自变量x=0时,函数值y=1.写出一个满足条件的函数表达式________.
2.(2019·江西)如图,在平面直角坐标系中,点A,B的坐标分别为(,0) , (,1) ,连接AB,以AB为边向上作等边三角形ABC.
(1)求点C的坐标;
(2)求线段BC所在直线的解析式.
3.(2019•鄂尔多斯15/24)如图,有一条折线A1B1A2B2A3B3A4B4…,它是由过A1(0,0),B1(4,4),A2(8,0)组成的折线依次平移8,16,24,…个单位得到的,直线y=kx+2与此折线有2n(n≥1且为整数)个交点,则k的值为 .
4.(2019•赤峰24/26)阅读下面材料:
我们知道一次函数y=kx+b(k≠0,k、b是常数)的图象是一条直线,到高中学习时,直线通常写成Ax+By+C=0(A≠0,A、B、C是常数)的形式,点P(x0,y0)到直线Ax+By+C=0的距离可用公式d=计算.
例如:求点P(3,4)到直线y=﹣2x+5的距离.
解:∵y=﹣2x+5
∴2x+y﹣5=0,其中A=2,B=1,C=﹣5
∴点P(3,4)到直线y=﹣2x+5的距离为:
d====
根据以上材料解答下列问题:
(1)求点Q(﹣2,2)到直线3x﹣y+7=0的距离;
(2)如图,直线y=﹣x沿y轴向上平移2个单位得到另一条直线,求这两条平行直线之间的距离.
5.(2020•鄂尔多斯10/24)鄂尔多斯动物园内的一段线路如图1所示,动物园内有免费的班车,从入口处出发,沿该线路开往大象馆,途中停靠花鸟馆(上下车时间忽略不计),第一班车上午9:20发车,以后每隔10分钟有一班车从入口处发车,且每一班车速度均相同.小聪周末到动物园游玩,上午9点到达入口处,因还没到班车发车时间,于是从入口处出发,沿该线路步行25分钟后到达花鸟馆,离入口处的路程y(米)与时间x(分)的函数关系如图2所示,下列结论错误的是( )
A.第一班车离入口处的距离y(米)与时间x(分)的解析式为y=200x﹣4000(20≤x≤38)
B.第一班车从入口处到达花鸟馆所需的时间为10分钟
C.小聪在花鸟馆游玩40分钟后,想坐班车到大象馆,则小聪最早能够坐上第四班车
D.小聪在花鸟馆游玩40分钟后,如果坐第五班车到大象馆,那么比他在花鸟馆游玩结束后立即步行到大象馆提前了7分钟(假设小聪步行速度不变)
6.(2020•天津23/25)在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.
已知小亮所在学校的宿舍、食堂、图书馆依次在同一条直线上,食堂离宿舍,图书馆离宿舍.周末,小亮从宿舍出发,匀速走了到食堂;在食堂停留吃早餐后,匀速走了到图书馆;在图书馆停留借书后,匀速走了返回宿舍.给出的图象反映了这个过程中小亮离宿舍的距离与离开宿舍的时间之间的对应关系.
请根据相关信息,解答下列问题:
(Ⅰ)填表:
离开宿舍的时间 | 2 | 5 | 20 | 23 | 30 |
离宿舍的距离 | 0.2 |
| 0.7 |
|
|
(Ⅱ)填空:
①食堂到图书馆的距离为 ;
②小亮从食堂到图书馆的速度为 ;
③小亮从图书馆返回宿舍的速度为 ;
④当小亮离宿舍的距离为时,他离开宿舍的时间为 .
(Ⅲ)当时,请直接写出关于的函数解析式.
7.(2020•陕西21/25)某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度与生长时间(天之间的关系大致如图所示.
(1)求与之间的函数关系式;
(2)当这种瓜苗长到大约时,开始开花结果,试求这种瓜苗移至大棚后.继续生长大约多少天,开始开花结果?
8.(2020•河北24/26)表格中的两组对应值满足一次函数,现画出了它的图象为直线,如图.而某同学为观察,对图象的影响,将上面函数中的与交换位置后得另一个一次函数,设其图象为直线.
0 | ||
1 |
(1)求直线的解析式;
(2)请在图上画出直线(不要求列表计算),并求直线被直线和轴所截线段的长;
(3)设直线与直线,及轴有三个不同的交点,且其中两点关于第三点对称,直接写出的值.
9.(2020•宁夏24/26)“低碳生活,绿色出行”是一种环保、健康的生活方式,小丽从甲地匀速步行前往乙地,同时,小明从乙地沿同一路线匀速步行前往甲地,两人之间的距离与步行时间之间的函数关系式如图中折线段所示.
(1)小丽与小明出发 相遇;
(2)在步行过程中,若小明先到达甲地.
①求小丽和小明步行的速度各是多少?
②计算出点的坐标,并解释点的实际意义.
10.(2020•重庆A卷17/26),两地相距,甲货车从地以的速度匀速前往地,到达地后停止.在甲出发的同时,乙货车从地沿同一公路匀速前往地,到达地后停止.两车之间的路程与甲货车出发时间之间的函数关系如图中的折线所示.其中点的坐标是,点的坐标是,则点的坐标是 .
11.(2020•重庆B卷17/26)周末,自行车骑行爱好者甲、乙两人相约沿同一路线从地出发前往地进行骑行训练,甲、乙分别以不同的速度匀速骑行,乙比甲早出发5分钟.乙骑行25分钟后,甲以原速的继续骑行,经过一段时间,甲先到达地,乙一直保持原速前往地.在此过程中,甲、乙两人相距的路程(单位:米)与乙骑行的时间(单位:分钟)之间的关系如图所示,则乙比甲晚 分钟到达地.
12.(2020•上海16/25)小明从家步行到学校需走的路程为1800米.图中的折线反映了小明从家步行到学校所走的路程(米与时间(分钟)的函数关系,根据图象提供的信息,当小明从家出发去学校步行15分钟时,到学校还需步行 米.
13.(2020•河南19/23)暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.
设某学生暑期健身(次,按照方案一所需费用为(元,且;按照方案二所需费用为(元,且.其函数图象如图所示.
(1)求和的值,并说明它们的实际意义;
(2)求打折前的每次健身费用和的值;
(3)八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说明理由.
14.(2019·天津)甲、乙两个批发店销售同一种苹果,在甲批发店,不论一次购买数量是多少,价格均为6元/千克,在乙批发店,一次购买数量不超过50千克时,价格为7元/千克;一次购买数量超过50千克时,其中有50千克的价格仍为7元/千克,超出50千克部分的价格为5元/千克.设小王在同一个批发店一次购买苹果的数量为x千克(x>0).
(1)根据题意填表:
一次购买数量/千克 | 30 | 50 | 150 | … |
甲批发店花费/元 |
| 300 |
| … |
乙批发店花费/元 |
| 350 |
| … |
(2)设在甲批发店花费y1元,在乙批发店花费y2元,分别求y1,y2关于x的函数解析式;
(3)根据题意填空:
①若小王在甲批发店和在乙批发店一次购买苹果的数量相同,且花费相同,则他在同一个批发店一次购买苹果的数量为 千克;
②若小王在同一个批发店一次购买苹果的数量为120千克,则他在甲、乙两个批发店中的 批发店购买花费少;
③若小王在同一个批发店一次购买苹果花费了360元,则他在甲、乙两个批发店中的 批发店购买数量多.
15.(2019·河北)长为300 m的春游队伍,以v(m/s)的速度向东行进.如图11-5①和图②,当队伍排尾行进到位置O时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为2v(m/s),当甲返回排尾后,他及队伍均停止行进,设排尾从位置O开始行进的时间为t(s),排头与O的距离为S头(m).
(1)当v=2时,解答:
①求S头与t的函数关系式(不写t的取值范围);
②当甲赶到排头位置时,求S头的值;在甲从排头返回到排尾过程中,设甲与位置O的距离为S甲(m),求S甲与t的函数关系式(不写t的取值范围).
(2)设甲这次往返队伍的总时间为T(s),求T与v的函数关系式(不写v的取值范围),并写出队伍在此过程中行进的路程.
16.(2019·恩施)某县有A、B两个大型蔬菜基地,共有蔬菜700吨.若将A基地的蔬菜全部运往甲市所需费用与B基地的蔬菜全部运往甲市所需费用相同.从A、B两基地运往甲、乙两市的运费单价如下表:
| 甲市(元/吨) | 乙市(元/吨) |
A基地 | 20 | 25 |
B基地 | 15 | 24 |
(1)求A、B两个蔬菜基地各有蔬菜多少吨?
(2)现甲市需要蔬菜260吨,乙市需要蔬菜440吨.设从A基地运送m吨蔬菜到甲市,请问怎样调运可使总运费最少?
17.(2019·深圳)有A,B两个发电厂,每焚烧一吨垃圾,A发电厂比B发电厂多发40度电,A焚烧20吨垃圾比B焚烧30吨垃圾少1800度电.
(1)求焚烧1吨垃圾,A和B各发电多少?
(2)A,B两个发电厂共焚烧90吨的垃圾,A焚烧的垃圾不多于B焚烧的垃圾两倍,求A厂和B厂总发电量最大为多少度?
18.(2019·雅安)某超市计划购进甲、乙两种商品,两种商品的进价、售价如下表:
商品 | 甲 | 乙 |
进价(元/件) | x+60 | x |
售价(元/件) | 200 | 100 |
若用360元购进甲种商品的件数与用180元购进乙种商品的件数相同.
(1)求甲、乙两种商品的进价是多少元?
(2)若超市销售甲、乙两种商品共50件,其中销售甲种商品为a件(a≥30),设销售完50件甲、乙两种商品的总利润为w元,求w与a之间的函数关系式,并求出w的最小值.
19.(2019·内江)某商店准备购进A,B两种商品,A种商品毎件的进价比B种商品每件的进价多20元,用3000元购进A种商品和用1800元购进B种商品的数量相同.商店将A种商品每件的售价定为80元,B种商品每件的售价定为45元.
(1)A种商品每件的进价和B种商品每件的进价各是多少元?
(2)商店计划用不超过1560元的资金购进A,B两种商品共40件,其中A种商品的数量不低于B种商品数量的一半,该商店有几种进货方案?
(3)端午节期间,商店开展优惠促销活动,决定对每件A种商品售价优惠m(10<m<20)元,B种商品售价不变,在(2)条件下,请设计出销售这40件商品获得总利润最大的进货方案.
20.(2019·河南省20/23)学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买3个A奖品和2个B奖品共需120元;购买5个A奖品和4个B奖品共需210元.
(1)求A,B两种奖品的单价;
(2)学校准备购买A,B两种奖品共30个,且A奖品的数量不少于B奖品数量的.请设计出最省钱的购买方案,并说明理由.
1.(2019·杭州)某函数满足当自变量x=1时,函数值y=0;当自变量x=0时,函数值y=1.写出一个满足条件的函数表达式________.
【答案】 y=-x+1或y=-x2+1或y=|x-1|等.
【解答】解:设函数表达式为y=kx+b,
∵x=1时,y=0;x=0时,y=1,
∴ ,
解得: ,
∴满足条件得函数表达式为:y=-x+1.
故答案为:y=-x+1.
2.(2019·江西)如图,在平面直角坐标系中,点A,B的坐标分别为(,0) , (,1) ,连接AB,以AB为边向上作等边三角形ABC.
(1)求点C的坐标;
(2)求线段BC所在直线的解析式.
【答案】 (1)解:如图,过点B作BH⊥x轴,
∵点A坐标为(,0) ,点B坐标为(,1),
∴|AB|==2 ,
∵ BH=1,
∴sin∠BAH== ,
∴∠BAH=30°,
∵ △ABC为等边三角形,
∴ AB=AC=2,
∴ ∠CAB=∠BAH=90°,
∴点C的纵坐标为2,
∴点C 的坐标为(,2).
(2)解:由(1)知点C 的坐标为(,2),点B的坐标为(,1),设直线BC的解析式为:y=kx+b,
则 ,解得 ,
故直线BC的函数解析式为y=x+.
3.(2019•鄂尔多斯15/24)如图,有一条折线A1B1A2B2A3B3A4B4…,它是由过A1(0,0),B1(4,4),A2(8,0)组成的折线依次平移8,16,24,…个单位得到的,直线y=kx+2与此折线有2n(n≥1且为整数)个交点,则k的值为 .
【解答】解:∵A1(0,0),A2(8,0),A3(16,0),A4(24,0),…,
∴An(8n﹣8,0).
∵直线y=kx+2与此折线恰有2n(n≥1且为整数)个交点,
∴点An+1(8n,0)在直线y=kx+2上,
∴0=8nk+2,
解得:k=﹣.
故答案为:﹣.
4.(2019•赤峰24/26)阅读下面材料:
我们知道一次函数y=kx+b(k≠0,k、b是常数)的图象是一条直线,到高中学习时,直线通常写成Ax+By+C=0(A≠0,A、B、C是常数)的形式,点P(x0,y0)到直线Ax+By+C=0的距离可用公式d=计算.
例如:求点P(3,4)到直线y=﹣2x+5的距离.
解:∵y=﹣2x+5
∴2x+y﹣5=0,其中A=2,B=1,C=﹣5
∴点P(3,4)到直线y=﹣2x+5的距离为:
d====
根据以上材料解答下列问题:
(1)求点Q(﹣2,2)到直线3x﹣y+7=0的距离;
(2)如图,直线y=﹣x沿y轴向上平移2个单位得到另一条直线,求这两条平行直线之间的距离.
【考点】分母有理化;一次函数的性质;一次函数图象与几何变换;两条直线相交或平行问题.
【分析】(1)直接将Q点的坐标代入公式d=就可以求出结论;
(2)在直线y=﹣x任意取一点P,求出P点的坐标,然后代入点到直线y=﹣x+2的距离公式d=就可以求出结论.
【解答】解:(1)∵3x﹣y+7=0,
∴A=3,B=﹣1,C=7.
∵点Q(﹣2,2),
∴d===.
∴点Q(﹣2,2)到到直线3x﹣y+7=0的距离为;
(2)直线y=﹣x沿y轴向上平移2个单位得到另一条直线为y=﹣x+2,
在直线y=﹣x上任意取一点P,
当x=0时,y=0.
∴P(0,0).
∵直线y=﹣x+2,
∴A=1,B=1,C=﹣2
∴d==,
∴两平行线之间的距离为.
【点评】本题考查了一次函数的点与直线之间的距离公式的运用,由函数的解析式求点的坐标的运用,平行线的性质的运用,解答时掌握点到直线的距离公式是关键.
5.(2020•鄂尔多斯10/24)鄂尔多斯动物园内的一段线路如图1所示,动物园内有免费的班车,从入口处出发,沿该线路开往大象馆,途中停靠花鸟馆(上下车时间忽略不计),第一班车上午9:20发车,以后每隔10分钟有一班车从入口处发车,且每一班车速度均相同.小聪周末到动物园游玩,上午9点到达入口处,因还没到班车发车时间,于是从入口处出发,沿该线路步行25分钟后到达花鸟馆,离入口处的路程y(米)与时间x(分)的函数关系如图2所示,下列结论错误的是( )
A.第一班车离入口处的距离y(米)与时间x(分)的解析式为y=200x﹣4000(20≤x≤38)
B.第一班车从入口处到达花鸟馆所需的时间为10分钟
C.小聪在花鸟馆游玩40分钟后,想坐班车到大象馆,则小聪最早能够坐上第四班车
D.小聪在花鸟馆游玩40分钟后,如果坐第五班车到大象馆,那么比他在花鸟馆游玩结束后立即步行到大象馆提前了7分钟(假设小聪步行速度不变)
【考点】一次函数的应用.
【答案】C
【分析】设y=kx+b,运用待定系数法求解即可得出第一班车离入口处的距离y(米)与时间x(分)的解析式;把y=2500代入函数解析式即可求出第一班车从入口处到达花鸟馆所需的时间;设小聪坐上了第n班车,30﹣25+10(n﹣1)≥40,解得n≥4.5,可得小聪坐上了第5班车,再根据“路程、速度与时间的关系”解答即可.
【解答】解:由题意得,可设第一班车离入口处的距离y(米)与时间x(分)的解析式为:y=kx+b(k≠0),
把(20,0),(38,3600)代入y=kx+b,得,解得,
∴第一班车离入口处的路程y(米)与时间x(分)的函数表达为y=200x﹣4000(20≤x≤38);
故选项A不合题意;
把y=2000代入y=200x﹣4000,解得x=30,
30﹣20=10(分),
∴第一班车从入口处到达塔林所需时间10分钟;
故选项B不合题意;
设小聪坐上了第n班车,则
30﹣25+10(n﹣1)≥40,解得n≥4.5,
∴小聪坐上了第5班车,
故选项C符合题意;
等车的时间为5分钟,坐班车所需时间为:1600÷200=8(分),
步行所需时间:1600÷(2000÷25)=20(分),
20﹣(8+5)=7(分),
∴比他在花鸟馆游玩结束后立即步行到大象馆提前了7分钟.
故选项D不合题意.
故选:C.
【点评】本题主要考查了一次函数的应用,熟练掌握待定系数法求出函数解析式是解答本题的关键.
6.(2020•天津23/25)在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.
已知小亮所在学校的宿舍、食堂、图书馆依次在同一条直线上,食堂离宿舍,图书馆离宿舍.周末,小亮从宿舍出发,匀速走了到食堂;在食堂停留吃早餐后,匀速走了到图书馆;在图书馆停留借书后,匀速走了返回宿舍.给出的图象反映了这个过程中小亮离宿舍的距离与离开宿舍的时间之间的对应关系.
请根据相关信息,解答下列问题:
(Ⅰ)填表:
离开宿舍的时间 | 2 | 5 | 20 | 23 | 30 |
离宿舍的距离 | 0.2 |
| 0.7 |
|
|
(Ⅱ)填空:
①食堂到图书馆的距离为 ;
②小亮从食堂到图书馆的速度为 ;
③小亮从图书馆返回宿舍的速度为 ;
④当小亮离宿舍的距离为时,他离开宿舍的时间为 .
(Ⅲ)当时,请直接写出关于的函数解析式.
【考点】一次函数的应用
【分析】(Ⅰ)根据题意和函数图象,可以将表格补充完整;
(Ⅱ)根据函数图象中的数据,可以将各个小题中的空补充完整;
(Ⅲ)根据(Ⅱ)中的结果和函数图象中的数据,可以写出当时,关于的函数解析式.
【解答】解:(Ⅰ)由图象可得,
在前7分钟的速度为,
故当时,离宿舍的距离为,
在时,距离不变,都是,故当时,离宿舍的距离为,
在时,距离不变,都是,故当时,离宿舍的距离为,
故答案为:0.5,0.7,1;
(Ⅱ)由图象可得,
①食堂到图书馆的距离为,
故答案为:0.3;
②小亮从食堂到图书馆的速度为:,
故答案为:0.06;
③小亮从图书馆返回宿舍的速度为:,
故答案为:0.1;
④当时,
小亮离宿舍的距离为时,他离开宿舍的时间为,
当时,
小亮离宿舍的距离为时,他离开宿舍的时间为,
故答案为:6或62;
(Ⅲ)由图象可得,
当时,;
当时,;
当时,设,
,得,
即当时,;
由上可得,当时,关于的函数解析式是.
【点评】本题考查一次函数的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
7.(2020•陕西21/25)某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术.这种瓜苗早期在农科所的温室中生长,长到大约时,移至该村的大棚内,沿插杆继续向上生长.研究表明,60天内,这种瓜苗生长的高度与生长时间(天之间的关系大致如图所示.
(1)求与之间的函数关系式;
(2)当这种瓜苗长到大约时,开始开花结果,试求这种瓜苗移至大棚后.继续生长大约多少天,开始开花结果?
【考点】一次函数的应用
【分析】(1)分段函数,利用待定系数法解答即可;
(2)利用(1)的结论,把代入求出的值即可解答.
【解答】解:(1)当时,设,
则:,
解得,
;
当时,设,
则:,
解得,
,
;
(2)当时,,解得,
(天,
这种瓜苗移至大棚后.继续生长大约18天,开始开花结果.
【点评】本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,已知函数值求自变量的值,仔细观察图象,准确获取信息是解题的关键.
8.(2020•河北24/26)表格中的两组对应值满足一次函数,现画出了它的图象为直线,如图.而某同学为观察,对图象的影响,将上面函数中的与交换位置后得另一个一次函数,设其图象为直线.
0 | ||
1 |
(1)求直线的解析式;
(2)请在图上画出直线(不要求列表计算),并求直线被直线和轴所截线段的长;
(3)设直线与直线,及轴有三个不同的交点,且其中两点关于第三点对称,直接写出的值.
【考点】一次函数的性质;一次函数的图象;一次函数图象与几何变换
【分析】(1)根据待定系数法求得即可;
(2)画出直线,求得两直线的交点,根据勾股定理即可求得直线被直线和轴所截线段的长;
(3)求得两条直线与直线的交点横坐标,分三种情况讨论求得即可.
【解答】解:(1)直线中,当时,;当时,,
,解得,
直线的解析式为;
(2)依题意可得直线的解析式为
如图,
解得,
两直线的交点为,
直线与轴的交点为,
直线被直线和轴所截线段的长为:;
(3)把代入得,,解得;
把代入得,,解得;
分三种情况:①当第三点在轴上时,,
解得;
②当第三点在直上时,,
解得;
③当第三点在直线上时,,
解得;
直线与直线,及轴有三个不同的交点,且其中两点关于第三点对称,则的值为或7或.
【点评】本题考查了一次函数图象与几何变换,两直线相交问题,待定系数法求一次函数的解析式,分类讨论是解题的关键.
9.(2020•宁夏24/26)“低碳生活,绿色出行”是一种环保、健康的生活方式,小丽从甲地匀速步行前往乙地,同时,小明从乙地沿同一路线匀速步行前往甲地,两人之间的距离与步行时间之间的函数关系式如图中折线段所示.
(1)小丽与小明出发 相遇;
(2)在步行过程中,若小明先到达甲地.
①求小丽和小明步行的速度各是多少?
②计算出点的坐标,并解释点的实际意义.
【考点】一次函数的应用
【分析】(1)直接从图象获取信息即可;
(2)①设小丽步行的速度为,小明步行的速度为,且,根据图象和题意列出方程组,求解即可;
②设点的坐标为,根据题意列出方程解出,再根据图象求出即可,再结合两人的运动过程解释点的意义即可.
【解答】解:(1)由图象可得小丽与小明出发相遇,
故答案为:30;
(2)①设小丽步行的速度为,小明步行的速度为,且,
则,
解得:,
答:小丽步行的速度为,小明步行的速度为;
②设点的坐标为,
则可得方程,
解得,,
点,
点表示:两人出发时,小明到达甲地,此时两人相距.
【点评】本题考查了二元一次方程组的实际应用,一元一次方程的实际应用,从图象获取信息是解题关键.
10.(2020•重庆A卷17/26),两地相距,甲货车从地以的速度匀速前往地,到达地后停止.在甲出发的同时,乙货车从地沿同一公路匀速前往地,到达地后停止.两车之间的路程与甲货车出发时间之间的函数关系如图中的折线所示.其中点的坐标是,点的坐标是,则点的坐标是 .
【考点】一次函数的应用
【分析】根据点与点的坐标即可得出乙货车的速度,进而得出乙货车从地到地所用时间,据此即可得出点的坐标.
【解答】解:根据题意可得,乙货车的速度为:,
乙货车从地到地所用时间为:(小时),
当乙货车到底地时,甲货车行驶的路程为:(千米),
点的坐标是.
故答案为:.
【点评】本题考查一次函数的应用,解题的关键是读懂图象信息,掌握路程、速度、时间之间的关系,属于中考常考题型.
11.(2020•重庆B卷17/26)周末,自行车骑行爱好者甲、乙两人相约沿同一路线从地出发前往地进行骑行训练,甲、乙分别以不同的速度匀速骑行,乙比甲早出发5分钟.乙骑行25分钟后,甲以原速的继续骑行,经过一段时间,甲先到达地,乙一直保持原速前往地.在此过程中,甲、乙两人相距的路程(单位:米)与乙骑行的时间(单位:分钟)之间的关系如图所示,则乙比甲晚 分钟到达地.
【考点】一次函数的应用
【分析】首先确定甲乙两人的速度,求出总里程,再求出甲到达地时,乙离地的距离即可解决问题.
【解答】解:由题意乙的速度为(米分),设甲的速度为米分.
则有:,
解得,
25分钟后甲的速度为(米分).
由题意总里程(米,
86分钟乙的路程为(米,
(分钟).
故答案为12.
【点评】本题考查一次函数的应用,解题的关键是读懂图象信息,灵活运用所学知识解决问题,属于中考填空题中的压轴题.
12.(2020•上海16/25)小明从家步行到学校需走的路程为1800米.图中的折线反映了小明从家步行到学校所走的路程(米与时间(分钟)的函数关系,根据图象提供的信息,当小明从家出发去学校步行15分钟时,到学校还需步行 米.
【考点】一次函数的应用
【分析】当时,设,将、代入求得,求出时的值,从而得出答案.
【解答】解:当时,设,
将、代入,得:
,
解得:,
;
当时,,
,
当小明从家出发去学校步行15分钟时,到学校还需步行350米,
故答案为:350.
【点评】本题主要考查一次函数的应用,解题的关键是理解题意,从实际问题中抽象出一次函数的模型,并熟练掌握待定系数法求一次函数的解析式.
13.(2020•河南19/23)暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.
设某学生暑期健身(次,按照方案一所需费用为(元,且;按照方案二所需费用为(元,且.其函数图象如图所示.
(1)求和的值,并说明它们的实际意义;
(2)求打折前的每次健身费用和的值;
(3)八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说明理由.
【考点】一次函数的应用
【分析】(1)把点,代入,得到关于和的二元一次方程组,求解即可;
(2)根据方案一每次健身费用按六折优惠,可得打折前的每次健身费用,再根据方案二每次健身费用按八折优惠,求出的值;
(3)将分别代入、关于的函数解析式,比较即可.
【解答】解:(1)过点,,
,解得,
表示的实际意义是:购买一张学生暑期专享卡后每次健身费用为15元,
表示的实际意义是:购买一张学生暑期专享卡的费用为30元;
(2)由题意可得,打折前的每次健身费用为(元,
则;
(3)选择方案一所需费用更少.理由如下:
由题意可知,,.
当健身8次时,
选择方案一所需费用:(元,
选择方案二所需费用:(元,
,
选择方案一所需费用更少.
【点评】本题考查了一次函数的应用,解题的关键是理解两种优惠活动方案,求出、关于的函数解析式.
14.(2019·天津)甲、乙两个批发店销售同一种苹果,在甲批发店,不论一次购买数量是多少,价格均为6元/千克,在乙批发店,一次购买数量不超过50千克时,价格为7元/千克;一次购买数量超过50千克时,其中有50千克的价格仍为7元/千克,超出50千克部分的价格为5元/千克.设小王在同一个批发店一次购买苹果的数量为x千克(x>0).
(1)根据题意填表:
一次购买数量/千克 | 30 | 50 | 150 | … |
甲批发店花费/元 |
| 300 |
| … |
乙批发店花费/元 |
| 350 |
| … |
(2)设在甲批发店花费y1元,在乙批发店花费y2元,分别求y1,y2关于x的函数解析式;
(3)根据题意填空:
①若小王在甲批发店和在乙批发店一次购买苹果的数量相同,且花费相同,则他在同一个批发店一次购买苹果的数量为 千克;
②若小王在同一个批发店一次购买苹果的数量为120千克,则他在甲、乙两个批发店中的 批发店购买花费少;
③若小王在同一个批发店一次购买苹果花费了360元,则他在甲、乙两个批发店中的 批发店购买数量多.
【答案】解:(1)一次购买30千克,不超过50千克,
∴在甲批发店花费180元,在乙批发店花费210元;
一次购买150千克,超过50千克,
∴在甲批发店花费900元,在乙批发店花费850元.
(2)y1=6x(x>0).
当0<x≤50时,y2=7x;当x>50时,y2=5x+100.
(3)①当y1=y2时,6x=5x+100,解得x=100.
②当x=120时,y1=6x=720;y2=5x+100=700.
∵720>700,∴在乙批发店购买花费少.
③当y1=360时,x=60;当y2=360时,x=52.
∵60>52,
∴在甲批发店购买数量多.
15.(2019·河北)长为300 m的春游队伍,以v(m/s)的速度向东行进.如图11-5①和图②,当队伍排尾行进到位置O时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为2v(m/s),当甲返回排尾后,他及队伍均停止行进,设排尾从位置O开始行进的时间为t(s),排头与O的距离为S头(m).
(1)当v=2时,解答:
①求S头与t的函数关系式(不写t的取值范围);
②当甲赶到排头位置时,求S头的值;在甲从排头返回到排尾过程中,设甲与位置O的距离为S甲(m),求S甲与t的函数关系式(不写t的取值范围).
(2)设甲这次往返队伍的总时间为T(s),求T与v的函数关系式(不写v的取值范围),并写出队伍在此过程中行进的路程.
【答案】解:(1)①排头走的路程为2t,则S头=2t+300.
②甲从排尾赶到排头时,有4t=2t+300.
解得t=150.
此时,S头=2×150+300=600(米).
S甲=600-4(t-150)=-4t+1200.
(2)设甲从排尾赶到排头用时为t1,
则2vt1=vt1+300,∴t1=.
设甲从排头返回到排尾用时为t2,
则t2=,
∴T=t1+t2=.
∴队伍行进的路程是T·v=·v=400(m).
16.(2019·恩施)某县有A、B两个大型蔬菜基地,共有蔬菜700吨.若将A基地的蔬菜全部运往甲市所需费用与B基地的蔬菜全部运往甲市所需费用相同.从A、B两基地运往甲、乙两市的运费单价如下表:
| 甲市(元/吨) | 乙市(元/吨) |
A基地 | 20 | 25 |
B基地 | 15 | 24 |
(1)求A、B两个蔬菜基地各有蔬菜多少吨?
(2)现甲市需要蔬菜260吨,乙市需要蔬菜440吨.设从A基地运送m吨蔬菜到甲市,请问怎样调运可使总运费最少?
【答案】 (1)解:设A、B两基地的蔬菜总量分别为x吨、y 吨.
根据题意得:,
解得: ,
答:A、B两基地的蔬菜总量分别为300吨和400吨.
(2)解:由题可知: ,
∴ 0≤m≤260
∵W=20m+25(300-m)+15(260-m)+24[400-(260-m)]
=4m+14760 .
∵4>0,
∴W随m的增大而增大,
∴ Wmin=14760.
答:当A基地运300吨到乙市,B基地运260吨到甲市,B基地运140吨到乙市时,总运费最少为14760元.
17.(2019·深圳)有A,B两个发电厂,每焚烧一吨垃圾,A发电厂比B发电厂多发40度电,A焚烧20吨垃圾比B焚烧30吨垃圾少1800度电.
(1)求焚烧1吨垃圾,A和B各发电多少?
(2)A,B两个发电厂共焚烧90吨的垃圾,A焚烧的垃圾不多于B焚烧的垃圾两倍,求A厂和B厂总发电量最大为多少度?
【答案】 (1)解:设焚烧1吨垃圾,A发电x度,B发电y度.
由题意得,解得.
答:焚烧1吨垃圾A和B各发电300度与260度.
(2)解:设A发电厂焚烧a吨垃圾,则B发电厂焚烧(90-a)吨垃圾,总发电量为W度.
由题意得:a≤2(90-a)
∴a≤60
W=300a+260(90-a)
=40a+23400
∵40>0
∴W随a的增大而增大
∴当a=60时,Wmax=25800
答:A厂和B厂总发电量最大为25800度.
18.(2019·雅安)某超市计划购进甲、乙两种商品,两种商品的进价、售价如下表:
商品 | 甲 | 乙 |
进价(元/件) | x+60 | x |
售价(元/件) | 200 | 100 |
若用360元购进甲种商品的件数与用180元购进乙种商品的件数相同.
(1)求甲、乙两种商品的进价是多少元?
(2)若超市销售甲、乙两种商品共50件,其中销售甲种商品为a件(a≥30),设销售完50件甲、乙两种商品的总利润为w元,求w与a之间的函数关系式,并求出w的最小值.
【答案】 (1)解:依题意可得方程:,
解得x=60,
经检验x=60是方程的根,
∴ x+60=120元,
答:甲、乙两种商品的进价分别是120元,60元.
(2)解:∵销售甲种商品为a件(a≥30),
∴销售乙种商品为(50-a)件,
根据题意得:w=(200-120)a+(100-60)(50-a)=40a+2000(a≥30),
∵ 40>0,
∴w的值随a值的增大而增大,
∴当a=30时,w最小值=40×30+2000=3200(元).
19.(2019·内江)某商店准备购进A,B两种商品,A种商品毎件的进价比B种商品每件的进价多20元,用3000元购进A种商品和用1800元购进B种商品的数量相同.商店将A种商品每件的售价定为80元,B种商品每件的售价定为45元.
(1)A种商品每件的进价和B种商品每件的进价各是多少元?
(2)商店计划用不超过1560元的资金购进A,B两种商品共40件,其中A种商品的数量不低于B种商品数量的一半,该商店有几种进货方案?
(3)端午节期间,商店开展优惠促销活动,决定对每件A种商品售价优惠m(10<m<20)元,B种商品售价不变,在(2)条件下,请设计出销售这40件商品获得总利润最大的进货方案.
【答案】 (1)解:设A种商品每件的进价是x元,则B种商品每件的进价是(x-20)元,
由题意得:,
解得:x=50,
经检验,x=50是原方程的解,且正确,
50-20=30,
答:A种商品每件的进价是50元,B种商品每件的进价是30元
(2)解:设购买A种商品a件,则购买B商品(40-a)件,
由题意得: ,
解得:≤a≤18,
∵a为正整数,
∴a=14、15、16、17、18,
∴商店共有5种进货方案;
(3)解:设销售A,B两种商品共获利y元,
由题意得:y=(80-50-m)a+(45-30)(40-a)
=(15-m)a+600,
①当10<m<15时,15-m>0,y随a的增大而增大,
∴当 a=18时,获利最大,即买18件 A 商品,22件B商品,
②当m=15时,15-m=0,
y与a的值无关,即(2)问中所有进货方案获利相同,
③当15<m<20时,15-m<0 ,y随a的增大而减小,
∴当 a=14时,获利最大,即买14件 A商品,26件B商品.
20.(2019·河南省20/23)学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买3个A奖品和2个B奖品共需120元;购买5个A奖品和4个B奖品共需210元.
(1)求A,B两种奖品的单价;
(2)学校准备购买A,B两种奖品共30个,且A奖品的数量不少于B奖品数量的.请设计出最省钱的购买方案,并说明理由.
【分析】(1)设A的单价为x元,B的单价为y元,根据题意列出方程组,即可求解;(2)设购买A奖品z个,则购买B奖品为(30﹣z)个,购买奖品的花费为W元,根据题意得到由题意可知,z≥(30﹣z),W=30z+15(30﹣z)=450+15z,根据一次函数的性质,即可求解;
【解答】解:(1)设A的单价为x元,B的单价为y元,
根据题意,得
,
∴,
∴A的单价30元,B的单价15元;
(2)设购买A奖品z个,则购买B奖品为(30﹣z)个,购买奖品的花费为W元,
由题意可知,z≥(30﹣z),
∴z≥,
W=30z+15(30﹣z)=450+15z,
当z=8时,W有最小值为570元,
即购买A奖品8个,购买B奖品22个,花费最少.
专题中考数学 一次函数的应用(课件): 这是一份专题中考数学 一次函数的应用(课件),共56页。
专题14 一次函数的应用(课件)-2023年中考数学一轮复习(全国通用): 这是一份专题14 一次函数的应用(课件)-2023年中考数学一轮复习(全国通用),共56页。
专题14 一次函数的应用(课件+学案)-备战2023年中考数学一轮复习专题精讲精练学案+课件(全国通用): 这是一份专题14 一次函数的应用(课件+学案)-备战2023年中考数学一轮复习专题精讲精练学案+课件(全国通用),文件包含专题14一次函数的应用学案含解析docx、专题14一次函数的应用课件pptx等2份课件配套教学资源,其中PPT共56页, 欢迎下载使用。













