初中数学苏科版七年级下册7.5 多边形的内角和与外角和练习

这是一份初中数学苏科版七年级下册7.5 多边形的内角和与外角和练习，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
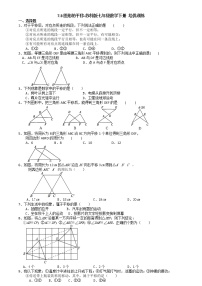
1、一个多边形的内角和是外角和的2倍．这个多边形的边数为（ ）
A．5B．6C．7D．8
2、下列说法正确的个数是（ ）
①七边形有14条对角线；②外角和大于内角和的多边形只有三角形；
③如果一个多边形的内角和与外角和的比是4:1，则它是九边形
A．0B．1C．2D．3
3、一个n边形的每一个外角等于其相邻内角的，则n的值为（ ）
A．6B．7C．8D．9
4、如图，小明从点出发，沿直线前进10米后向左转10°再沿直线前进10米后向左转20°再沿直线前进10米后向左转30°……照这样下去，他第一次回到出发地点时，一共走了（ ）
A．80米 B．160米 C．300米 D．640米

（4题） （6题） （7题）
5、若一个多边形的边数增加2倍，它的外角和( )
A．扩大2倍 B．缩小2倍C．保持不变D．无法确定
6、如图，∠1，∠2，∠3是五边形ABCDE的3个外角，若∠A+∠B＝220°，则∠1+∠2+∠3＝( )
A．140°B．180°C．220°D．320°
7、如图，七边形ABCDEFG中，AB，ED的延长线交于点O，若∠1，∠2，∠3，∠4的外角和等于215°，则∠BOD的度数为( )
A．20° B．35° C．40° D．45°
8、如图，∠A+∠B+∠C+∠D+∠E+∠F+∠AGF的度数是（ ）
A.360° B.540° C.720° D.无法确定

（8题） （9题） （17题）
9、如图,D、E、F分别是△ABC中边BC、AC、AB上的点,则∠1+∠2+∠3+∠4+∠5+∠6的度数是（ ）
A.180° B.240° C.360° D.540°
二、填空题
10、正十二边形的每一个外角等于________
11、如果一个多边形的内角和等于外角和的2倍，那么这个多边形的边数n=________
12、已知一个多边形的每一个外角都相等,一个内角与一个外角的度数之比为7:2,则这个多边形的边
数为_______
13、一个多边形的每一个外角等于36°，则该多边形的内角和等于_______
14、若一个多边形的内角和与外角和之和是1800°,则此多边形是 边形.
15、一个多边形边数增加1，则这个多边形内角增加 ，外角增加 .
16、若一个多边形的每一个外角都相等，它的一个外角等于一个内角的三分之二，
则这个多边形是_____边形．
17、如图，∠1、∠2、∠3、∠4是五边形ABCDE的4个外角．若∠A=120°，则∠1+∠2+∠3+∠4=__
18、一个n边形，除了一个内角外，其余（n-1）个内角和为2770°，则这个内角是_____
19、如图所示，求∠A+∠B+∠C+∠D+∠E+∠F的度数=________.

（19题） （20题）
20、如图，∠ADC＝117°，则∠A+∠B+∠C的度数为 ．
三、解答题
21、如图,在四边形ABCD中,∠B+∠D=180°,∠DCE是四边形ABCD的一个外角,∠DCE与∠A相等吗?
为什么?
22、如图，求∠A+∠B+∠C+∠D+∠E+∠F的度数和．
23、(1)一个多边形每个内角都相等，且每个外角等于一个内角的eq \f(2,3)，求这个多边形的边数；
(2)两个多边形边数之比为3∶4，内角和之比为2∶3，求这两个多边形的边数．
24、如图，在四边形ABCD中，∠F为四边形ABCD的∠ABC的平分线及外角∠DCE的平分线所在的直线构成的锐角，若设∠A＝α，∠D＝β.
（1）如图①，α＋β＞180°，试用α，β表示∠F；
（2）如图②，α＋β＜180°，请在图中画出∠F，并试用α，β表示∠F；
（3）一定存在∠F吗？如果一定存在，求出∠F的值；如果不一定存在，指出当α，β满足什么条件时，不存在∠F.
25、直线MN与直线PQ垂直相交于O，点A在射线OP上运动，点B在射线OM上运动．
（1）如图1，已知AE、BE分别是∠BAO和∠ABO角的平分线，点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值；
（2）如图2，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其延长线相交于E、F，则∠EAF＝ °；在△AEF中，如果有一个角是另一个角的3倍，试求∠ABO的度数．
26、如图①，在△ABC中，∠ABC与∠ACB的平分线相交于点P．
（1）如果∠A＝80°，求∠BPC的度数；
（2）如图②，作△ABC外角∠MBC，∠NCB的角平分线交于点Q，试探索∠Q、∠A之间的数量关系．
（3）如图③，延长线段BP、QC交于点E，△BQE中，存在一个内角等于另一个内角的2倍，
求∠A的度数．
7.5多边形的内角和与外角和（3）-苏科版七年级数学下册 培优训练（答案）
一、选择题
1、一个多边形的内角和是外角和的2倍．这个多边形的边数为（ B ）
A．5B．6C．7D．8
2、下列说法正确的个数是（ C ）
①七边形有14条对角线；②外角和大于内角和的多边形只有三角形；
③如果一个多边形的内角和与外角和的比是4:1，则它是九边形
A．0B．1C．2D．3
3、一个n边形的每一个外角等于其相邻内角的，则n的值为（ C ）
A．6B．7C．8D．9
4、如图，小明从点出发，沿直线前进10米后向左转10°再沿直线前进10米后向左转20°再沿直线前进10米后向左转30°……照这样下去，他第一次回到出发地点时，一共走了（ A ）
A．80米 B．160米 C．300米 D．640米

5、若一个多边形的边数增加2倍，它的外角和( C )
A．扩大2倍 B．缩小2倍C．保持不变D．无法确定
6、如图，∠1，∠2，∠3是五边形ABCDE的3个外角，若∠A+∠B＝220°，则∠1+∠2+∠3＝( C )
A．140°B．180°C．220°D．320°

7、如图，七边形ABCDEFG中，AB，ED的延长线交于点O，若∠1，∠2，∠3，∠4的外角和等于215°，则∠BOD的度数为( B )

A．20° B．35° C．40° D．45°
8、如图，∠A+∠B+∠C+∠D+∠E+∠F+∠AGF的度数是（ ）
A.360° B.540° C.720° D.无法确定

解答：解：在四边形BCDM中：∠C+∠B+∠D+∠2=360°，
在四边形MEFN中：∠1+∠3+∠E+∠F=360°．
∵∠1=∠A+∠G，∠2+∠3=180°，
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G=360°+360°-180°=540°．
故选B．

9、如图,D、E、F分别是△ABC中边BC、AC、AB上的点,则∠1+∠2+∠3+∠4+∠5+∠6的度数是（C ）
A.180° B.240° C.360° D.540°

二、填空题
10、正十二边形的每一个外角等于___30°_____
11、如果一个多边形的内角和等于外角和的2倍，那么这个多边形的边数n=_____6____
12、已知一个多边形的每一个外角都相等,一个内角与一个外角的度数之比为7:2,则这个多边形的边
数为____9____
13、一个多边形的每一个外角等于36°，则该多边形的内角和等于___1440°____
14、若一个多边形的内角和与外角和之和是1800°,则此多边形是 十 边形.
15、一个多边形边数增加1，则这个多边形内角增加 ，外角增加 .
答案180度，0度
16、若一个多边形的每一个外角都相等，它的一个外角等于一个内角的三分之二，则这个多边形是__ 正五___边形．
17、如图，∠1、∠2、∠3、∠4是五边形ABCDE的4个外角．若∠A=120°，则∠1+∠2+∠3+∠4=__ 300°

18、一个n边形，除了一个内角外，其余（n-1）个内角和为2770°，则这个内角是__110°____
19、如图所示，求∠A+∠B+∠C+∠D+∠E+∠F的度数=___360°_______.

20、如图，∠ADC＝117°，则∠A+∠B+∠C的度数为 ．

【解答】解：延长AD交BC于E，
∵∠AEC＝∠A+∠B，∠ADC＝∠AEC+∠C，∴∠ADC＝∠A+∠B+∠C，
∵∠ADC＝117°，∴∠A+∠B+∠C＝117°，故答案为：117°．

三、解答题
21、如图,在四边形ABCD中,∠B+∠D=180°,∠DCE是四边形ABCD的一个外角,∠DCE与∠A相等吗?
为什么?
解：∠DCE=∠A.
在四边形ABCD中,∠B+∠D=180°,所以∠A+∠BCD=180°.
因为∠DCE+∠BCD=180°，所以∠DCE=∠A.
22、如图，求∠A+∠B+∠C+∠D+∠E+∠F的度数和．
解： ∵∠APC是△AEP的外角，∴∠APC=∠A+∠E，
∵∠BOD是△DOF的外角，∴∠BOD=∠D+∠F，
∴∠A+∠B+∠C+∠D+∠E+∠F=∠B+∠C+∠APC+∠BOD=180°×（4-2）=360°．
23、(1)一个多边形每个内角都相等，且每个外角等于一个内角的eq \f(2,3)，求这个多边形的边数；
(2)两个多边形边数之比为3∶4，内角和之比为2∶3，求这两个多边形的边数．
解：(1)多边形的内角和是：360°×1.5＝540°.
设多边形的边数是n，则(n－2)·180°＝540°，解得n＝5.
故这个多边形的边数是5；
(2)∵两个多边形的边数之比为3∶4，
∴设一个多边形的边数为3n，则另一个为4n，
∵内角和度数之比为2∶3，∴(3n－2)∶(4n－2)＝2∶3，解得n＝2，
∴3n＝6，4n＝8.
故这两个多边形的边数分别为6和8.
24、如图，在四边形ABCD中，∠F为四边形ABCD的∠ABC的平分线及外角∠DCE的平分线所在的直线构成的锐角，若设∠A＝α，∠D＝β.
（1）如图①，α＋β＞180°，试用α，β表示∠F；
（2）如图②，α＋β＜180°，请在图中画出∠F，并试用α，β表示∠F；
（3）一定存在∠F吗？如果一定存在，求出∠F的值；如果不一定存在，指出当α，β满足什么条件时，不存在∠F.
（1）解：∵∠ABC＋∠DCB＝360°－(α＋β)，
∴∠ABC＋(180°－∠DCE)＝360°－(α＋β)＝2∠FBC＋(180°－2∠FCE)
＝180°－2(∠FCE－∠FBC)＝180°－2∠F.
∴360°－(α＋β)＝180°－2∠F，即2∠F＝α＋β－180°，
∴∠F＝eq \f(1,2)(α＋β)－90°.
（2）解：如答图，∵∠ABC＋∠DCB＝360°－(α＋β)，
∴∠ABC＋(180°－∠DCE)＝360°－(α＋β)
＝2∠GBC＋(180°－2∠HCE)＝180°＋2 (∠GBC－∠HCE)＝180°＋2∠F.
∴360°－(α＋β)＝180°＋2∠F， ∴∠F＝90°－eq \f(1,2)(α＋β)．
（3）解：当α＋β＝180°时，不存在∠F.

25、直线MN与直线PQ垂直相交于O，点A在射线OP上运动，点B在射线OM上运动．
（1）如图1，已知AE、BE分别是∠BAO和∠ABO角的平分线，点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值；
（2）如图2，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其延长线相交于E、F，则∠EAF＝ °；在△AEF中，如果有一个角是另一个角的3倍，试求∠ABO的度数．
【解答】解：（1）∠AEB的大小不变，
∵直线MN与直线PQ垂直相交于O，∴∠AOB＝90°，∴∠OAB+∠OBA＝90°，
∵AE、BE分别是∠BAO和∠ABO角的平分线，∴∠BAE＝∠OAB，∠ABE＝∠ABO，
∴∠BAE+∠ABE＝（∠OAB+∠ABO）＝×90°＝45°，∴∠AEB＝135°；
（2）∵AE、AF分别是∠BAO和∠OAG的角平分线，
∴∠EAO＝∠BAO，∠FAO＝∠GAO，∴∠EAF＝（∠BAO+∠GAO）＝×180°＝90°．
故答案为：90；
∵∠BAO与∠BOQ的角平分线相交于E，∴∠EAO＝∠BAO，∠EOQ＝∠BOQ，
∴∠E＝∠EOQ﹣∠EAO＝（∠BOQ﹣∠BAO）＝∠ABO，即∠ABO＝2∠E，
在△AEF中，∵有一个角是另一个角的3倍，故分四种情况讨论：
①∠EAF＝3∠E，∠E＝30°，则∠ABO＝60°；
②∠EAF＝3∠F，∠E＝60°，∠ABO＝120°（舍去）；
③∠F＝3∠E，∠E＝22.5°，∠ABO＝45°；
④∠E＝3∠F，∠E＝67.5°，∠ABO＝135°（舍去）．
∴∠ABO为60°或45°．
26、如图①，在△ABC中，∠ABC与∠ACB的平分线相交于点P．
（1）如果∠A＝80°，求∠BPC的度数；
（2）如图②，作△ABC外角∠MBC，∠NCB的角平分线交于点Q，试探索∠Q、∠A之间的数量关系．
（3）如图③，延长线段BP、QC交于点E，△BQE中，存在一个内角等于另一个内角的2倍，
求∠A的度数．
【解答】（1）解：∵∠A＝80°．∴∠ABC+∠ACB＝100°，
∵点P是∠ABC和∠ACB的平分线的交点，
∴∠P＝180°﹣（∠ABC+∠ACB）＝180°﹣×100°＝130°，
（2）∵外角∠MBC，∠NCB的角平分线交于点Q，
∴∠QBC+∠QCB＝（∠MBC+∠NCB）＝（360°﹣∠ABC﹣∠ACB）＝（180°+∠A）＝90°+∠A
∴∠Q＝180°﹣（90°+∠A）＝90°﹣∠A；
（3）∵CQ为△ABC的外角∠NCB的角平分线，∴CE是△ABC的外角∠ACF的平分线，
∴∠ACF＝2∠ECF，
∵BE平分∠ABC，∴∠ABC＝2∠EBC，
∵∠ECF＝∠EBC+∠E，∴2∠ECF＝2∠EBC+2∠E，即∠ACF＝∠ABC+2∠E，
又∵∠ACF＝∠ABC+∠A，∴∠A＝2∠E，即∠E＝∠A；
∵∠EBQ＝∠EBC+∠CBQ＝∠ABC+∠MBC＝（∠ABC+∠A+∠ACB）＝90°．
如果△BQE中，存在一个内角等于另一个内角的2倍，那么分四种情况：
①∠EBQ＝2∠E＝90°，则∠E＝45°，∠A＝2∠E＝90°；
②∠EBQ＝2∠Q＝90°，则∠Q＝45°，∠E＝45°，∠A＝2∠E＝90°；
③∠Q＝2∠E，则90°﹣∠A＝∠A，解得∠A＝60°；
④∠E＝2∠Q，则∠A＝2（90°﹣∠A），解得∠A＝120°．
综上所述，∠A的度数是90°或60°或120°．