小学数学人教版六年级下册圆柱的体积教案

这是一份小学数学人教版六年级下册圆柱的体积教案，文件包含人教版六下数学第三单元4圆柱的体积教案PPTpptx、人教版六下数学第三单元5圆柱的体积计算公式的拓展应用教案PPTpptx、人教版六下数学第三单元6圆柱的体积练习课教案PPTpptx等3份教案配套教学资源，其中教案共0页， 欢迎下载使用。

使学生能够运用公式正确地计算圆柱的体积和容积。初步学会用转化的数学思想和方法，解决实际问题的能力。渗透转化思想，培养学生的自主探索意识。
圆柱的体积公式是怎样推导的?圆柱的体积怎么求？长方体和正方体的体积怎么求?
 回顾问题，再现新知
1.教材第28页练习五第2题。 如图，这个圆柱形水桶可以装多少水？
 指导练习 ——基础练习
这是要求圆柱形水桶的体积还是表面积？
2.教材第28页练习五第3题。 学校建了两个同样大小的圆柱形花坛，花坛的底面内直径为3cm，高为0.8cm。如果里面填土的高度是0.5cm，两个花坛中共需要填土多少立方米？
0.8m这个条件有用吗？
0.8m为多余条件，要选择有用的条件解决问题。
3.教材第28页练习五第4题。 一个圆柱的体积是80cm³，底面是16cm²。它的高是多少厘米？
根据圆柱的体积公式，如果知道圆柱的体积和底面积，怎样求高？
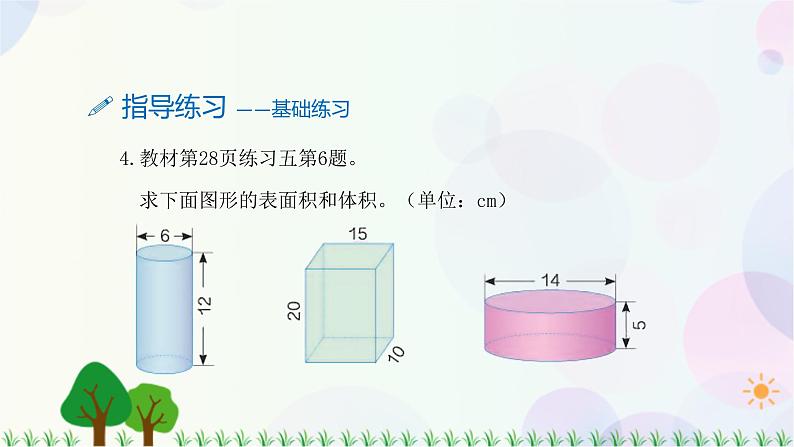
4.教材第28页练习五第6题。 求下面图形的表面积和体积。（单位：cm）
1.教材第28页练习五第5题。 一个圆柱形粮囤，从里面量得底面半径为1.5m，高2m。如果每立方米玉米约重750kg，这个粮囤能装多少吨玉米？要求：①粮囤能装多少吨玉米？ ②求粮囤的体积。
 指导练习 ——提高练习
2.教材第29页练习五第7题。 学校要在教学区和操场之间修一道围墙，原计划用土石35m³。后来多开了一个厚度为25cm的月亮门，减少了土石的用量。现在用了多少立方米土石？
3.教材第29页练习五第9题。 两个底面积相等的圆柱，一个高为4.5dm，体积为81dm³。另一个高为3dm，它的体积是多少？
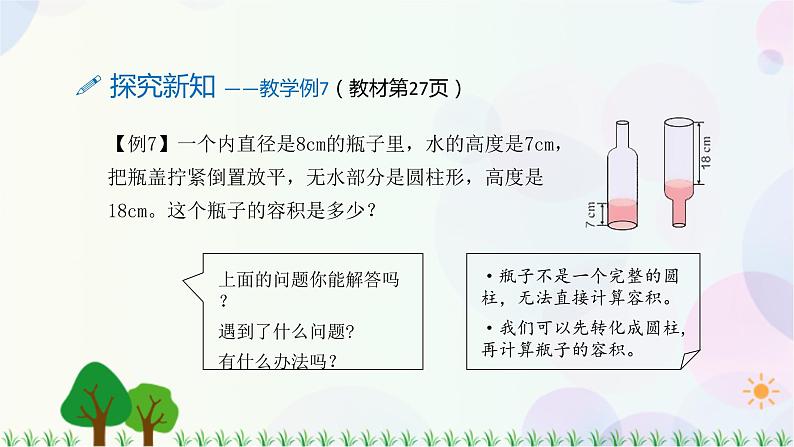
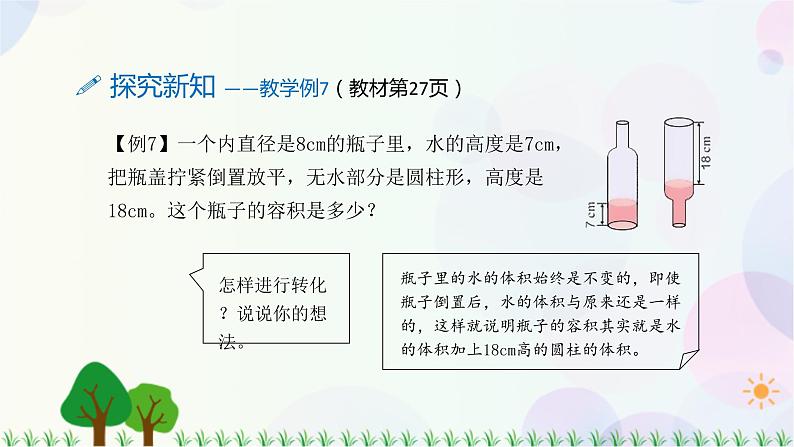
4.教材第29页练习五第10题。 一个圆柱形玻璃容器的底面直径是10cm，把一块完全浸在这个容器水中的铁块取出后，水面下降2cm。这块铁块的体积是多少？
要求铁块的体积，实际上就是要求下降部分水的体积，即相当于求底面直径10cm、高2cm的圆柱的体积
1.教材第29页练习五第12题。 下面是一根钢管，求它所用钢材的体积。
 指导练习 ——巩固练习
钢管的体积就是大圆柱的体积减去中空的小圆柱的体积。
2.教材第29页练习五第13题。 小雨家有6个从里面量得底面积是30cm³，高10cm的圆柱形水杯，沏一壶茶水能倒满4杯。有一天来了6位客人，如果让这6位客人都能喝上这壶茶水，平均每杯倒多少毫升？
此题的解题步骤应该是怎样的？先求算什么？再求算什么？最后求算什么？
先计算每个水杯的容积，再计算水的总体积，最后计算六个杯子中每杯应倒多少毫升水。
3.教材第30页练习五第14题。 右面这个长方形的长是20cm，宽是10cm。分别以长和宽为轴旋转一周，得到两个圆柱体。它们的体积各是多少？
3.教材第30页练习五第14题。
若以长为轴旋转一周，那么得到的圆柱和这个长方形有什么联系？
圆柱的高等于长方形的长，圆柱的底面半径等于长方形的宽。
如果以宽为轴旋转一周，那么得到的圆柱和这个长方形又有什么联系？
圆柱的高等于长方形的宽，圆柱的底面半径等于长方形的长。
4.教材第30页练习五第15题。 下面四个图形的面积都是36dm²。用这些图形分别卷成圆柱，哪个圆柱的体积最小？哪个圆柱的体积最大？你有什么发现？（单位：dm）
4.教材第30页练习五第15题。
如果把第一个长方形卷成圆柱,那么得到的圆柱和这个长方形有什么联系？
圆柱的底面周长就是长方形的长。圆柱的高就是长方形的宽。
4.教材第30页练习五第15题。 分别计算这四个长方形卷成圆柱之后的体积。（单位：dm）
这节课我们学习了什么？
1.一个圆柱形水桶，从里面量，底面直径是20cm,高是25cm。这个水桶的容积是多少立方分米？（得数保留一位小数） 2.如图，横截面直径为2dm的一根圆木，截成两段后，两段的表面积之和为75.36dm²。求原来那根圆木的体积。