人教版八年级下册18.2.1 矩形教学ppt课件

这是一份人教版八年级下册18.2.1 矩形教学ppt课件，共30页。PPT课件主要包含了学习目标，生活中的实例，比一比知关系，作业练习等内容，欢迎下载使用。
1.理解矩形的意义，知道矩形与平行四边形的区别与联系. 2.掌握矩形的性质及其推论，会进行有关的计算与证明.
重点：矩形的性质及其推论. 难点：矩形性质的运用.
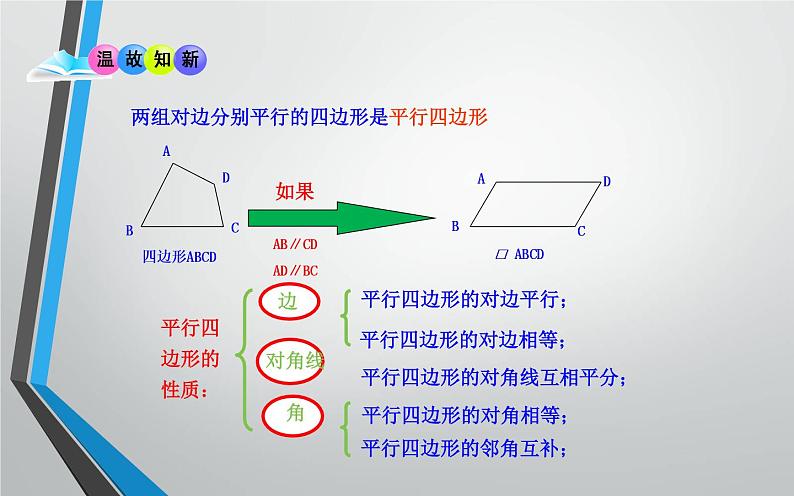
两组对边分别平行的四边形是平行四边形
平行四边形的对边平行；
平行四边形的对边相等；
平行四边形的对角相等；
平行四边形的邻角互补；
平行四边形的对角线互相平分；
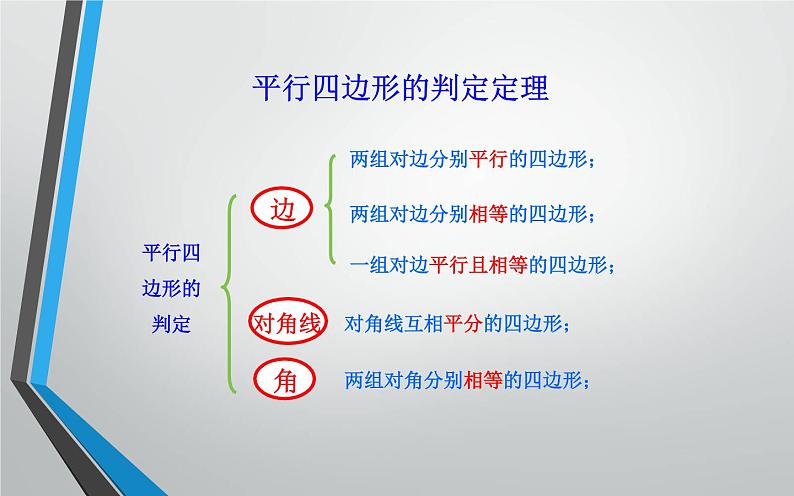
两组对边分别平行的四边形；
两组对边分别相等的四边形；
两组对角分别相等的四边形；
对角线互相平分的四边形；
一组对边平行且相等的四边形；
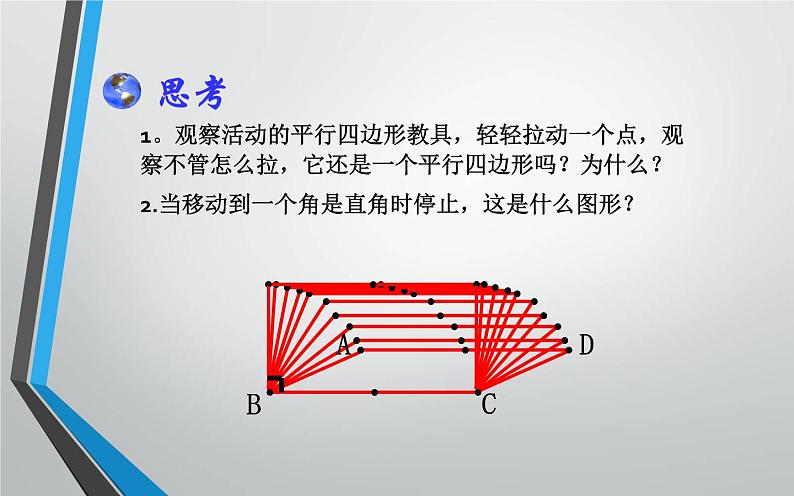
1。观察活动的平行四边形教具，轻轻拉动一个点，观察不管怎么拉，它还是一个平行四边形吗？为什么？2.当移动到一个角是直角时停止，这是什么图形？
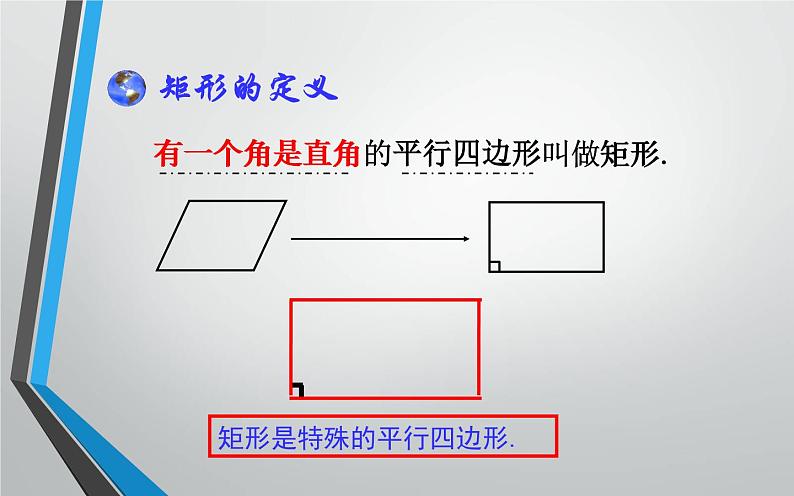
有一个角是直角的平行四边形
矩形是特殊的平行四边形.
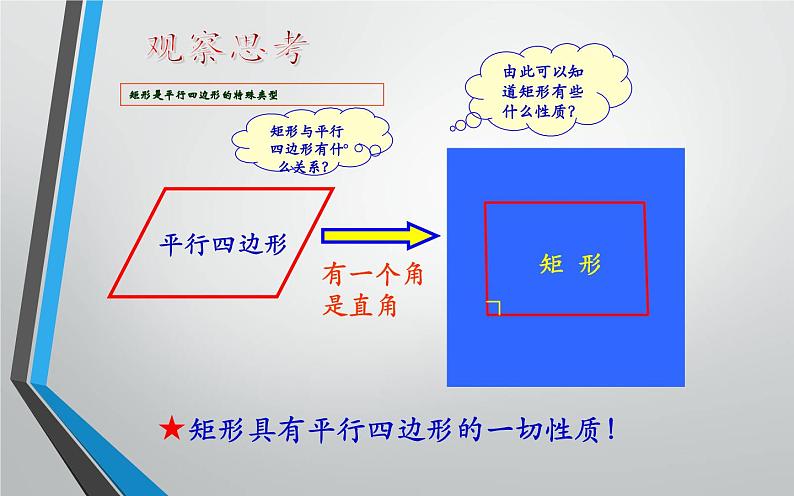
★矩形具有平行四边形的一切性质！
矩形是平行四边形的特殊类型
矩形与平行四边形有什么关系？
由此可以知道矩形有些什么性质？
矩形是一个特殊的平行四边形，除了具有平行四边形的所有性质外，还有哪些特殊性质呢？
如图，当□ABCD的一个角变为直角，我们知道，此时，四边形变为一个矩形。其它三个角又将会是什么样的角呢？
矩形的四个角都是直角。
已知：如图，四边形ABCD是矩形
求证：∠A=∠B=∠C=∠D=90°
证明：∵四边形ABCD是矩形
又∵矩形ABCD是平行四边形
∴ ∠A=∠C ∠B = ∠D∠A +∠B = 180°
∴ ∠A=∠B=∠C=∠D=90°即矩形的四个角都是直角
矩形的四个角都相等，都是900。
如图，当□ABCD的一个角变为直角，我们知道，此时，四边形变为一个矩形。它的两条对角线有什么关系？
矩形的两条对角线相等。
已知：如图，矩形ABCD的对角线AC、BD相交于点O。求证：AC=BD。
证明：在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC ， BC = CB
∴AC = BD 即矩形的对角线相等
矩形的两条对角线相等且互相平分，变形为直角三角形，你有什么发现？
直角三角形斜边上的中线等于斜边的一半。
∵∠ABC=90 ° ∴□ABCD是矩形
证明: 延长BO至D,使OD=BO, 连结AD、DC.
∵AO=OC, BO=OD∴四边形ABCD是平行四边形.
∴BO= BD= AC
1.矩形具有而一般平行四边形不一定具有的性质是（ ）
A.对边相等B.对角相等 C.对角互补D.对角线互相平分
2.直角三角形中，两直角边长分别为12和5，则斜边的中线长是（ ）
A.26 B.13C.8.5 D.6.5
矩形的 两条对角线互相平分
矩形的两组对边分别相等
矩形的两组对边分别平行
矩形 的两条对角线相等
∵四边形ABCD是矩形
∴AD = BC ，CD = AB
∴AD ∥BC ，CD ∥AB
∴AO= CO ，OD = OB
例1: 如图，矩形ABCD的两条对角线相交于点O，∠AOB=60°,AB=4㎝,求矩形对角线的长.
∴AC与BD相等且互相平分
∴ △AOB是等边三角形
∴ OA=AB=4㎝
∴ 矩形的对角线长 AC=BD=2OA=8㎝
解：∵ 四边形ABCD是矩形
P53练习2：已知：如图，矩形ABCD的两条对角线相交于点O，∠AOD=120°，AC=8cm，求矩形的边长.
∵ ∠AOD=120°
∴ △AOB为等边三角形
∴AB=OA= =4cm
方法小结: 如果矩形两对角线的夹角是60°或120°, 则其中必有一对等边三角形和有一个锐角是30°的直角三角形
1.如图，在矩形ABCD中，对角线AC、BD相交于点O，若OA=2，则BD的长为( )A.4 B .3 C .2 D.1
2.已知矩形的一条对角线与一边的夹角是40°，则两条对角线所成锐角的度数为( )A.50 ° B.60 ° C.70°D.80°
3.直角三角形中，两直角边分别是12和5，则斜边上的中线长是( )A.34 B.26 C.8.5 D.6.5
4、下面性质中，矩形不一定具有的是（ ）A．对角线相等 B．四个角都相等 C．是轴对称图形 D．对角线垂直
5. 矩形ABCD中，AB=2BC，E在CD上，AE=AB，则∠BAE等于（ ）A．30° B．45° C．60° D．120°
6.已知△ABC是直角三角形，∠ABC=90°，BD是斜边AC上的中线
(1)若BD=3㎝，则AC＝ _______ ㎝(2)若∠C=30°，AB＝5㎝，则AC＝_______㎝， BD＝_______㎝.
1、预习下一节内容:矩形的判定2、完成作业练习
3.如图，在矩形ABCD中，AC与BD交于O点，BE⊥AC于E，CF⊥BD于F，求证：BE=CF.
证明：∵AC、BD为矩形ABCD的对角线，∴OB=OC.又∵∠BEO=∠CFO=90°，∠EOB=∠FOC.∴Rt△EBO≌Rt△FCO,∴BE=CF.
4.如图，在Rt△ABC中，∠A=30°，∠ACB=90°. 点D是AB边的中点. 试判断△BCD的形状，并说明理由.
在Rt△ABC中，∠A=30°，∴∠B=90°-∠A=60°.在△CBD中，CD=BD，∠B=60°，∴△BCD为等边三角形.