人教版八年级下册17.1 勾股定理教学ppt课件

这是一份人教版八年级下册17.1 勾股定理教学ppt课件，共34页。PPT课件主要包含了第一章你还记得吗，互逆命题，关卡1分类讨论思想，分类讨论思想，关卡2方程思想，X+1米，方程思想，关卡3展开思想，周长的一半，展开思想等内容，欢迎下载使用。

形 数
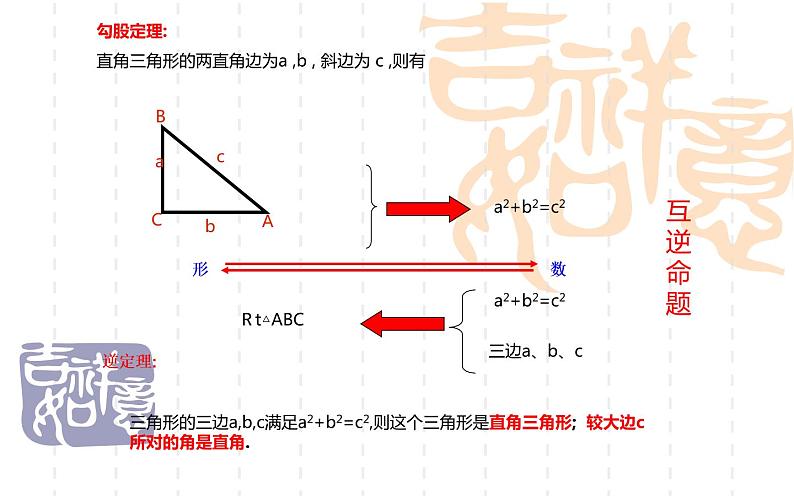
勾股定理:直角三角形的两直角边为a ,b , 斜边为 c ,则有
三角形的三边a,b,c满足a2+b2=c2,则这个三角形是直角三角形; 较大边c 所对的角是直角.
第二章：我们一起练习吧！
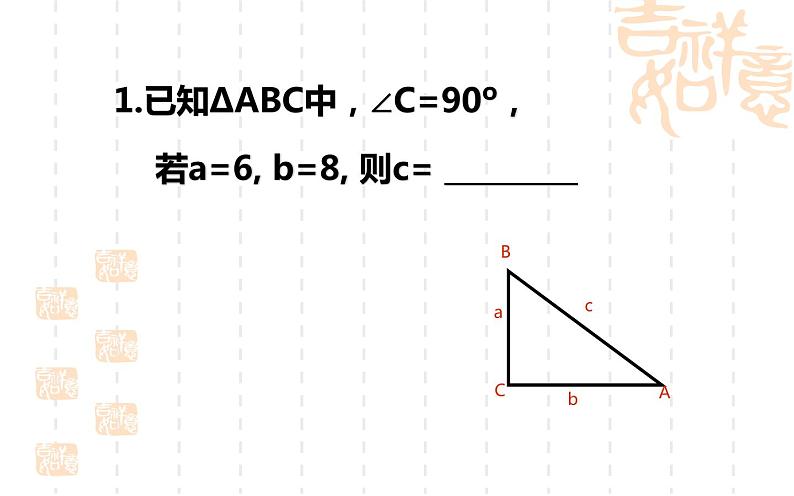
若a=6, b=8, 则c= _________
1.已知ΔABC中，∠C=90º，
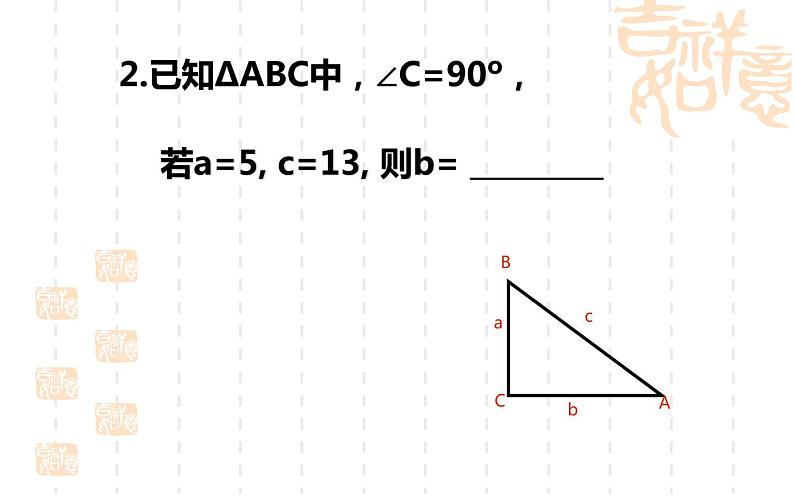
若a=5, c=13, 则b= _________
2.已知ΔABC中，∠C=90º，
3.判断：下面以a、b、c 为边的三角形是不是直角三角形？
　a=0.5，b=1.3，c=1.2
4.判断：下面以a、b、c 为边的三角形 是不是直角三角形？
　a=2，b=3，c=4
5.下列不是一组勾股数的是（ ）A、5、12、13 B、 C、12、16、20 D、 7、24、25
勾股数的妙用:你能速算吗?
3.已知直角三角形中,∠c=90°，(1)a=3,b=4,c=_____(2)a=9,b=____c=15(3)a=____,b=40,c=50(4)a=24,b=32,c=________(5)a=5,b=_______,c=13(6)a=_____,b=36,c=39(7)a=25,b=60,c=________
你计算的很快呀，怎么做的?跟我们分享一下吧！
6.已知数7和24，请你再写一个整数，使得这个数正好是一个直角三角形第三边的长，这个数可以是 ___________.
7.一个直角三角形的三边长是不大于10的三个连续的偶数，则它的周长是 __________.
第三章：我们一起闯关吧吧！
2.三角形ABC中,AB=10,AC=17,BC边上的高线 AD=8,求BC的长。
1.直角三角形中，已知两边的长、另一边不知道时，应分类讨论。
2.当已知条件中没有给出图形时，应认真读句画图，避免遗漏另一种情况。
分类讨论思想，在直角三角形中的规律总结。
１、小强想知道学校旗杆的高，他发现旗杆顶端的绳子垂到地面还多1米，当他把绳子的下端拉开5米后，发现下端刚好接触地面，你能帮他算出来吗？
2、折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8CM,BC=10CM,求CF和EC的长.
1.小明家住在18层的高楼，一天，他与妈妈去买竹竿。
快点回家，好用它凉衣服。
糟糕，太长了，放不进去。
如果电梯的长、宽、高分别是3米、4米、12米，那么，能放入电梯内的竹竿的最大长度是多少米？
2.如图是一个三级台阶，它的每一级的长宽和高分别为20dm、3dm、2dm，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿着台阶面爬到B点最短路程是多少？
3.如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程( 取3）是( ) A.20cm B.10cm C.14cm D.无法确定
1. 几何体的表面路径最短的问题，一般展开表面成平面。
2.利用两点之间线段最短，及勾股定理求解。
1.小区里有一块四边形的绿化带，其中∠B＝900，AB＝3，BC＝4，CD＝12，AD＝13, 你能求出绿化带的面积吗?
2.小区里有一块四边形的绿化带，∠B＝900，AB＝3，BC＝4，CD＝12，AD＝13,你能求出绿化带的面积吗?
3.如图，在三角形ABC中，AB=AC,D在BC的延长线上，求证：AD²-AB²=BD·CD