






初中数学第十七章 勾股定理综合与测试教学ppt课件
展开(3)分清直角边、斜边
勾股定理及其数学语言表达式:
直角三角形两直角边a、b的平方和等于斜边c的平方。
(1)公式变形 等
吴建闯想知道我校旗杆的高度。
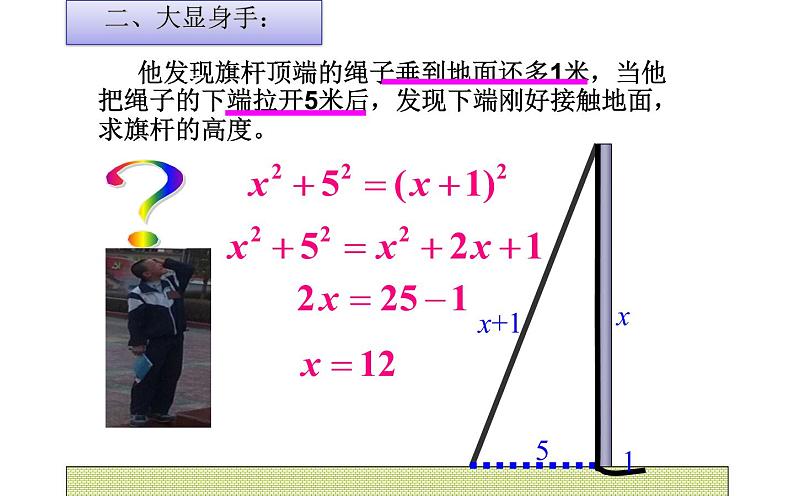
他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,求旗杆的高度。
直角三角形中,当无法已知两边求第三边时,应采用间接求法:灵活地寻找题中的等量关系,利用勾股定理列方程(方程思想)。
问题:上述题给你的启发是什么?
例1、如图,一块直角三角形的纸片,两直角边AC=6㎝,BC=8㎝。现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长.
问题:应用勾股定理解决折叠问题解题步骤是怎样的?
已知,在△ABC中,∠C=900,AC= cm,BC=3cm,将△ABC折叠,使点B与点A重合,折痕为DE。CD = cm.
例2:如图所示,将长方形纸片ABCD的一边AD向下折叠,点D落在BC边的F处。已知AB=CD=8cm,BC=AD=10cm,求EC的长。
长方形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,折痕是EF,DE= cm
1.如图,已知直角三角形ABC中, ∠C=90°,若AC=4,AB=5,则BC = ____.
2.如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则AE的长为____.
3.如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为____.
课本28页第5题课本38页第3、10题
1、如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,将△BCD沿BD折叠,使点C落在边AB上的点C′处,则折痕BD的长为________.
2:若直角三角形的三边长分别为2、 4、 x,则x= ____.
中考数学复习微专题(二)矩形的折叠问题教学课件: 这是一份中考数学复习微专题(二)矩形的折叠问题教学课件,共11页。
中考数学复习微专题(六)矩形的折叠问题教学课件: 这是一份中考数学复习微专题(六)矩形的折叠问题教学课件,共11页。
人教版八年级下册17.1 勾股定理教学课件ppt: 这是一份人教版八年级下册17.1 勾股定理教学课件ppt,共18页。PPT课件主要包含了动手折一折,温故互查,自主尝试与合作探究,拓展练习,本节课的收获等内容,欢迎下载使用。













