初中数学人教版八年级上册13.1.1 轴对称同步测试题
展开人教版 八年级上册数学 13.1 轴对称 针对训练
一、选择题
1. 如图所示,线段AB,AC的垂直平分线相交于点P,则PB与PC的关系是( )
A.PB>PC B.PB=PC
C.PB<PC D.PB=2PC
2. 如图,在△ABC中,∠ACB=90°,∠B=22.5°,AB边的垂直平分线交BC于点D,则下列结论中错误的是( )
A.∠ADC=45° B.∠DAC=45°
C.BD=AD D.BD=DC
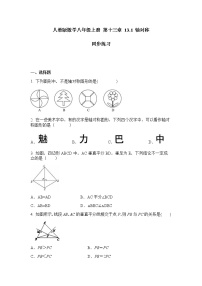
3. 在汉字“生活中的日常用品”中,是轴对称图形的有 ( )
A.2个 B.3个 C.4个 D.5个
4. 如图,在△ABC中,DE垂直平分AB,交AB于点E,交BC于点D,若AD=4,BC=3DC,则BC等于 ( )
A.4 B.4.5 C.5 D.6
5. 在数学课上,老师提出如下问题:如图,已知△ABC中,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PB=BC.下面是四名同学的作法,其中正确的是 ( )
6. 将平面直角坐标系内某个图形的各个点的横坐标都乘-1,纵坐标不变,则所得图形与原图形的关系是( )
A.关于x轴对称 B.关于y轴对称
C.图形向左平移 D.图形向下平移
7. 如图,△ABC中,点D在BC上,∠B=62°,∠C=53°,将点D分别以AB,AC所在直线为对称轴,画出对称点E,F,并连接AE,AF,则∠EAF的度数为 ( )
A.124° B.115° C.130° D.106°
8. 如图,在△ABC中,点D在BC上,将点D分别以AB,AC为对称轴,画出对称点E,F,并连接AE,AF.根据图中标示的角度,∠EAF的度数为( )
A.113° B.124°
C.129° D.134°
9. 如图,在中,,分别以点和点为圆心,大于的长为半径作弧,两弧相交于两点,作直线交于点,交于点,连接.若,,则的长为
A. B.
C. D.
10. 如图,C,E是直线l两侧的点,以点C为圆心,CE的长为半径画弧交直线l于A,B两点.又分别以点A,B为圆心,大于AB的长为半径画弧,两弧交于点D,连接CA,CB,CD,则下列结论不一定正确的是 ( )
A.CD⊥直线l
B.点A,B关于直线CD对称
C.点C,D关于直线l对称
D.CD平分∠ACB
二、填空题
11. 如图所示的4组图形中,左右两个图形成轴对称的是第________组(填序号).
12. 如图,△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为________.
13. 如图所示图案是几种车的标志,在这几个图案中,轴对称图形有________个,其中只有一条对称轴的轴对称图形有________个,对称轴最多的轴对称图形有________条对称轴.
14. 如图,DE是△ABC的边AC的垂直平分线,若BC=9,AD=4,则BD=________.
15. 现要在三角地带ABC内(如图)建一座中心医院,使医院到A,B两个居民小区的距离相等,并且到公路AB和AC的距离也相等,请你确定这座中心医院的位置.
三、作图题
16. 小强拿几张正方形的纸(如图4①),沿虚线对折一次得到图②,再沿虚线对折一次得到图③,然后用剪刀沿图④中不同位置的虚线剪去中心的一块,请参照例图,在后面的正方形中画出图④的纸片打开后的形状.(不写作法,保留作图痕迹)
17. 如图,已知△ABC.
(1)用直尺和圆规分别作出AB,AC边的垂直平分线l1,l2;
(2)若直线l1,l2的交点为O,连接OB,OC.求证:OB=OC.
四、解答题
18. 图中的两个图形关于某条直线对称,根据图中提供的条件求出x,y的值.
19. 如图所示,两个四边形关于直线l对称,∠C=90°,试写出边a,b的长,并求出∠G的度数.
20. 如图,在△ABE中,AD⊥BE于点D,C是BE上一点,DC=BD,且点C在AE的垂直平分线上.若△ABC的周长为22 cm,求DE的长.
21. 如图,Rt△ABC的顶点A,B,C关于直线MN的对称点分别为A',B',C',其中
∠A=90°,AC=8 cm,点C,B,A'在同一条直线上,且A'C=12 cm.
(1)求△A'B'C'的周长;
(2)求△A'CC'的面积.
22. 已知:如图,∠BAC的平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:BE=CF;
(2)若AF=6,BC=7,求△ABC的周长.
人教版 八年级上册数学 13.1 轴对称 针对训练 -答案
一、选择题
1. 【答案】B [解析] 如图,连接AP.
∵线段AB,AC的垂直平分线相交于点P,∴AP=PB,AP=PC.∴PB=PC.
2. 【答案】D [解析] ∵AB的垂直平分线交BC于点D,∴AD=BD,故C正确;∵AD=BD,∴∠B=∠BAD=22.5°.∴∠ADC=45°,故A正确;∠DAC=90°-∠ADC=90°-45°=45°,故B正确.故选D.
3. 【答案】B [解析] 根据轴对称图形的定义,在汉字“生活中的日常用品”中,是轴对称图形的有“中”“日”“品”3个.故选B.
4. 【答案】D [解析] ∵DE垂直平分AB,AD=4,
∴BD=AD=4.
∵BC=3DC,
∴BD=2CD.
∴CD=2.
∴BC=BD+CD=6.故选D.
5. 【答案】C [解析] ∵PA+PB=BC,而PC+PB=BC,∴PA=PC.∴点P为线段AC的垂直平分线与BC的交点.显然只有选项C符合题意.
6. 【答案】B [解析] 点的横坐标乘-1后变为原来的相反数,又因为纵坐标不变,故变化后的点与原来的点关于y轴对称.
7. 【答案】C [解析] 连接AD,如图.
∵点D分别以AB,AC所在直线为对称轴,画出对称点E,F,
∴∠EAB=∠BAD,∠FAC=∠CAD.
∵∠B=62°,∠C=53°,∴∠BAC=∠BAD+∠DAC=180°-62°-53°=65°.
∴∠EAF=2∠BAC=130°.
故选C.
8. 【答案】D [解析] 连接AD.
∵点D分别以AB,AC为对称轴,画出对称点E,F,∴∠EAB=∠BAD,∠FAC=∠CAD.
∵∠B=62°,∠C=51°,
∴∠BAC=∠BAD+∠CAD=67°.
∴∠EAF=2∠BAC=134°.
9. 【答案】A
【解析】由作法得垂直平分,
∴,,,
∵,∴,∴,
∴为斜边上的中线,
∵,
∴.故选A.
10. 【答案】C [解析] 由作法可知CD垂直平分AB,
故选项A,B正确;
∵CD垂直平分AB,∴CA=CB.
设CD与AB交于点G,
易证Rt△ACG≌Rt△BCG,∴∠ACG=∠BCG,
即CD平分∠ACB,故选项D正确;
∵AB不一定平分CD,故选项C错误.
故选C.
二、填空题
11. 【答案】(3)(4)
12. 【答案】13 【解析】∵DE垂直平分AB,∴AE=BE,∵AE+EC=8,∴EC+BE=8,∴△BCE的周长为BE+EC+BC=13.
13. 【答案】3 2 2
14. 【答案】5
15. 【答案】解:作线段AB的垂直平分线EF,作∠BAC的平分线AM,EF与AM相交于点P,则点P处即为这座中心医院的位置.
三、作图题
16. 【答案】
解:如图所示:
17. 【答案】
解:(1)如图所示.
(2)证明:如图,连接OA.
∵l1是AB的垂直平分线,
∴OA=OB.
同理,OA=OC.
∴OB=OC.
四、解答题
18. 【答案】
[解析] 因为两个图形关于某条直线对称,所以观察发现A和F,B和E,C和H,D和G分别是对称点,因此CD边与HG边是对应边,长度相等,∠ADC和∠FGH是对应角,大小相等.
解:x=∠ADC=360°-40°-95°-110°=115°,y=HG=3.
19. 【答案】
解:∵两个四边形关于直线l对称,
∴四边形ABCD≌四边形FEHG,
∴∠H=∠C=90°,∠A=∠F=80°,∠E=∠B=135°,a=5 cm,b=4 cm.
∴∠G=360°-∠H-∠E-∠F=55°.
20. 【答案】
解:∵BD=DC,AD⊥BE,∴AB=AC.
∵点C在AE的垂直平分线上,∴AC=CE.
∵△ABC的周长是22 cm,
∴AC+AB+BD+CD=22 cm.
∴AC+CD=11 cm.
∴DE=CD+CE=CD+AC=11 cm.
21. 【答案】
解:(1)∵Rt△ABC的顶点A,B,C关于直线MN的对称点分别为A',B',C',AC=8 cm,A'C=8cm,
∴AB=A'B',AC=A'C',∠A'=∠A=90°.
∴△A'B'C'的周长为A'C'+B'C'+A'B'=AC+A'C=12+8=20(cm).
(2)由(1)得A'C'=AC=8 cm,∠A'=90°,
∴△A'CC'的面积为A'C·A'C'=×12×8=48(cm2).
22. 【答案】
(1)证明:如图,连接CD.
∵点D在BC的垂直平分线上,∴BD=CD.
∵DE⊥AB,DF⊥AC,AD平分∠BAC,
∴DE=DF,∠BED=∠CFD=90°.
在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL).∴BE=CF.
(2)在Rt△ADE和Rt△ADF中,
∴Rt△ADE≌Rt△ADF.
∴AE=AF=6.
∴△ABC的周长=AB+BC+AC=(AE+BE)+BC+(AF-CF)=6+7+6=19.
人教版八年级上册第十三章 轴对称13.1 轴对称13.1.1 轴对称同步训练题: 这是一份人教版八年级上册第十三章 轴对称13.1 轴对称13.1.1 轴对称同步训练题,共6页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
初中人教版13.1.1 轴对称当堂检测题: 这是一份初中人教版13.1.1 轴对称当堂检测题,共6页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
初中数学人教版八年级上册13.1.1 轴对称当堂达标检测题: 这是一份初中数学人教版八年级上册13.1.1 轴对称当堂达标检测题,共7页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。