人教版新课标A选修2-1第一章 常用逻辑用语1.1命题及其关系示范课课件ppt

这是一份人教版新课标A选修2-1第一章 常用逻辑用语1.1命题及其关系示范课课件ppt，共39页。PPT课件主要包含了逆否命题，互逆命题，互否命题，它们之间的关系为，条件分析，失分警示等内容，欢迎下载使用。

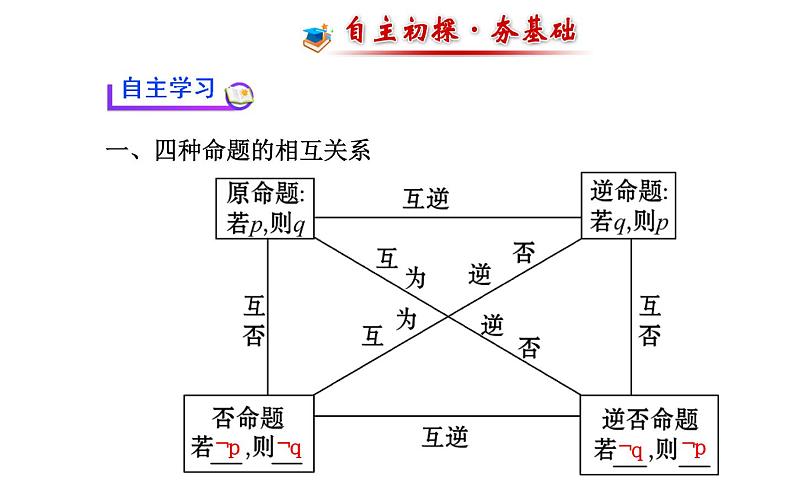
一、四种命题的相互关系
思考:在四种命题中,具有互逆、互否、互为逆否关系的命题各有两对?提示:正确,从四种命题的相互关系图中可以看出这几种关系各有两对.
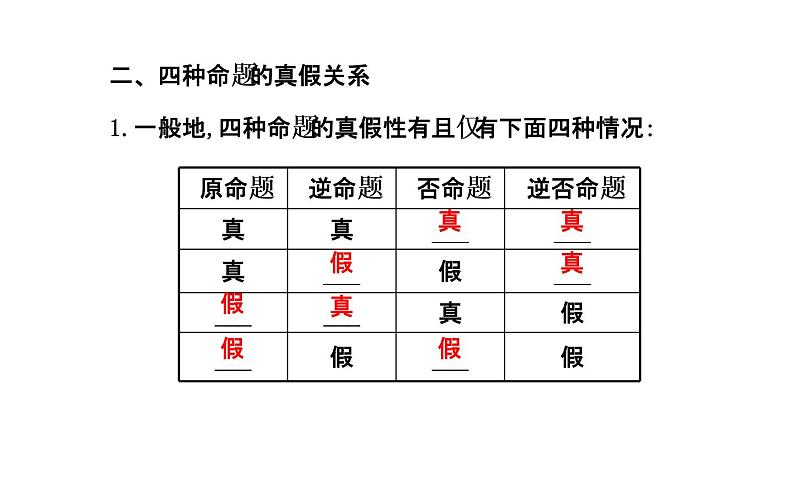
二、四种命题的真假关系1.一般地,四种命题的真假性有且仅有下面四种情况:
2.四种命题的真假性之间的关系:(1)两个命题互为_________,它们有相同的真假性.(2)两个命题为_________或_________,其真假性没有关系.判断:(正确的打“√”,错误的打“×”)(1)两个互逆命题的真假性相同.(　　)(2)原命题的逆命题与原命题的否命题真假性相同.(　　)(3)对于一个命题的四种命题,可以一个真命题也没有.(　　)
提示:(1)错误.两个互逆命题的真假性没有关系,可能一个真命题也没有.(2)正确.原命题的逆命题与原命题的否命题互为逆否命题,真假性相同,为等价命题.(3)正确.一个命题的四种命题中,可能都是假命题,如若01,此命题的四种命题均为假命题.答案:(1)×　(2)√　(3)√
【知识点拨】1.对四种命题相互关系的两点认识(1)四种命题中,任意确定一个为原命题,其逆命题、否命题、逆否命题就确定了,所以“互逆”“互否”“互为逆否”具有对称特征.(2)在原命题、逆命题、否命题与逆否命题这四种命题中,记原命题为a、逆命题为b、否命题为c、逆否命题为d,四种命题中共有6对命题:a与b,a与c,a与d,b与c,b与d,c与d.
2.对四种命题真假关系的两点说明(1)由于一个命题与其逆否命题具有相同的真假性,四种命题中有两对互为逆否命题,所以四种命题中真命题的个数必须是偶数,即真命题可能有4个、2个或0个.(2)由于原命题与其逆否命题的真假性相同,所以原命题与其逆否命题是等价命题,因此,当直接证明原命题困难时,可以转化为证明与其等价的逆否命题,这种证法是间接证明命题的方法,也是反证法的一种变通形式.
类型一 四种命题的相互关系 【典型例题】1.下列四个命题:①“若x+y=0,则x,y互为相反数”的否命题;②“若a>b,则a2>b2”的逆否命题;③“若x≤-3,则x2-x-6>0”的否命题;④“对顶角相等”的逆命题.其中真命题的个数是(　　)A.0　　　 B.1　　 　C.2　 　　D.3
2.判断命题“如果m>0,则x2+x-m=0有实数根”的逆否命题的真假.【解题探究】1.写四种命题的关键是什么?2.一个命题与它的逆否命题的真假性之间有什么关系?探究提示:1.写一个命题的逆命题、否命题和逆否命题关键是分清命题的条件和结论.2.一个命题与它的逆否命题同真同假.
【解析】1.选B.①否命题:若x+y≠0,则x,y不互为相反数,真命题.②逆否命题:若a2≤b2,则a≤b,假命题.③否命题:若x>-3,则x2-x-6≤0,假命题.④逆命题:相等的两个角是对顶角,假命题.故选B.
2.方法一:∵m>0,∴4m>0,∴4m+1>0,∴方程x2+x-m=0的判别式Δ=4m+1>0.∴方程x2+x-m=0有实数根.∴原命题“如果m>0,则x2+x-m=0有实数根”为真.又因原命题与它的逆否命题等价,所以“如果m>0,则x2+x-m=0有实数根”的逆否命题也为真.
方法二:原命题“如果m>0,则x2+x-m=0有实数根”的逆否命题为“如果x2+x-m=0无实数根,则m≤0”.∵x2+x-m=0无实数根,∴Δ=4m+1<0,∴m<- ≤0,∴命题“如果x2+x-m=0无实数根,则m≤0”为真.
【拓展提升】判断四种命题之间四种关系的两种方法方法一:利用四种命题的定义判断;方法二:可以巧用“逆、否”两字进行判断,如“逆命题”与“逆否命题”中不同有“否”字,是互否关系;而“逆命题”与“否命题”中不同有“逆、否”二字,其关系为逆否关系.
【变式训练】下列命题中为真命题的是(　　)A.命题“若x>y,则x>|y|”的逆命题B.命题“若x>1,则x2>1”的逆命题C.命题“若x=1,则x2+x-2=0”的否命题D.命题“若x2>0,则x>1”的逆否命题【解题指南】先写出相应命题再判断或根据其等价关系判断.
【解析】选A.因为选项A:逆命题为“x>|y|,所以x>0”.当y≥0时,x>y;当y<0时,x>-y>y,所以x>y.命题“若x>y,则x>|y|”的逆命题是真命题;选项B:逆命题为“若x2>1,则x>1”,是假命题.因为x2>1,所以x<-1或x>1;选项C:它的否命题是“若x≠1,则x2+x-2≠0”.因为x≠1时,x2+x-2可以为0,所以是假命题;选项D:因为原命题是假命题,所以它的逆否命题也是假命题.
类型 二 原命题与逆否命题的等价性应用 【典型例题】1.“正弦值不相等的两个角的终边不相同”是　　　　命题(填真、假).2.判断下列命题的真假,并说明理由:(1)若x2≠9,则x≠3.(2)若方程x2+2ax+a2+a-1=0无实数根,则a≤2.
【解题探究】1.题1中命题的条件与结论有什么特点?2.当直接判断一个命题的真假比较困难时,我们一般如何处理?探究提示:1.命题的条件和结论都是否定的形式.2.当直接判断命题的真假困难时,可以判断其逆否命题的真假.
【解析】1.“正弦值不相等的两个角的终边不相同”的逆否命题为“终边相同的两个角的正弦值相等”是真命题,所以原命题是真命题.答案:真
2.(1)原命题:若x2≠9,则x≠3;逆否命题:若x=3,则x2=9,是真命题,所以原命题是真命题.(2)原命题:若方程x2+2ax+a2+a-1=0无实数根,则a≤2;逆否命题:若a>2,则方程x2+2ax+a2+a-1=0有实数根.若a>2,则-a<-2,Δ=(2a)2-4(a2+a-1)=4(1-a)<0,所以方程x2+2ax+a2+a-1=0无实数根,逆否命题是假命题,所以原命题为假命题.
【互动探究】若题2(2)的命题变为:若a>1,则方程x2+2ax+a2+a-1=0无实数根,如何判断此命题的真假?【解析】命题“若a>1,则方程x2+2ax+a2+a-1=0无实数根”的逆否命题为“若方程x2+2ax+a2+a-1=0有实数根,则a≤1”,由于Δ=(2a)2-4(a2+a-1)=4(1-a)≥0,得a≤1,故原命题是真命题.
【拓展提升】原命题与逆否命题等价关系的应用(1)若一个命题的条件或结论含有否定词时,直接判断命题的真假较为困难,这时可以转化为判断它的逆否命题的真假.(2)当证明某一个命题有困难时,可以证明它的逆否命题为真(假)命题,来间接地证明原命题为真(假)命题.
【变式训练】判断下列命题的真假,并说明理由:(1)不内接于圆的四边形的对角不互补.(2)若a+b<0,则a,b至少有一个小于0.【解析】(1)“不内接于圆的四边形的对角不互补”的逆否命题为“对角互补的四边形内接于圆”,真命题,所以原命题是真命题.(2)“若a+b<0,则a,b至少有一个小于0”的逆否命题为“若a≥0,b≥0,则a+b≥0”,真命题,所以原命题是真命题.
【规范解答】等价命题在证明中的应用【典例】
【规范解答】证明原命题的逆否命题成立,原命题为“若p3+q3=2,则p+q≤2”,其逆否命题为“若p+q>2,则p3+q3≠2”.证明如下:……………………………………………………2分若p+q>2①,
则p>2-q,………………………………………………………3分∴p3 >(2-q)3②,………………………………………………4分∴p3+q3>(2-q)3+q3.…………………………………………6分又(2-q)3+q3=(8-12q+6q2-q3)+q3…………………………………………8分=6q2-12q+8=6(q-1)2+2≥2.③……………………………………………10分
∴p3+q3>2,即p3+q3≠2,…………………………………………………11分这表明原命题的逆否命题为真命题,从而原命题也为真命题. ………………………………………………………………12分
【防范措施】1.正难则反思想的应用若判断或证明一个命题有困难时,可以利用等价命题即它的逆否命题来处理,如本例直接证明有困难,可以证明它的逆否命题的真假来说明原命题的真假.2.不等式性质的应用不等式的性质在证明不等式的应用中具有重要的作用,解决问题时要灵活应用,如本例中由a>b可推出a3>b3(但由a>b不一定推出a2>b2).
【类题试解】若a2+b2=c2,求证:a,b,c不可能都是奇数.【证明】依题意,就是证明命题“若a2+b2=c2,则a,b,c不可能都是奇数”为真命题.为此,只需证明其逆否命题“若a,b,c都是奇数,则a2+b2≠c2”为真命题.∵a,b,c都是奇数,则a2,b2,c2都是奇数.于是a2+b2为偶数,而c2为奇数,即a2+b2≠c2.∴原命题的逆否命题为真命题,∴原命题成立.
1.与命题“若m∈M,则n∉M”等价的命题是(　　)A.若m∉M,则n∉M　　　　 B.若n∉M,则m∈MC.若m∉M,则n∈M D.若n∈M,则m∉M【解析】选D.与命题等价的命题是其逆否命题,故选D.
2.给出命题:若函数y=f(x)是幂函数,则它的图象不过第四象限,在它的逆命题、否命题、逆否命题三个命题中,真命题的个数是(　　)A.3　　　 　 B.2　　 　　C.1　　　 　D.0
【解析】选C.逆命题:若函数y=f(x)图象不过第四象限,则这个函数是幂函数,假命题.否命题:若函数y=f(x)不是幂函数,则它的图象过第四象限,假命题.逆否命题:若函数y=f(x)的图象过第四象限,则它不是幂函数,真命题.
3.“若tanθ= ,则θ=60°”的否命题是　　　　　,否命题是　　　　命题(填真、假).【解析】“若tanθ= ,则θ=60°”的否命题是“若tanθ≠ ,则θ≠60°”,是真命题.答案:若tanθ≠ ,则θ≠60°　真
4.命题“常用对数不是1的数不是10”的逆否命题为　　　　　　,是　　　　命题(填真、假).【解析】命题“常用对数不是1的数不是10”的逆否命题为“10的常用对数是1”,是真命题.答案:10的常用对数是1　真
5.写出命题“设x为实数,若x>0,则x2>0”的逆命题、否命题、逆否命题,并判断它们的真假.【解析】逆命题:设x为实数,若x2>0,则x>0,逆命题为假命题;否命题:设x为实数,若x≤0,则x2≤0,否命题为假命题;逆否命题:设x为实数,若x2≤0,则x≤0,逆否命题为真命题.