人教版新课标A选修2-12.4抛物线说课ppt课件

这是一份人教版新课标A选修2-12.4抛物线说课ppt课件，共23页。PPT课件主要包含了抛物线的定义，MFd等内容，欢迎下载使用。

生活中存在着各种形式的抛物线
1.掌握抛物线的定义及标准方程.（重点）2.能求简单抛物线的方程.（重点、难点）
我们知道,二次函数y=ax2+bx+c(a≠0)的图象是一条抛物线，而且研究过它的顶点坐标、对称轴等问题.那么，抛物线到底有怎样的几何性质？它还有哪些几何性质？
探究点1 抛物线的定义
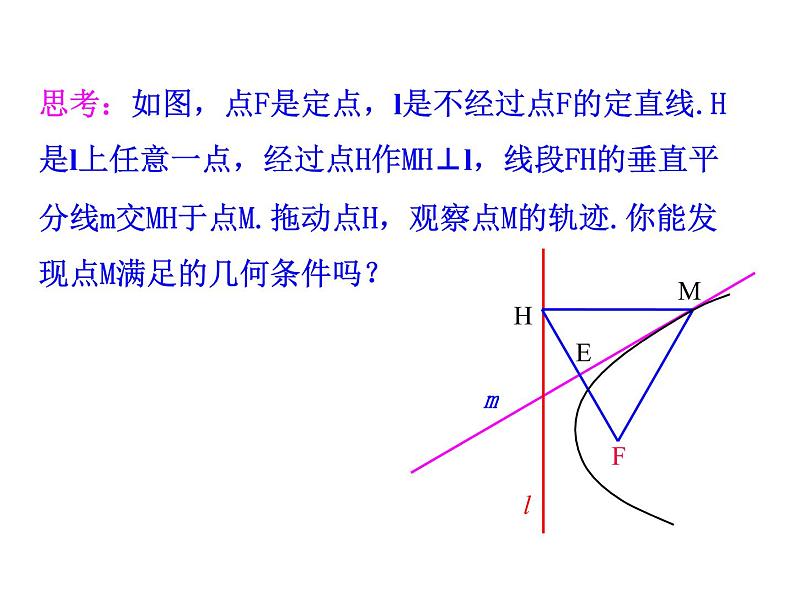
思考：如图，点F是定点，l是不经过点F的定直线.H是l上任意一点，经过点H作MH⊥l，线段FH的垂直平分线m交MH于点M.拖动点H，观察点M的轨迹.你能发现点M满足的几何条件吗？
一条经过点F且垂直于l 的直线
在平面内,与一个定点F和一条定直线l(l不经过点F) 距离相等的点的轨迹叫做抛物线.
点F叫做抛物线的焦点,直线l 叫做抛物线的准线.
想一想：定义中当直线l 经过定点F，则点M的轨迹是什么?
以过点F且垂直于直线 l 的直线为x轴,垂足为K.以FK的中点O为坐标原点建立直角坐标系xOy.
设M（x，y）是抛物线上任意一点，
由抛物线的定义，抛物线就是点的集合
探究点2 抛物线的标准方程
其中p为正常数，它的几何意义是:
方程 y2 = 2px（p＞0）表示焦点在x轴正半轴上的抛物线．
若抛物线的开口分别朝左、朝上、朝下，你能根据上述办法求出它的标准方程吗？
抛物线的标准方程还有哪些不同形式?
图 形
四种抛物线及其它们的标准方程
y2=2px(p>0)
y2=-2px (p>0)
x2=2py (p>0)
x2=-2py (p>0)
（1）若一次项的变量为X（或Y），则焦点就在X轴（或Y轴）上；
如何判断抛物线的焦点位置，开口方向？
（2）一次项的系数的正负决定了开口方向
即：焦点与一次项变量有关；正负决定开口方向！
【例1】(1)已知抛物线的标准方程是y2=6x,求它的焦点坐标和准线方程． (2)已知抛物线的焦点是F(0,-2)，求它的标准方程.
解:(1)因为ｐ＝３，故抛物线的焦点坐标为 ，准线方程为
(2)因为抛物线的焦点在y轴的负半轴上,且　　　　　　　故所求抛物线的标准方程为x2=-8y.
1.根据下列条件写出抛物线的标准方程.(1)焦点是（0，-3）；(2)准线是 .2.求下列抛物线的焦点坐标与准线方程.(1)y=8x2；(2)x2+8y=0.
【提升总结】(1)用待定系数法求抛物线标准方程,应先确定抛物线的形式，再求p值.(2)求抛物线的焦点坐标和准线方程要先化成抛物线的标准方程.
【例2】一种卫星接收天线的轴截面如图(1)所示.卫星波束呈近似平行状态射入轴截面为抛物线的接收天线，经反射聚集到焦点处.已知接收天线的口径(直径)为4.8m,深度为0.5m，试建立适当的坐标系，求抛物线的标准方程和焦点坐标.
解：如图(2)，在接收天线的轴截面所在平面内建立直角坐标系，使接收天线的顶点（即抛物线的顶点）与原点重合.
所以，所求抛物线的标准方程是 ,焦点坐标是（2.88，0）.
由已知条件可得，点A的坐标是（0.5，2.4），代入方程得
2．设抛物线y2＝8x上一点P到y轴的距离是4，则点P到该抛物线焦点的距离是（ ）A.12 B.4 C.6 D.8
3．已知动圆M 经过点A(3，0)，且与直线l：x＝－3相切，求动圆圆心M的轨迹方程．
解析：设动点M(x，y)，设圆M与直线l：x＝－3的切点为N，则|MA|＝|MN|，即动点M到定点A和定直线l：x＝－3的距离相等，所以点M的轨迹是抛物线，且以A(3，0)为焦点，以直线l：x＝－3为准线，所以 ＝3，所以p＝6.所以圆心M的轨迹方程是y2＝12x.
平面内与一个定点F的距离和一条定直线l (l不经过点F)的距离相等的点的轨迹叫做抛物线.
1.求抛物线标准方程；2.已知方程求焦点坐标和准线方程.
1.定义的前提条件：直线l不经过点F;2.p的几何意义：焦点到准线的距离；3.标准方程表示的是顶点在原点，对称轴为坐标轴的抛物线.
抛物线的标准方程有四种： y2=2px(p>0),y2=-2px(p>0)，x2=2py(p>0),x2=-2py(p>0).