






高中人教版新课标A1.不等式的基本性质背景图课件ppt
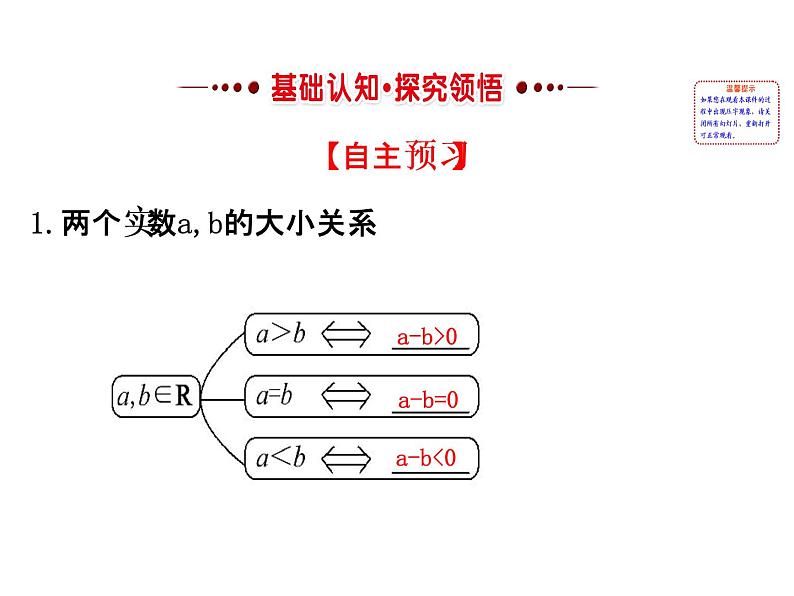
展开【自主预习】1.两个实数a,b的大小关系
2.不等式的基本性质(1)对称性:a>b⇔____.(2)传递性:a>b,b>c⇒____.(3)可加性:____⇔a+c>b+c.
(4)可乘性:如果a>b,c>0,那么______;如果a>b,c<0,那么______.(5)乘方:如果a>b>0,那么an__bn(n∈N,n≥2).(6)开方:如果a>b>0,那么 __ (n∈N,n≥2).
【即时小测】1.若a
【解析】选C.因为x2+3-2x=(x-1)2+2>0,所以(1)正确;a5+b5-(a3b2+a2b3)=(a2-b2)(a3-b3)=(a-b)2(a+b)(a2-ab+b2)正负不确定,所以(2)不正确;a2+b2-2(a-b-1)=(a-1)2+(b+1)2≥0.所以(3)正确.
【知识探究】 探究点 不等式的基本性质1.若a>b,c>d,那么a-c>b-d吗?提示:不一定成立,同向不等式具有可加性,但不具有可减性.如2>1,5>1,但2-5>1-1不成立.
2.若a>b,c>d,一定有ac>bd吗?提示:不一定,如a=-1,b=-2,c=-2,d=-3时就不成立.
【归纳总结】1.符号“⇒”和“⇔”的含义“⇒”与“⇔”,即推出关系和等价关系,或者说“不可逆关系”与“可逆关系”,这要求必须熟记和区别不同性质的条件.
2.性质(3)的作用它是移项的依据.不等式中任何一项改变符号后,可以把它从一边移到另一边.即a+b>c⇒a>c-b.性质(3)是可逆的,即a>b⇔a+c>b+c.
3.不等式的单向性和双向性性质(1)和(3)是双向的,其余的在一般情况下是不可逆的.
4.注意不等式成立的前提条件不可强化或弱化成立的条件.要克服“想当然”“显然成立”的思维定式.如传递性是有条件的;可乘性中c的正负,乘方、开方性质中的“正数”及“n∈N,且n≥2”都需要注意.
类型一 作差法比较大小【典例】设m≠n,x=m4-m3n,y=n3m-n4,比较x与y的大小.【解题探究】比较两个多项式的大小常用的方法是什么?提示:常用作差比较法.
【解析】因为x-y=(m4-m3n)-(mn3-n4)=(m-n)m3-n3(m-n)=(m-n)(m3-n3)=(m-n)2(m2+mn+n2)
又m≠n,所以(m-n)2>0,因为 所以x-y>0,故x>y.
【方法技巧】作差比较法的四个步骤
【变式训练】1.若f(x)=3x2-x+1,g(x)=2x2+x-1,则f(x)与g(x)的大小关系是_________.
【解析】f(x)-g(x)=3x2-x+1-(2x2+x-1)=x2-2x+2=(x-1)2+1≥1>0,所以f(x)>g(x).答案:f(x)>g(x)
2.若x,y均为正实数,判断x3+y3与x2y+xy2的大小关系.【解析】x3+y3-x2y-xy2=x2(x-y)-y2(x-y)=(x2-y2)(x-y)=(x-y)2(x+y),
因为x>0,y>0,所以(x-y)2(x+y)≥0,所以x3+y3≥x2y+xy2.
类型二 不等式性质的简单应用【典例】判断下列命题是否正确,并说明理由.(1)a>b>0,则 (2)c>a>b>0,则 (3)若 ,则ad>bc.(4)设a,b为正实数,若a-
【解析】(1)因为a>b>0,所以a>b两边同乘以得 得 > ,故正确.(2)因为c-a>0,c-b>0,且c-a
(3)由 ,所以 >0,即ad>bc且cd>0或ad
2.运用不等式的性质判断命题真假的三点注意事项(1)倒数法则要求两数同号.(2)两边同乘以一个数,不等号方向是否改变要视此数的正负而定.(3)同向不等式可以相加,异向不等式可以相减.
【变式训练】1.下列命题中正确的是_________ .①若a>b>0,c>d>0,那么 ②若a,b∈R,则a2+b2+5≥2(2a-b).
【解析】因为a>b>0,c>d>0,所以 >0,故 ①错误.a2+b2+5-2(2a-b)=a2+b2+5-4a+2b=(a-2)2+(b+1)2≥0,所以②正确.答案:②
2.若a
【证明】因为c
2.(变换条件、改变问法)本题中加上条件“e<0”,其他条件不变,证明: 【证明】因为c
【方法技巧】利用不等式性质证明简单不等式的实质与技巧(1)实质:就是根据性质把不等式进行变形,要注意不等式性质成立的条件.
(2)技巧:若不能直接由不等式性质得到,可先分析需要证明的不等式的结构.利用不等式的性质进行逆推,寻找使其成立的充分条件.
【变式训练】1.已知a>b>0,c>d>0.求证: 【证明】因为a>b>0,所以0< 因为c>d>0,所以0< 所以
所以 所以 即 又a,c,b,d均大于0,所以 所以
2.已知a>0,b>0,c>0,d>0,且 ,求证: 【证明】因为a>0,b>0,c>0,d>0且 ,所以ad>bc,所以ad+cd>bc+cd,即d(a+c)>c(b+d),所以
自我纠错 作差法比较大小【典例】设a+b>0,n为偶数, 的大小关系为_______________.
分析解题过程,找出错误之处,并写出正确答案.提示:n为偶数时,an-bn和an-1-bn-1不一定同号,这里忽略了在题设条件a+b>0且没有明确字母的具体值的情况下,要考虑分类讨论,即对a>0,b>0和a,b有一个负值的情况加以讨论.正确解答过程如下:
【解析】 (1)当a>0,b>0时,(an-bn)(an-1-bn-1)≥0,(ab)n>0,
(2)当a,b有一个为负数时,不妨设a>0,b<0,且a+b>0,所以a>|b|.又n为偶数,所以(an-bn)·(an-1-bn-1)>0,且(ab)n>0,
故 即 综合(1)(2)可知, 答案:
人教版新课标A选修4-5三 排序不等式评课课件ppt: 这是一份人教版新课标A选修4-5三 排序不等式评课课件ppt,共45页。PPT课件主要包含了失误案例等内容,欢迎下载使用。
高中数学人教版新课标A选修4-5一 二维形式的柯西不等式课文课件ppt: 这是一份高中数学人教版新课标A选修4-5一 二维形式的柯西不等式课文课件ppt,共50页。PPT课件主要包含了ac+bd2,失误案例等内容,欢迎下载使用。
高中人教版新课标A二 一般形式的柯西不等式背景图ppt课件: 这是一份高中人教版新课标A二 一般形式的柯西不等式背景图ppt课件,共43页。PPT课件主要包含了kbi,失误案例等内容,欢迎下载使用。













