
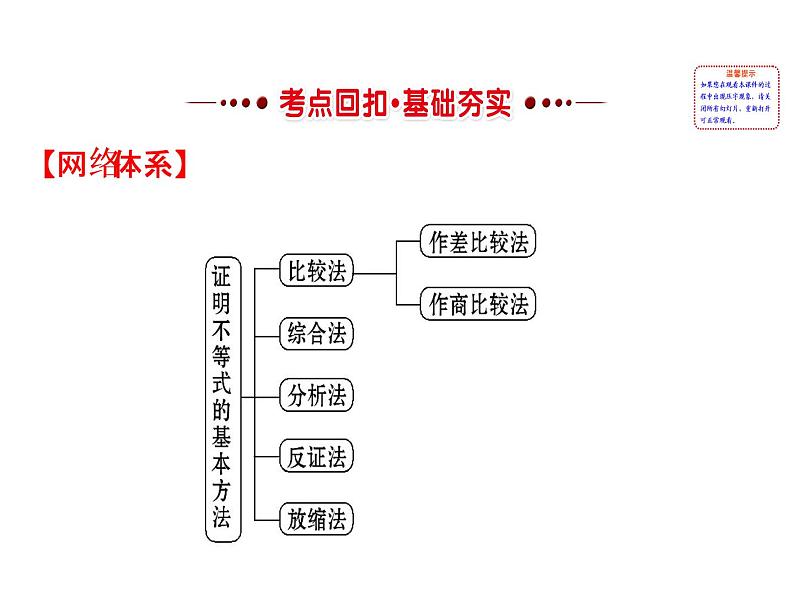





数学选修4-5第二讲 讲明不等式的基本方法综合与测试复习ppt课件
展开【核心速填】 1.比较法(1)作差比较法的依据:若a,b∈R,则______⇔a>b;a-b=0⇔a=b;______⇔a
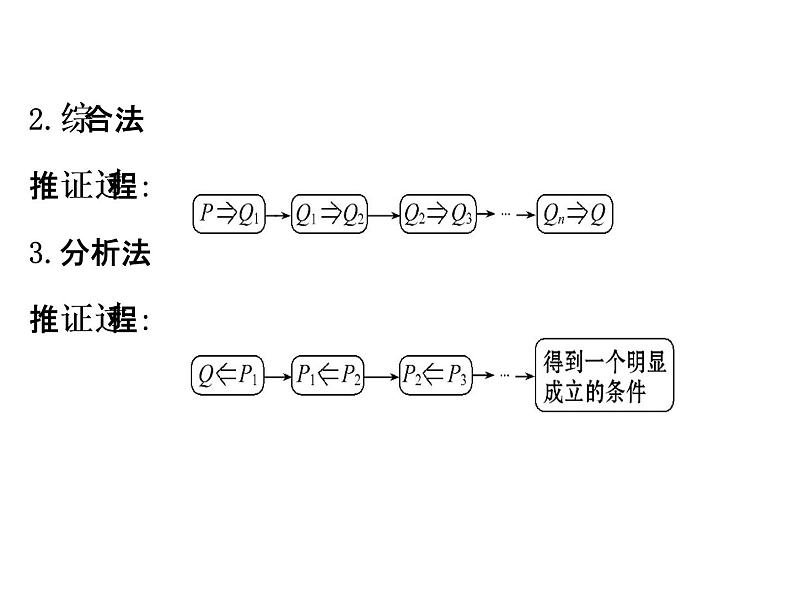
2.综合法推证过程: 3.分析法推证过程:
4.反证法反设→推理→矛盾→结论.5.放缩法分析待证式的形式特点,适当放大或缩小.
【易错警示】 (1)利用比较法证明不等式时,最后变形的结果要容易判断其符号,即变形为一个常数,或变形为若干个因式的乘积,或变形为一个或几个平方的和等.
(2)用分析法证明不等式时,一定要注意用好反推符号,或“要证明”“只需证明”“即证明”等词语.(3)用放缩法时,放缩要得当,不能“过大”也不能“过小”.
类型一 比较法证明不等式【典例1】设a≥b>0,求证:3a3+2b3≥3a2b+2ab2.【证明】3a3+2b3-(3a2b+2ab2)=3a2(a-b)+2b2(b-a)=(a-b)(3a2-2b2).因为a≥b>0,所以a-b≥0,3a2-2b2>2a2-2b2≥0.从而(3a2-2b2)(a-b)≥0,故3a3+2b3≥3a2b+2ab2成立.
【方法技巧】比较法证明不等式的依据及步骤(1)依据:不等式的意义及实数比较大小的充要条件.(2)一般步骤:①作差;②恒等变形;③判断结果的符号;
④下结论.其中,变形是证明推理中一个承上启下的关键,变形的目的在于判断差的符号,而不是考虑差能否化简或值是多少,变形所用的方法要具体情况具体分析,可以配方,可以因式分解,可以运用一切有效的恒等变形.
【变式训练】1.(2016·南阳高二检测)已知a,b是正实数,n是正整数.求证:(a+b)(an+bn)≤2(an+1+bn+1).【证明】(a+b)(an+bn)-2(an+1+bn+1)=an+1+abn+anb+bn+1-2an+1-2bn+1=abn+anb-an+1-bn+1=a(bn-an)+b(an-bn)=(a-b)(bn-an).
当a>b>0时,bn-an<0,a-b>0,此时(a-b)(bn-an)<0;当b>a>0时,bn-an>0,a-b<0,此时(a-b)(bn-an)<0;当a=b>0时,bn-an=0,a-b=0,此时(a-b)(bn-an)=0.综上所述:(a+b)(an+bn)-2(an+1+bn+1)≤0.即(a+b)(an+bn)≤2(an+1+bn+1).
2.(2016·福州高二检测)已知α∈(0,π),求证:2sin2α≤
【证明】2sin2α- =4sinαcsα-因为α∈(0,π),所以sinα>0,1-csα>0,又(2csα-1)2≥0,所以2sin2α- ≤0,所以2sin2α≤ .
类型二 综合法证明不等式【典例2】已知a>0,a2-2ab+c2=0且bc>a2,试证明:b>c.【证明】因为a2-2ab+c2=0,所以a2+c2=2ab.又a2+c2≥2ac,且a>0,所以2ab≥2ac,所以b≥c.若b=c,由a2-2ab+c2=0,得a2-2ab+b2=0,所以a=b.从而a=b=c,这与bc>a2矛盾.从而b>c.
【方法技巧】综合法证明不等式的依据、注意点及思考方向(1)依据:已知的不等式以及逻辑推证的基本理论.
(2)注意点:作为依据和出发点的几个重要不等式(已知或已证)成立的条件往往不同,应用时要先考虑是否具备应有的条件,避免错误,如一些带等号的不等式,应用时要清楚取等号的条件,即对重要不等式中“当且仅当……时,取等号”的理由要理解掌握.
(3)思考方向:综合法证明不等式的思考方向是“顺推”,即由已知的不等式出发,逐步推出其必要条件(由因导果),最后推导出所要证明的不等式成立.
【变式训练】1.(2016·昆明高二检测)已知a,b是不相等的正实数,求证:(a2b+a+b2)(ab2+a2+b)>9a2b2.【解题指南】因为a,b是不相等的正实数,所以a2b+a+b2及ab2+a2+b均可用三正数的均值不等式,从而用综合法可证明.
【证明】因为a,b是正实数,所以a2b+a+b2≥3 =3ab>0,(当且仅当a2b=a=b2即a=b=1时,等号成立);同理:ab2+a2+b≥3 =3ab>0,(当且仅当ab2=a2=b即a=b=1时,等号成立);
所以(a2b+a+b2)(ab2+a2+b)≥9a2b2,(当且仅当a=b=1时,等号成立);因为a≠b,所以(a2b+a+b2)(ab2+a2+b)>9a2b2.
2.若a,b,c都是正数,能确定 与的大小吗?【解析】能确定,因为a,b,c都是正数, +(b+c)≥4a, +(a+c)≥4b, +(a+b)≥4c,所以 ≥2(a+b+c),所以
类型三 分析法证明不等式【典例3】设a,b,c均为大于1的正数,且ab=10.求证:lgac+lgbc≥4lgc.
【证明】由于a>1,b>1,故要证明lgac+lgbc≥4lgc,只要证明 ≥4lgc.又c>1,故lgc>0,所以只要证 ≥4即 ≥4,因ab=10,故lga+lgb=1,只要证明 ≥4.(*)
由a>1,b>1,故lga>0,lgb>0,所以0
(2)思维方向:分析法证明不等式的思维方向是“逆推”,即由待证的不等式出发,逐步寻找使它成立的充分条件(执果索因),最后得到的充分条件是已知(或已证)的不等式.
(3)适用方法:当要证的不等式不知从何入手时,可考虑用分析法去证明,特别是对于条件简单而结论复杂的题目往往更为有效.
【变式训练】设f(x)=ax2+bx+c(a≠0),若函数y=f(x+1)与f(x)的图象关于y轴对称,求证: 为偶函数.
【证明】要证 为偶函数,只需证明其对称轴为x=0,即只需证 =0,只要证a=-b,由已知,抛物线f(x+1)的对称轴x= -1与对称轴x= 关于y轴对称,所以 -1= ,所以a=-b,所以 为偶函数.
类型四 反证法与放缩法证明不等式【典例4】已知0
由于0
2.放缩法将需要证明的不等式的值适当地放大(或缩小),使不等式由繁化简,达到证明的目的.
【变式训练】1.对于任何大于1的自然数n,证明:【证明】设a>b>0,m>0,则 所以
所以 所以
2.设Sn= 求证:不等式 对所有的正整数n都成立.
高考数学文科总复习选修4-5不等式的证明课件PPT: 这是一份高考数学文科总复习选修4-5不等式的证明课件PPT,共33页。PPT课件主要包含了选修4-5,不等式选讲,点击进入等内容,欢迎下载使用。
2022版高考数学一轮复习PPT课件:选修4-5(2)不等式的证明方法: 这是一份2022版高考数学一轮复习PPT课件:选修4-5(2)不等式的证明方法,共38页。PPT课件主要包含了栏目导航,课堂题型全突破,真题自主验效果,课前知识全通关,课后限时集训,ac+bd2,判断差的符号,A≥B,由因导果,充分条件等内容,欢迎下载使用。
2021届高中数学一轮复习 选修4-5 不等式选讲 第二节 证明不等式的基本方法 课件 (文数)(北师大版): 这是一份2021届高中数学一轮复习 选修4-5 不等式选讲 第二节 证明不等式的基本方法 课件 (文数)(北师大版),共7页。PPT课件主要包含了内容索引,定理性质,充分条件,和最小,积最大,一正二定三相等等内容,欢迎下载使用。













