高中数学人教版新课标A必修42.2 平面向量的线性运算随堂练习题

这是一份高中数学人教版新课标A必修42.2 平面向量的线性运算随堂练习题，共6页。试卷主要包含了理解向量减法的法则及其几何意义等内容，欢迎下载使用。
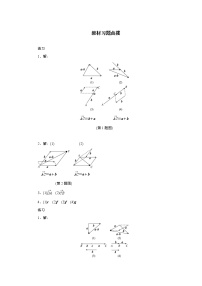
2.2.2　向量减法运算及其几何意义 课时目标　1.理解向量减法的法则及其几何意义.2.能运用法则及其几何意义，正确作出两个向量的差．向量的减法(1)定义：a－b＝a＋(－b)，即减去一个向量相当于加上这个向量的__________．(2)作法：在平面内任取一点O，作＝a，＝b，则向量a－b＝________.如图所示．(3)几何意义：如果把两个向量的始点放在一起，则这两个向量的差是以减向量的终点为________，被减向量的终点为________的向量．例如：－＝________.一、选择题1. 在如图四边形ABCD中，设＝a，＝b，＝c，则等于(　　)A．a－b＋cB．b－(a＋c)C．a＋b＋cD．b－a＋c2．化简－＋＋的结果等于(　　)A.        B.        C.        D.3．若O，E，F是不共线的任意三点，则以下各式中成立的是(　　)A.＝＋          B.＝－C.＝－＋        D.＝－－4．在平行四边形ABCD中，|＋|＝|－|，则有(　　)A. ＝0               B. ＝0或＝0C．ABCD是矩形         D．ABCD是菱形5．若||＝5，||＝8，则||的取值范围是(　　)A．[3,8]         B．(3,8)C．[3,13]        D．(3,13)6．边长为1的正三角形ABC中，|－|的值为(　　)A．1        B．2        C.        D.题　号123456答　案      二、填空题7. 如图所示，在梯形ABCD中，AD∥BC，AC与BD交于O点，则－－＋＋＝________.8．化简(－)－(－)的结果是________．9. 如图所示，已知O到平行四边形的三个顶点A、B、C的向量分别为a，b，c，则＝____________(用a，b，c表示)．10．已知非零向量a，b满足|a|＝＋1，|b|＝－1，且|a－b|＝4，则 |a＋b|＝________. 三、解答题11. 如图所示，O是平行四边形ABCD的对角线AC、BD的交点，设＝a，＝b，＝c，求证：b＋c－a＝.       12. 如图所示，已知正方形ABCD的边长等于1，＝a，＝b，＝c，试作出下列向量并分别求出其长度，(1)a＋b＋c；　(2)a－b＋c.         能力提升13．在平行四边形ABCD中，＝a，＝b，先用a，b表示向量和，并回答：当a，b分别满足什么条件时，四边形ABCD为矩形、菱形、正方形？               14．如图所示，O为△ABC的外心，H为垂心，求证：＝＋＋.            1．向量减法的实质是向量加法的逆运算．利用相反向量的定义，－＝就可以把减法转化为加法．即：减去一个向量等于加上这个向量的相反向量．如a－b＝a＋(－b)．2．在用三角形法则作向量减法时，要注意“差向量连接两向量的终点，箭头指向被减数”．解题时要结合图形，准确判断，防止混淆．3．以向量＝a、＝b为邻边作平行四边形ABCD，则两条对角线的向量为＝a＋b，＝b－a，＝a－b，这一结论在以后应用非常广泛，应该加强理解并记住． 2．2.2　向量减法运算及其几何意义答案知识梳理(1)相反向量　(2)　(3)始点　终点　作业设计1．A　2.B　3.B4．C　[＋与－分别是平行四边形ABCD的两条对角线，且|＋|＝|－|，∴ABCD是矩形．]5．C　[∵||＝|－|且|||－|||≤|－|≤|A|＋||.∴3≤|－|≤13.∴3≤||≤13.]6．D　[如图所示，延长CB到点D，使BD＝1，连结AD，则－＝＋＝＋＝.在△ABD中，AB＝BD＝1，∠ABD＝120°，易求AD＝，∴|－|＝.]7.8．0解析　方法一　(－)－(－)＝－－＋＝＋＋＋＝(＋)＋(＋)＝＋＝0.方法二　(－)－(－)＝－－＋＝(－)＋(－)＝＋＝0.9．a－b＋c解析　＝＋＝＋＝＋－＝a＋c－b＝a－b＋c.10．4解析　如图所示．设O＝a，O＝b，则|B|＝|a－b|.以OA与OB为邻边作平行四边形OACB，则|O|＝|a＋b|.由于(＋1)2＋(－1)2＝42.故|O|2＋|O|2＝|B|2，所以△OAB是∠AOB为90°的直角三角形，从而OA⊥OB，所以▱OACB是矩形，根据矩形的对角线相等有|O|＝|B|＝4，即|a＋b|＝4.11．证明　方法一　∵b＋c＝＋＝＋＝，＋a＝＋＝，∴b＋c＝＋a，即b＋c－a＝.方法二　∵c－a＝－＝－＝，＝＋＝－b，∴c－a＝－b，即b＋c－a＝.12．解　(1)由已知得a＋b＝＋＝，又＝c，∴延长AC到E，使||＝||.则a＋b＋c＝，且||＝2.∴|a＋b＋c|＝2.(2)作＝，连接CF，则＋＝，而＝－＝a－＝a－b，∴a－b＋c＝＋＝且||＝2.∴|a－b＋c|＝2.13．解　由向量加法的平行四边形法则，得＝a＋b，＝－＝a－b.则有：当a，b满足|a＋b|＝|a－b|时，平行四边形两条对角线相等，四边形ABCD为矩形；当a，b满足|a|＝|b|时，平行四边形的两条邻边相等，四边形ABCD为菱形；当a，b满足|a＋b|＝|a－b|且|a|＝|b|时，四边形ABCD为正方形．14．证明　作直径BD，连接DA、DC，则＝－，DA⊥AB，AH⊥BC，CH⊥AB，CD⊥BC.∴CH∥DA，AH∥DC，故四边形AHCD是平行四边形．∴＝，又＝－＝＋，∴＝＋＝＋＝＋＋.