高中人教版新课标A第一章 导数及其应用1.1变化率与导数第2课时综合训练题

预习导航

1．导数的几何意义

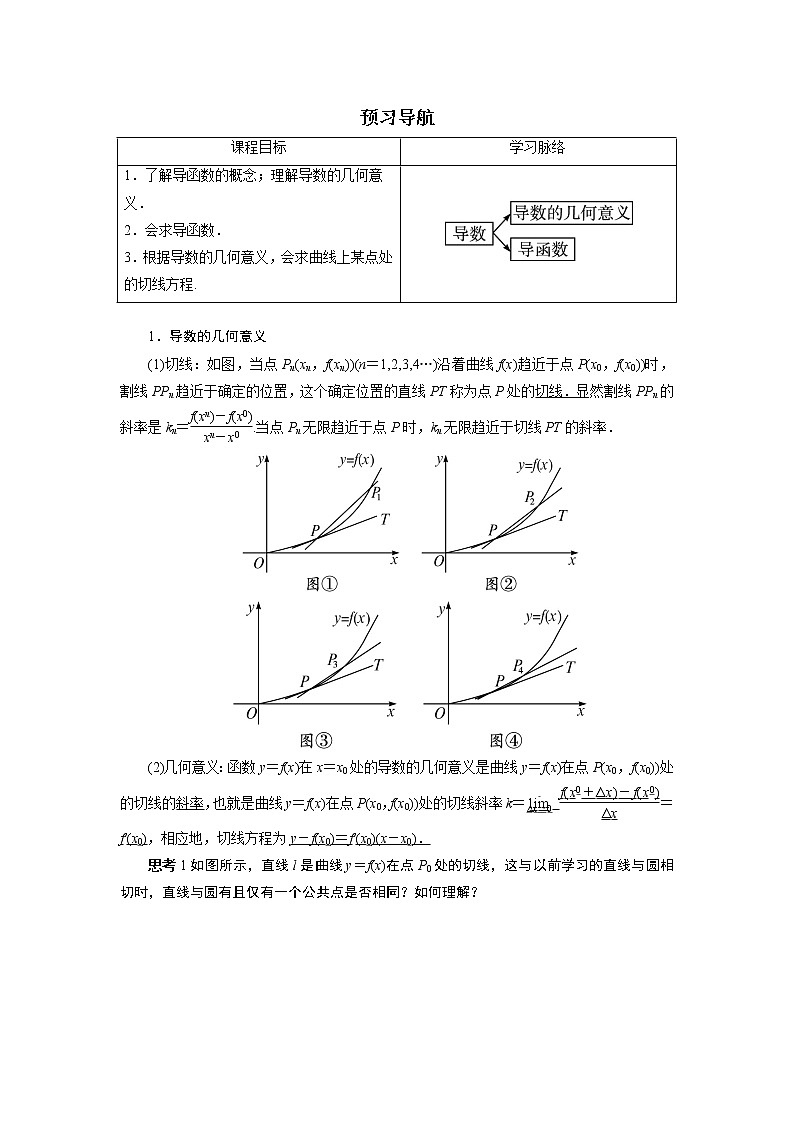
(1)切线：如图，当点Pn(xn，f(xn))(n＝1,2,3,4…)沿着曲线f(x)趋近于点P(x0，f(x0))时，割线PPn趋近于确定的位置，这个确定位置的直线PT称为点P处的切线．显然割线PPn的斜率是kn＝.当点Pn无限趋近于点P时，kn无限趋近于切线PT的斜率．

(2)几何意义：函数y＝f(x)在x＝x0处的导数的几何意义是曲线y＝f(x)在点P(x0，f(x0))处的切线的斜率，也就是曲线y＝f(x)在点P(x0，f(x0))处的切线斜率k＝ ＝f′(x0)，相应地，切线方程为y－f(x0)＝f′(x0)(x－x0)．

思考1如图所示，直线l是曲线y＝f(x)在点P0处的切线，这与以前学习的直线与圆相切时，直线与圆有且仅有一个公共点是否相同？如何理解？

提示：不相同．曲线y＝f(x)在某点处的切线只是在切点P0附近区域上只有一个公共点，但放眼大的范围公共点可能不只一个，甚至多个．因此，直线l是曲线y＝f(x)在切点P0处的切线，但在点A处不是曲线的切线．

2．导函数

从求函数f(x)在x＝x0处导数的过程可以看到，当x＝x0时，f′(x0)是一个确定的数．这样，当x变化时，f′(x)便是x的一个函数，我们称它为f(x)的导函数(简称导数)．

y＝f(x)的导函数有时也记作y′，

即f′(x)＝y′＝ .

思考2如何区分f′(x0)与f′(x)?

提示：