

高考数学真题专项练习 专题01 集合概念与运算(解析版)
展开大数据分析*预测高考
十年试题分类*探求规律
考点1 集合的含义与表示
1.【2020年高考全国Ⅲ卷文数1】已知集合,,则A∩B中元素的个数为( )
A.2B.3C.4D.5
【答案】B【解析】由题意,,故中元素的个数为3,故选B
2.【2020年高考全国Ⅲ卷理数1】已知集合,,则中元素的个数为( )
A.2B.3C.4D.6
【答案】C【解析】由题意,中的元素满足,且,由,得,
所以满足的有,故中元素的个数为4.故选C.
3.【2017新课标3,理1】已知集合A=,B=,则AB中元素的个数为
A.3B.2C.1D.0
【答案】B【解析】由题意可得,圆 与直线 相交于两点,,则中有两个元素,故选B.
4.【2018新课标2,理1】已知集合A=x , yx2+y2≤3 , x∈Z , y∈Z,则A中元素的个数为( )
A.9 B.8 C.5 D.4
【答案】A【解析】∵x2+y2≤3,∴x2≤3,∵x∈Z,∴x=−1,0,1,当x=−1时,y=−1,0,1;当x=0时,y=−1,0,1;当x=−1时,y=−1,0,1;所以共有9个,选A.
5.【2013山东,理1】已知集合A={0,1,2},则集合B=中元素的个数是
A.1 B.3 C.5 D.9
【答案】C【解析】;;
.∴中的元素为共5个,故选C.
6.【2013江西,理1】若集合中只有一个元素,则=
A.4 B.2 C.0 D.0或4
【答案】A【解析】当时,不合,当时,,则,故选A.
7.【2012江西,理1】若集合,,则集合中的元素的个数为( )
A.5 B.4 C.3 D.2
【答案】C【解析】根据题意,容易看出只能取1,1,3等3个数值.故共有3个元素,故选C.
8.【2011广东,理1】已知集合A=为实数,且,B=为实数,且,则AB的元素个数为
A.4 B.3 C.2 D.1
【答案】C【解析】由消去,得,解得或,这时或,即,有2个元素.
9.【2011福建,理1】是虚数单位,若集合={-1,0,1},则
A.∈ B.∈ C.∈ D. ∈
【答案】B【解析】∵=-1∈,故选B.
10.【2012天津,文9】集合中的最小整数为_______.
【答案】【解析】不等式,即,,所以集合,所以最小的整数为.
考点2 集合间关系
【试题分类与归纳】
1.【2012新课标,文1】已知集合,,则
A. B. C. D.
【答案】B【解析】A=(-1,2),故B eq \(,)A,故选B.
2.【2012新课标卷1,理1】已知集合A={x|x2-2x>0},B={x|- eq \r(5)<x< eq \r(5)},则 ( )
A、A∩B= B、A∪B=R C、B⊆AD、A⊆B
【答案】B【解析】A=(-,0)∪(2,+),∴A∪B=R,故选B.
3.【2015重庆,理1】已知集合,,则
A.A=B B. C. D.
【答案】D【解析】由于,故A、B、C均错,D是正确的,选D.
4.【2012福建,理1】已知集合,,下列结论成立的是( )
A. B. C.D.
【答案】D【解析】由M={1,2,3,4},N={2,2},可知2∈N,但是2M,则NM,故A错误.∵MN={1,2,3,4,2}≠M,故B错误.M∩N={2}≠N,故C错误,D正确.故选D
5.【2011浙江,理1】若,则( )
A. B. C. D.
【答案】D【解析】 ∴,又∵,∴,故选D.
6.【2011北京,理1】已知集合=,.若,则的取值范围是
A.(∞,1] B.[1,+∞) C.[1,1] D.(∞,1] [1,+∞)
【答案】C【解析】因为,所以,即,得,解得,
所以的取值范围是.
7.【2013新课标1,理1】已知集合A={x|x2-2x>0},B={x|- eq \r(5)<x< eq \r(5)=,则( )
A.A∩B=B.A∪B=R C.B⊆AD.A⊆B
【答案】B【解析】A=(-,0)∪(2,+),∴A∪B=R,故选B.
8.【2012大纲,文1】已知集合={︱是平行四边形},={︱是矩形},={︱是正方形},={︱是菱形},则
. . . .
【答案】B【解析】∵正方形一定是矩形,∴是的子集,故选.
9.【2012年湖北,文1】已知集合,,则满足条件的集合C的个数为( )
A.1 B.2 C.3 D.4
【答案】D【解析】求解一元二次方程,,易知.因为,所以根据子集的定义,集合必须含有元素1,2,且可能含有元素3,4,原题即求集合的子集个数,即有个.故选D.
考点3 集合间的基本运算
【试题分类与归纳】
1.【2011课标,文1】 已知集合M={0,1,2,3,4},N={1,3,5},P=M∩N,则P的子集共有
(A)2个 (B)4个 (C)6个 (D)8个
【答案】B【解析】∵P=M∩N={1,3}, ∴P的子集共有=4,故选B.
2.【2013新课标2,理1】已知集合M={∈R|},N={-1,0,1,2,3},则M∩N=
A.{0,1,2} B.{-1,0,1,2} C.{-1,0,2,3} D.{0,1,2,3}
【答案】A【解析】M=(-1,3),∴M∩N={0,1,2},故选A.
3.【2013新课标2,文1】已知集合M={x|-3
【答案】C【解析】因为集合M=,所以M∩N={0,-1,-2},故选C.
4.【2013新课标I,文1】已知集合A={1,2,3,4},,则A∩B=( )
(A){1,4}(B){2,3}(C){9,16}(D){1,2}
【答案】A;【解析】依题意,,故.
5.【2014新课标1,理1】已知集合A={|},B={|-2≤<2},则=
.[-2,-1] .[-1,2) .[-1,1] .[1,2)
【答案】A【解析】∵A=,∴=[-2,-1],故选A.
6.【2014新课标2,理1】设集合M={0,1,2},N=,则=( )
A.{1} B.{2} C.{0,1} D.{1,2}
【答案】D【解析】∵,∴,故选D.
7.【2014新课标1,文1】已知集合=,=则( )
B. C. D.
【答案】B【解析】(-1,1),故选B.
8.【2014新课标2,文1】设集合,则( )
B. C. D.
【答案】B【解析】∵,∴.
9.【2015新课标2,理1】已知集合,,则( )
A. B. C. D.
【答案】A【解析】由题意知,,∴,故选A.
10.【2015新课标1,文1】已知集合,则集合中的元素个数为( )
(A) 5 (B)4 (C)3 (D)2
【答案】D
【解析】由条件知,当n=2时,3n+2=8,当n=4时,3n+2=14,故A∩B={8,14},故选D.
11.【2015新课标2,文1】已知集合,,则( )
A. B. C. D.
【答案】A【解析】由题知,,故选A.
12.【2016新课标1,理1】设集合,,则=
(A)(B)(C)(D)
【答案】D【解析】由题知=(1,3),B=,所以=,故选D.
13.【2016新课标2,理2】已知集合,,则( )
(A) (B) (C) (D)
【答案】C【解析】由题知={0,1},所以{0,1,2,3},故选C.
14.【2016新课标3,理1】设集合,则=
(A) [2,3] (B)(-,2] [3,+)
(C) [3,+) (D)(0,2] [3,+)
【答案】D【解析】由题知,,∴=(0,2] [3,+),故选D.
15.【2016新课标2,文1】已知集合,则( )
(A)(B)(C) (D)
【答案】D【解析】由题知,,∴,故选D.
16.【2016新课标1,文1】设集合,,则( )
(A){1,3}(B){3,5}(C){5,7}(D){1,7}
【答案】B【解析】由题知,,故选B.
17.【2016新课标3,文1】设集合,则=
(A) (B)(C)(D)
【答案】C【解析】由题知,,故选C.
18.【2017新课标1,理1】已知集合A={x|x<1},B={x|},则
A.B.
C.D.
【答案】A【解析】由题知,,∴,故选A.
19.【2017新课标1,文1】已知集合A=,B=,则( )
A.AB=B.AB
C.ABD.AB=R
【答案】A
20.【2017新课标2,理2】设集合,.若,则( )
A. B. C. D.
【答案】C【解析】由得,所以,,故选C.
21.【2017新课标2,文1】设集合则( )
A. B. C. D.
【答案】A【解析】由题意,故选A.
22.【2017新课标3,文1】已知集合A={1,2,3,4},B={2,4,6,8},则AB中元素的个数为( )
A.1B.2C.3D.4
【答案】B【解析】由题意可得,,故选B.
23.【2018新课标1,理1】已知集合A=xx2−x−2>0,则∁RA=
A.x−1
【答案】B【解析】由题知,A=x|x<−1或x>2,∴CRA=x|−1≤x≤2,故选B.
24.【2018新课标3,理1】已知集合A=x|x−1≥0,B=0 , 1 , 2,则A∩B=
A.0 B.1 C.1 , 2 D.0 , 1 , 2
【答案】C【解析】由题意知,A={x≥1},所以A∩B={1,2},故选C.
25.【2018新课标1,文1】已知集合,,则( )
A. B. C. D.
【答案】A【解析】根据集合交集中元素的特征,可以求得,故选A.
26.【2018新课标2,文1】已知集合,,则
A. B. C. D.
【答案】C【解析】,故选C
27.【2019新课标1,理1】已知集合,则=( )
A.B.
C.D.
【答案】C【解析】由题意得,,则
.故选C.
28.【2019新课标1,文2】已知集合,则=( )
A. B. C.D.
【答案】C【解析】由已知得,所以,故选C.
29.【2019新课标2,理1】设集合A={x|x2-5x+6>0},B={ x|x-1<0},则A∩B=
A.(-∞,1) B.(-2,1) C.(-3,-1) D.(3,+∞)
【答案】A【解析】由题意得,,则.故选A.
30.【2019新课标2,文1】.已知集合,,则A∩B=
A.(–1,+∞)B.(–∞,2)
C.(–1,2)D.
【答案】C【解析】由题知,,故选C.
31.【2019新课标3,理1】已知集合,则( )
A.B. C. D.
【答案】A【解析】由题意得,,则.故选A.
32.【2019浙江,1】已知全集,集合,,则=
A.B.C.D.
【答案】A【解析】 QUOTE ∵∁UA={-1,3} ,.故选A.
33.【2019天津,理1】设集合,则
A. B. C. D.
【答案】D【解析】由题知,,所以,故选D.
34.【2011辽宁,理1】已知M,N为集合I的非空真子集,且M,N不相等,若,则
A.M B.N C.I D.
【答案】A【解析】根据题意可知,是的真子集,所以.
35.【2018天津,理1】设全集为R,集合,,则
A. B. C. D.
【答案】B【解析】因为,所以,因为,
所以,故选B.
36.【2017山东,理1】设函数的定义域,函数的定义域为,则( )
A. B. C. D.
【答案】D【解析】由得,由得,故,选D.
37.【2017天津,理1】设集合,,,
则
A. B. C. D.
【答案】B【解析】,选B.
38.【2017浙江,理1】已知集合,,那么=
A. B. C. D.
【答案】A【解析】由题意可知,选A.
39.【2016年山东,理1】设集合 则=
A. B. C. D.
【答案】C【解析】集合表示函数的值域,故.由,得,故,所以.故选C.
40.【2016年天津,理1】已知集合则=
A.B.C.D.
【答案】D【解析】由题意,所以,故选D.
41.【2015浙江,理1】已知集合,则
A. B. C. D.
【答案】C【解析】,故,故选C.
42.【2015四川,理1】设集合,集合,则
A. B.
C. D.
【答案】A【解析】,,∴.
43.【2015福建,理1】若集合(是虚数单位),,则等于( )
A. B. C. D.
【答案】C【解析】由已知得,故,故选C.
44.【2015广东,理1】若集合,,
则
A. B. C. D.
【答案】D 【解析】 由得或,得.
由 得或,得.显然.
45.【2015陕西,理1】设集合,,则
A. B. C. D.
【答案】A【解析】,,
所以,故选A.
46.【2015天津,理1】已知全集,集合,集合
,则集合
A. B. C. D.
【答案】A【解析】,所以,故选A.
47.【2014山东,理1】设集合则
A.[0,2] B.(1,3) C.[1,3) D.(1,4)
【答案】B【解析】∵,∴,故选B.
48.【2014浙江,理1】设全集,集合,则
A. B. C. D.
【答案】B【解析】由题意知,,所以,选B.
49.【2014辽宁,理1】已知全集,则集合
A. B. C. D.
【答案】D【解析】由已知得,或,故,故选D.
50.【2013山东,】已知集合均为全集的子集,且,
,则
{3} B.{4} C.{3,4} D.
【答案】A【解析】由题意,且,所以中必有3,没有4,
,故.
51.【2013陕西,理1】设全集为R,函数的定义域为M,则为
A.[-1,1] B.(-1,1) C. D.
【答案】D【解析】的定义域为M=[1,1],故=,选D.
52.【2013湖北,理1】已知全集为,集合,,则( )
A. B.
C. D.
【答案】C【解析】,,.
53.【2011江西,理1】若全集,则集合等于
A. B. C. D.
【答案】D【解析】因为,所以==.
54.【2011辽宁】已知M,N为集合I的非空真子集,且M,N不相等,若,则
A.M B.N C.I D.
【答案】A【解析】根据题意可知,是的真子集,所以.
55.【2017江苏】已知集合,,若,则实数的值为_.
【答案】1【解析】由题意,显然,此时,满足题意,故.
56.【2020年高考全国Ⅰ卷文数1】已知集合则( )
A. B. C. D.
【答案】D【解析】由解得,所以,又因为,所以,故选D.
57.【2020年高考全国I卷理数2】设集合A={x|x2–4≤0},B={x|2x+a≤0},且A∩B={x|–2≤x≤1},则a=( )
A.–4B.–2C.2D.4
【答案】B【解析】求解二次不等式可得:,求解一次不等式可得:.由于,故:,解得:.故选B.
58.【2020年高考全国II卷文数1】已知集合A={x||x|<3,x∈Z},B={x||x|>1,x∈Z},则A∩B=( )
A. B.{–3,–2,2,3) C.{–2,0,2} D.{–2,2}
【答案】D【解析】因为,或,所以.故选D.
59.【2020年高考全国II卷理数1】已知集合,则( )
A. B. C. D.
【答案】A【解析】由题意可得:,则.故选A.
60.【2020年高考浙江卷1】已知集合P=, 则PQ= ( )
A. B. C. D.
【答案】B【解析】由已知易得,故选B.
61.【2020年高考北京卷1】已知集合,则
A. B. C.D.
【答案】D【详解】,故选D.
62.【2020年高考山东卷1】设集合,,则
A. B. C.D.
【答案】C【详解】,故选C.
63.【2020年高考天津卷1】设全集,集合,则( )
A.B.C.D.
【答案】C【解析】由题意结合补集的定义可知:,则,故选C.
64.【2020年高考上海卷1】已知集合,则 .
【答案】【解析】由交集定义可知,故答案为:.
65.【2020年高考江苏卷1】已知集合,则 .
【答案】【解析】由题知,.
考点4 与集合有关的创新问题
1.(2012课标,理1).已知集合={1,2,3,4,5},={(,)|∈,∈,∈},则中所含元素的个数为( )
.3 .6 .8 .10
【答案】D.【解析】={(2,1),(3,1),(4,1),(5,1),(3,2),(4,2),(5,2),(4,3),(5,3),(5,4)},含10个元素,故选D.
2.【2015湖北】已知集合,
,定义集合,则中元素的个数为( )
A.77 B.49 C.45 D.30
【答案】C【解析】因为集合,所以集合中有9个元素(即9个点),即图中圆中的整点,集合中有25个元素(即25个点):即图中正方形中的整点,集合
的元素可看作正方形中的整点(除去四个顶点),即个.
3.【2013广东,理8】设整数,集合,令集合,且三条件恰有一个成立,若和都在中,则下列选项正确的是
A., B., C., D.,
【答案】B 【解析】特殊值法,不妨令,,则,
,故选B.
如果利用直接法:因为,,所以…①,…②,…③三个式子中恰有一个成立;…④,…⑤,…⑥三个式子中恰有一个成立.配对后只有四种情况:第一种:①⑤成立,此时,于是,;第二种:①⑥成立,此时,于是,;第三种:②④成立,此时,于是,;第四种:③④成立,此时,于是,.综合上述四种情况,可得,.
4.【2012福建,文12】在整数集Z中,被5除所得余数为k的所有整数组成一个“类”,记为[k],即[k]={丨∈Z},k=0,1,2,3,4.给出如下四个结论:
①2011∈[1];②-3∈[3];③Z=[0]∪[1]∪[2]∪[3]∪[4];④“整数,属于同一“类”的充要条件是“∈[0]”.其中正确的结论个数是( )
A.1 B.2 C.3 D.4
【答案】C【解析】①2011=2010+1=402×5+1∈[1],正确;由-3=-5+2∈[2]可知②不正确;根据题意信息可知③正确;若整数,属于同一类,不妨设,∈[k]={丨n∈Z},则=5n+k,=5m+k,n,m为整数,=5(n-m)+0∈[0]正确,故①③④正确,答案应选C.
5.【2013浑南,文15】对于E={}的子集X={},定义X的“特征数列”为,其中 ,其余项均为0,例如子集{}的“特征数列”为0,1,1,0,0,…,0
子集{}的“特征数列”的前三项和等于 ;
若E的子集P的“特征数列” 满足,,1≤≤99;
E 的子集Q的“特征数列” 满足,,1≤≤98,则P∩Q的元素个数为_________.
【解析】 (1) 子集{}的特征数列为:1,0,1,0,1,0,0,0……0.所以前3项和等于1+0+1=2.
(2)∵E的子集P的“特征数列” 满足,,1≤≤99;
∴P的“特征数列”:1,0,1,0 … 1,0. 所以P = .
∵E 的子集Q的“特征数列” 满足,,1≤≤98,,可知:j=1时,=1,∵,∴==0;同理=1==…=.Q的“特征数列”:1,0,0,1,0,0 …1,0,0,1.所以Q = .
∴ ,∵97=1+(17-1)×6,∴共有17个相同的元素.
7.【2018北京,理20】设为正整数,集合.对于集合中的任意元素和,记
.
(1)当时,若,,求和的值;
(2)当时,设是的子集,且满足:对于中的任意元素,当相同时,是奇数;当不同时,是偶数.求集合中元素个数的最大值;
(3)给定不小于2的,设是的子集,且满足:对于中的任意两个不同的元素,.写出一个集合,使其元素个数最多,并说明理由.
【解析】(1)因为,,所以
,
.
(2)设,则.
由题意知,,,∈{0,1},且为奇数,
所以,,,中1的个数为1或3.
所以B{(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1),(0,1,1,1),(1,0,1,1),(1,1,0,1),(1,1,1,0)}.
将上述集合中的元素分成如下四组:
(1,0,0,0),(1,1,1,0);(0,1,0,0),(1,1,0,1);(0,0,1,0),(1,0,1,1);(0,0,0,1),(0,1,1,1).
经验证,对于每组中两个元素,,均有.
所以每组中的两个元素不可能同时是集合的元素.
所以集合中元素的个数不超过4.
又集合{(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1)}满足条件,
所以集合中元素个数的最大值为4.
(3)设,
,则.
对于()中的不同元素,,经验证,.
所以()中的两个元素不可能同时是集合的元素.
所以中元素的个数不超过.
取且().
令,则集合的元素个数为,且满足条件.
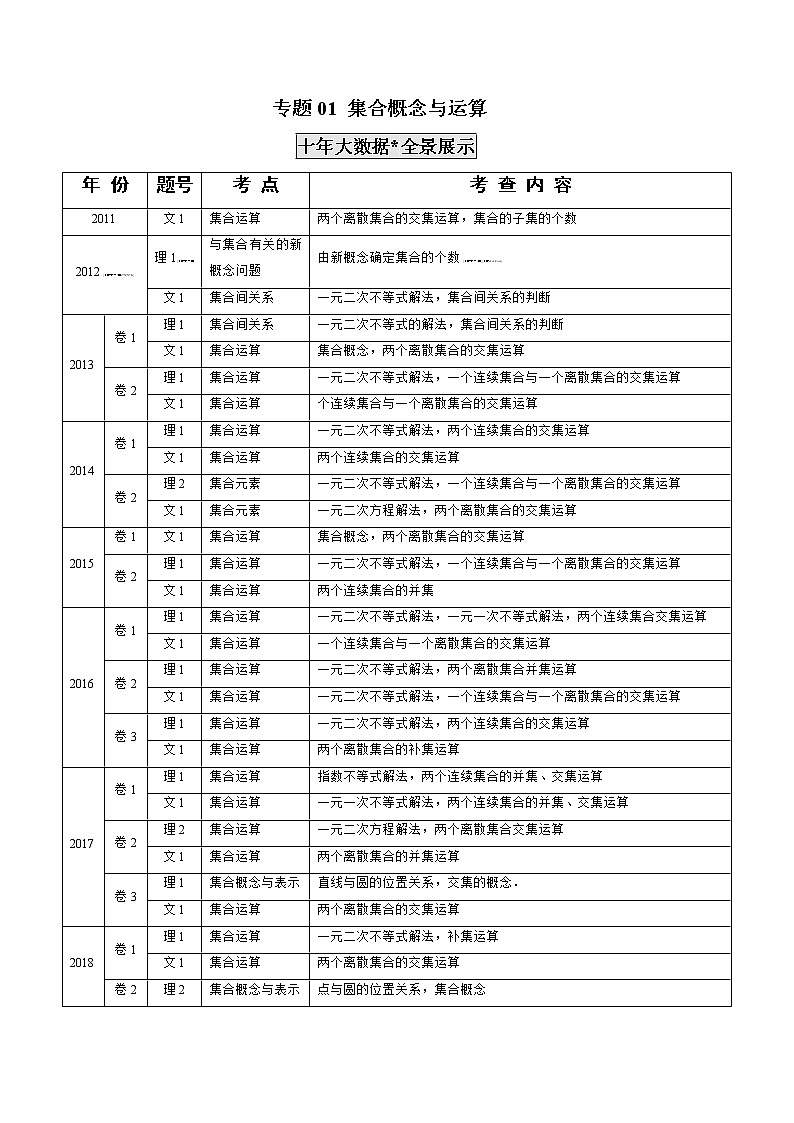
故是一个满足条件且元素个数最多的集合.年 份
题号
考 点
考 查 内 容
2011
文1
集合运算
两个离散集合的交集运算,集合的子集的个数
2012[来源:学*科*网Z*X*X*K]
理1
与集合有关的新概念问题
由新概念确定集合的个数
文1
集合间关系
一元二次不等式解法,集合间关系的判断
2013
卷1
理1
集合间关系
一元二次不等式的解法,集合间关系的判断
文1
集合运算
集合概念,两个离散集合的交集运算
卷2
理1
集合运算
一元二次不等式解法,一个连续集合与一个离散集合的交集运算
文1
集合运算
个连续集合与一个离散集合的交集运算
2014
卷1
理1
集合运算
一元二次不等式解法,两个连续集合的交集运算
文1
集合运算
两个连续集合的交集运算
卷2
理2
集合元素
一元二次不等式解法,一个连续集合与一个离散集合的交集运算
文1
集合元素
一元二次方程解法,两个离散集合的交集运算
2015
卷1
文1
集合运算
集合概念,两个离散集合的交集运算
卷2
理1
集合运算
一元二次不等式解法,一个连续集合与一个离散集合的交集运算
文1
集合运算
两个连续集合的并集
2016
卷1
理1
集合运算
一元二次不等式解法,一元一次不等式解法,两个连续集合交集运算
文1
集合运算
一个连续集合与一个离散集合的交集运算
卷2
理1
集合运算
一元二次不等式解法,两个离散集合并集运算
文1
集合运算
一元二次不等式解法,一个连续集合与一个离散集合的交集运算
卷3
理1
集合运算
一元二次不等式解法,两个连续集合的交集运算
文1
集合运算
两个离散集合的补集运算
2017
卷1
理1
集合运算
指数不等式解法,两个连续集合的并集、交集运算
文1
集合运算
一元一次不等式解法,两个连续集合的并集、交集运算
卷2
理2
集合运算
一元二次方程解法,两个离散集合交集运算
文1
集合运算
两个离散集合的并集运算
卷3
理1
集合概念与表示
直线与圆的位置关系,交集的概念.
文1
集合运算
两个离散集合的交集运算
2018
卷1
理1
集合运算
一元二次不等式解法,补集运算
文1
集合运算
两个离散集合的交集运算
卷2
理2
集合概念与表示
点与圆的位置关系,集合概念
文1
集合运算
两个离散集合的交集运算
卷3
文理1
集合运算
一元一次不等式解法,一个连续集合与一个离散集合的交集运算
2019
卷1
理1
集合运算
一元二次不等式解法,两个连续集合的交集运算
文2
集合运算
三个离散集合的补集、交集运算
卷2
理1
集合运算
一元二次不等式解法,一元一次不等式解法,两个连续集合的交集运算
文1
集合运算
两个连续集合的交集运算
卷3
文理1
集合运算
一元二次不等式解法,一个连续集合与一个离散集合的交集运算
2020
卷1
理2
集合运算
一元二次不等式的解法,含参数的一元一次不等式的解法,利用集合的交集运算求参数的值
文1
集合运算
一元二次不等式解法,一个连续集合与一个离散集合的交集运算
卷2
理1
集合运算
两个离散集合的并集、补集运算
文1
集合运算
绝对值不等式的解法,一个连续集合与一个离散集合的交集运算
卷3
理1
集合运算
二元一次方程及二元一次不等式混合组的整数解的解法,一个连续集合与一个离散集合的交集运算
文1
集合运算
一个连续集合与一个离散集合的交集运算
考点
出现频率
2021年预测
集合的含义与表示
37次考2次
在理科卷中可能考查本考点
集合间关系
37次考2次
可能在试卷中考查两个几何关系的判定或子集的个数问题
集合间运算
37次考32次
常与一元二次不等式解法、一元一次不等式解法、指数、对数不等式解法结合重点考查集合的交集运算,也可能考查集合的并集、补集运算
与集合有关的创新问题
37次考1次
考查与集合有关的创新问题可能性不大
专题01 集合及其运算-2023年高考数学真题专题汇编(新高考卷): 这是一份专题01 集合及其运算-2023年高考数学真题专题汇编(新高考卷),文件包含专题01集合及其运算原卷版docx、专题01集合及其运算解析版docx等2份试卷配套教学资源,其中试卷共28页, 欢迎下载使用。
2011-2020年高考数学真题分专题训练 专题01 集合概念与运算(教师版含解析): 这是一份2011-2020年高考数学真题分专题训练 专题01 集合概念与运算(教师版含解析),共16页。试卷主要包含了故选C,【2013 江西,理1】若集合等内容,欢迎下载使用。
高中数学高考专题01 集合概念与运算(原卷版): 这是一份高中数学高考专题01 集合概念与运算(原卷版),共11页。












