初中数学人教版八年级下册18.2.2 菱形教学ppt课件

这是一份初中数学人教版八年级下册18.2.2 菱形教学ppt课件，共23页。PPT课件主要包含了复习巩固，新课导入，重难点解析，随堂检测，旧知回顾，平行四边形，菱形的性质，想一想，菱形的判定定理，数学语言等内容，欢迎下载使用。

前面我们学习了平行四边形和矩形，知道如果平行四边形有一个角是直角时，称为什么图形？
如果从边的角度，将平行四边形特殊化，又会得到什么特殊的四边形呢？
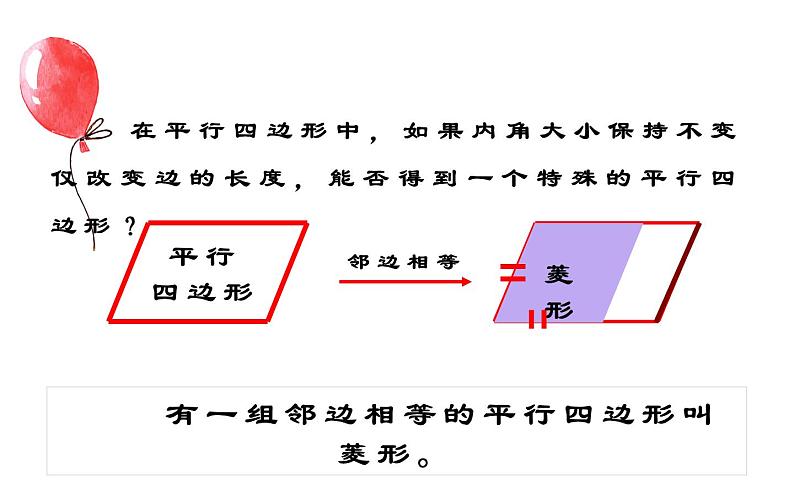
在平行四边形中，如果内角大小保持不变仅改变边的长度，能否得到一个特殊的平行四边形？
有一组邻边相等的平行四边形叫菱形。
菱形具有工整，匀称，美观等许多优点，常被人们用在图案设计上。
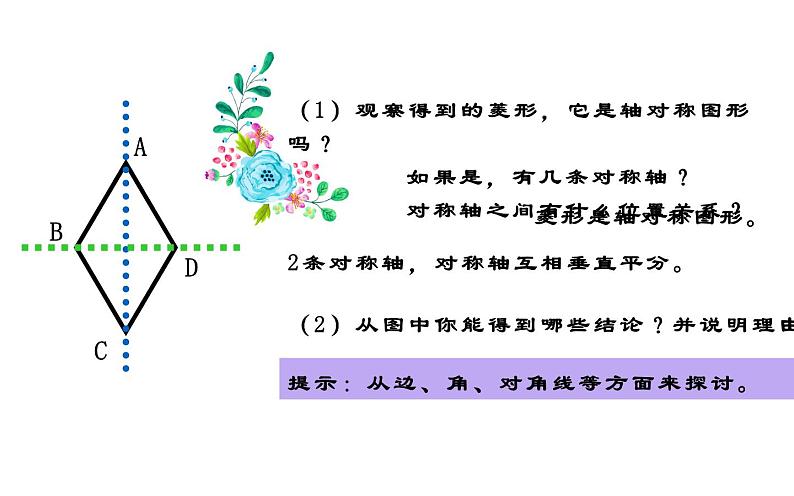
（2）从图中你能得到哪些结论？并说明理由。
提示：从边、角、对角线等方面来探讨。
（1）观察得到的菱形，它是轴对称图形吗？ 如果是，有几条对称轴？ 对称轴之间有什么位置关系？
2条对称轴，对称轴互相垂直平分。
由于平行四边形的对边相等，而菱形的邻边相等，故：
菱形的性质2：菱形的两条对角线互相垂直，并且每一条对角线平分一组对角。
菱形是特殊的平行四边形，具有平行四边形的所有性质。
菱形的性质1：菱形的四条边都相等。
符号语言∵四边形ABCD是菱形∴AB=BC=CD=AD
符号语言∵四边形ABCD是菱形∴AC⊥BDAC平分∠BAD和∠BCD； BD平分∠ABC和∠ADC
菱形的两条对角线互相平分
菱形的两组对边平行且相等
菱形的两组对角分别相等
菱形的两条对角线互相垂直平分，并且每一条对角线平分一组对角。
我们在学习平行四边形的判定和矩形的判定时，我们首先想到的第一种方法是什么？那么类比着它们，菱形的第一种判定方法是什么？
根据定义得：一组邻边相等的平行四边形是菱形。
命题：有四条边相等的四边形是菱形。
已知：在四边形ABCD中，AB=BC=CD=DA。求证：四边形ABCD是菱形
∵AB=CD，AD=BC
∴四边形ABCD是平行四边形
∴四边形ABCD是菱形
四条边都相等的四边形是菱形。
AB=BC=CD=DA
∵AB=BC=CD=DA
用一长一短两根细木条，在它们的中点处固定一个小钉，做成一个可以转动的十字，四周围上一根橡皮筋，做成一个四边形。转动木条，这个四边形什么时候变成菱形？
猜想：对角线互相垂直的平行四边形是菱形。
命题：对角线互相垂直的平行四边形是菱形。
∵四边形ABCD是平行四边形
∴平行四边形ABCD是菱形
求证：平行四边形ABCD是菱形。
已知：在平行四边形ABCD中，AC⊥BD。
对角线互相垂直的平行四边形是菱形。
∵在□ABCD中，AC⊥BD
有一组邻边相等的平行四边形叫做菱形。
有四条边相等的四边形是菱形。
下列三个图形都是菱形，正确吗？为什么？
有同学是这样做的：将一张长方形的纸对折、再对折，然后沿图中的虚线剪下，打开即可。你知道其中的道理吗？
如何利用折纸、剪切的方法，既快又准确地剪出一个菱形的纸片？