数学八年级下册18.2.1 矩形教学课件ppt

这是一份数学八年级下册18.2.1 矩形教学课件ppt，共19页。PPT课件主要包含了知识讲解，课堂练习，矩形的性质，归纳总结，你能证明吗，证一证，练一练，典例精析，试给出数学证明，∴ACBD等内容，欢迎下载使用。
目录 CONTENTS
1.理解矩形的概念，知道矩形与平行四边形的区别与 联系.（重点）2.会证明矩形的性质，会用矩形的性质解决简单的问 题.（重点、难点）3.掌握直角三角形斜边中线的性质，并会简单的运用. （重点）
观察下面图形,长方形在生活中无处不在.
你还能举出其他的例子吗？
思考 长方形跟我们前面学习的平行四边形有什么关系？
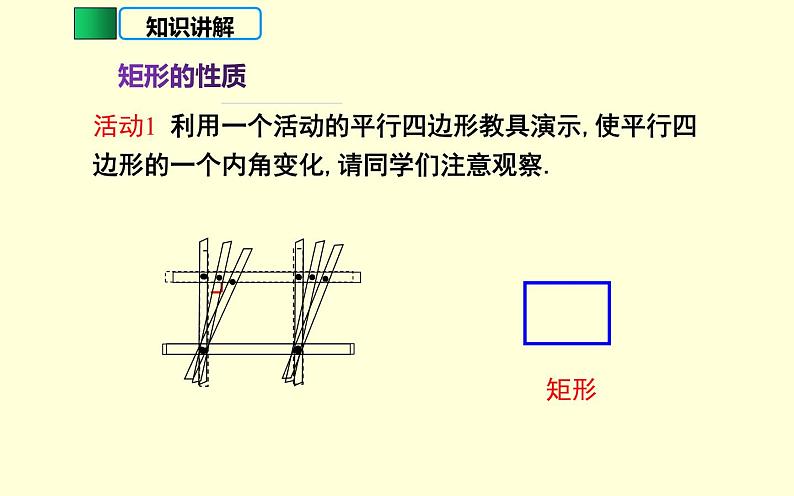
活动1 利用一个活动的平行四边形教具演示,使平行四边形的一个内角变化,请同学们注意观察.
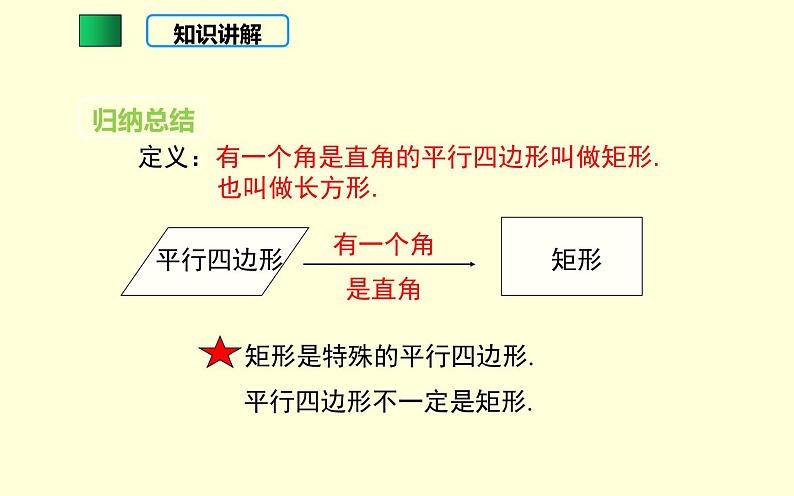
定义：有一个角是直角的平行四边形叫做矩形. 也叫做长方形.
平行四边形不一定是矩形.
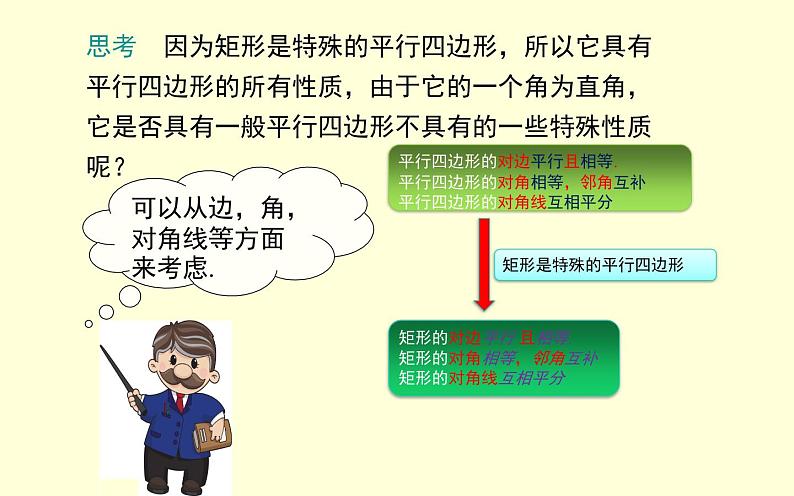
思考 因为矩形是特殊的平行四边形，所以它具有平行四边形的所有性质，由于它的一个角为直角，它是否具有一般平行四边形不具有的一些特殊性质呢？
可以从边，角，对角线等方面来考虑.
平行四边形的对边平行且相等.平行四边形的对角相等，邻角互补平行四边形的对角线互相平分
矩形的对边平行 且相等.矩形的对角相等，邻角互补矩形的对角线互相平分
矩形是特殊的平行四边形
活动：准备素材：直尺、量角器、（1）请同学们以小组为单位,测量课本第53页图18.2-3矩形ABCD的四个角与对角线的长度,并记录测量结果.
（P53 图18.2-3）
（2）根据测量的结果,你有什么猜想？
猜想1 矩形的四个角都是直角.
猜想2 矩形的对角线相等.
证明：∵四边形ABCD是矩形, ∴∠B=∠D,∠C=∠A, AB∥DC. ∴∠B+∠C=180°. 又∵∠B = 90°, ∴∠C = 90°. ∴∠B=∠C=∠D=∠A =90°.
已知：如图，四边形ABCD是矩形,∠B=90°.求证： ∠B=∠C=∠D=∠A=90°.
证明：∵四边形ABCD是矩形,∴AB=DC,∠ABC=∠DCB=90°,在△ABC和△DCB中,∵AB=DC,∠ABC=∠DCB,BC= CB,∴△ABC≌△DCB(SAS).∴AC=DB.
已知：如图，四边形ABCD是矩形,∠ABC=90°,对角线AC与DB相交于点O.求证：AC=DB.
矩形除了具有平行四边形所有性质，还具有的性质有：矩形的四个角都是直角.矩形的对角线相等.
几何语言描述：在矩形ABCD中，对角线AC与DB相交于点O.∠ABC=∠BCD=∠CDA=∠DAB =90°，AC=DB.
矩形的一条对角线能把矩形分成两个全等的直角三角形矩形的两条对角线能把矩形的分成四个等腰三角形
1.矩形 （填“是”或“不是”）轴对称图形，它有 条对称轴.
2.矩形具有而一般平行四边形不具有的性质是 ( ) A.对角线相等 B.对边相等 C.对角相等 D.对角线互相平分
例1 如图,在矩形ABCD中,两条对角线AC,BD相交于点O,∠AOB=60°,AB=4 ,求矩形对角线的长.
解：∵四边形ABCD是矩形. ∴AC = BD（矩形的性质）， OA= OC= AC,OB = OD = BD ,∴OA = OB.（等式的性质） 又∵∠AOB=60°, ∴△OAB是等边三角形， ∴OA=AB=4， ∴AC=BD=2OA=8.
矩形的对角线相等且互相平分
活动：如图，一张矩形纸片，并在上面画出两条对角线，沿着对角线AC剪去一半.
问题 Rt△ABC中，BO是一条怎样的线段？它的长度与斜边AC有什么关系？
猜想：直角三角形斜边上的中线等于斜边的一半.
证明: 延长BO至D, 使OD=BO, 连接AD、DC.
∵AO=OC, BO=OD，∴四边形ABCD是平行四边形.
∵∠ABC=90°,
∴平行四边形ABCD是矩形，
已知：如图，在Rt△ABC中，∠ABC=90°，BO是AC上的中线.求证: BO = AC .
1. 直角三角形斜边上的中线等于斜边的一半.
1.如图，在△ABC中,∠ABC = 90°,BD是斜边AC上的中线.(1)若BD=3cm,则AC =_____cm;(2)若∠C = 30° ,AB = 5cm,则AC =_____cm, BD = _____cm.
如图,在矩形ABCD中,两条对角线AC,BD相交于点O,若AB=AO, ,求∠ABD的度数
∵四边形ABCD是矩形.
OA= OC= AC, OB = OD = BD ,∴OA = OB.
∴△AOB是等边三角形，