初中数学18.1.1 平行四边形的性质教学课件ppt

这是一份初中数学18.1.1 平行四边形的性质教学课件ppt，共21页。PPT课件主要包含了新课引入，画一画，新课讲解，语言表述，归纳总结，说一说，猜一猜，量一量，做一做，证一证等内容，欢迎下载使用。

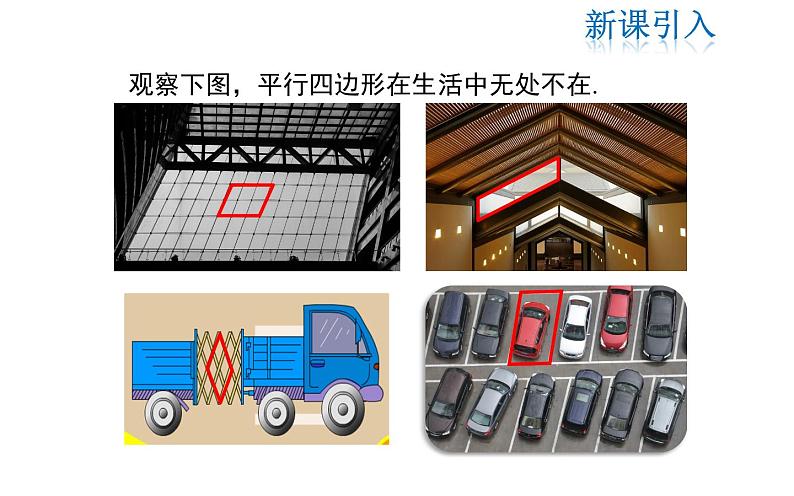
观察下图，平行四边形在生活中无处不在.
你还能举出其他的例子吗？
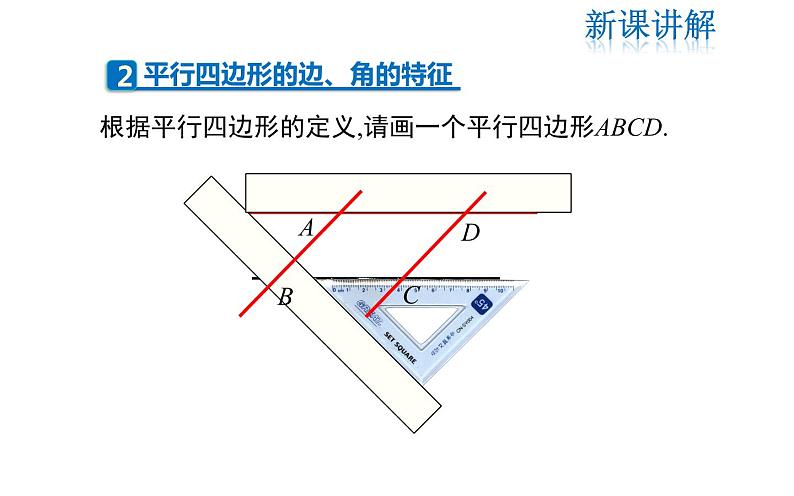
1.小学学过的平行四边形的定义2.用直尺、三角板画一个平行四边ABCD
根据平行四边形的定义,请画一个平行四边形ABCD.
平行四边形的边、角的特征
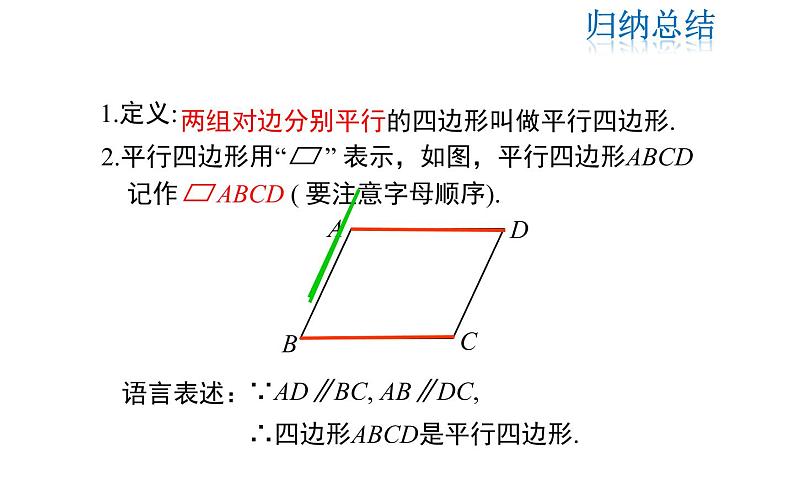
两组对边分别平行的四边形叫做平行四边形.
2.平行四边形用“ ” 表示，如图，平行四边形ABCD 记作 ABCD ( 要注意字母顺序).
∵AD∥BC, AB∥DC,∴四边形ABCD是平行四边形.
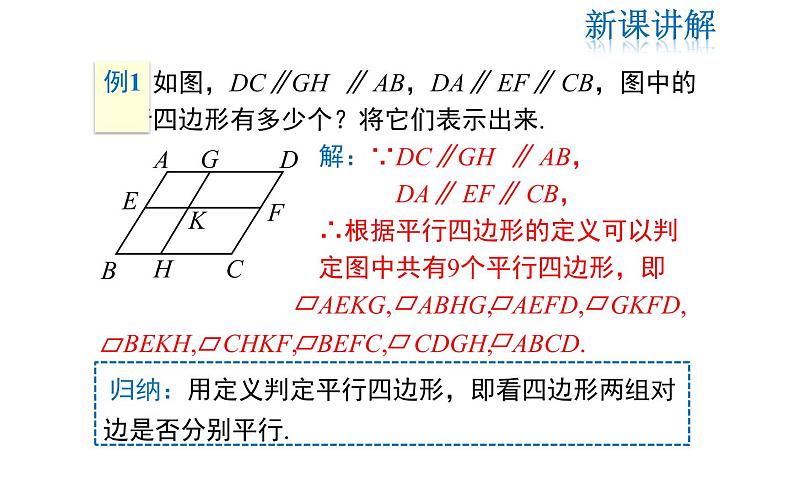
如图，DC∥GH ∥ AB，DA∥ EF∥ CB，图中的平行四边形有多少个？将它们表示出来.
解：∵DC∥GH ∥ AB， DA∥ EF∥ CB，∴根据平行四边形的定义可以判定图中共有9个平行四边形，即AEKG, ABHG, AEFD, GKFD,
BEKH, CHKF, BEFC, CDGH, ABCD.
归纳：用定义判定平行四边形，即看四边形两组对边是否分别平行.
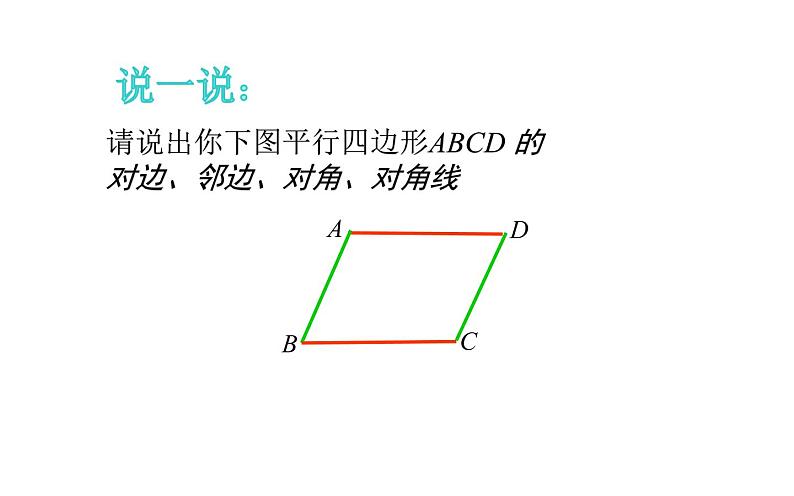
请说出你下图平行四边形ABCD 的对边、邻边、对角、对角线
下图平行四边形ABCD 的对边、对角之间分别有什么关系？
度量你所画的平行四边形的ABCD中个边的长度和各角的度数，是否和你的猜想一致？
将自制的一个平行四边形沿对角线剪开，把得到的两个三角形重合，观察原平行四边形的对边之间、对角之间是否仍有上述关系？
已知：四边形ABCD是平行四边形求证：(1) AD=BC AB=CD (2) ∠B=∠D ∠A=∠C
请你把得到的性质用数学符号表达出来
思考 不添加辅助线，你能否直接运用平行四边形的定义，证明其对角相等？
证明：∵四边形ABCD是平行四边形,∴AD∥BC，AB ∥ CD,∴∠A+∠B=180°，∠A+∠D=180°，∴∠B=∠D.同理可得，∠A=∠C.
平行四边形的对边相等．平行四边形的对角相等．
平行四边形的性质除了对边互相平行以外，还有:
如图，在 ABCD中.(1)若∠A =32。,求其余三个角的度数.
∵四边形ABCD是平行四边形，
且 ∠A =32。(已知),
∴ ∠A = ∠C=32。, ∠B= ∠D (平行四边形的对角相等).
又∵AD∥BC（平行四边形的对边平行）,
∴ ∠A + ∠B =180。(两直线平行，同旁内角互补),
∴ ∠B= ∠D= 180。- ∠A = 180。- 32。=148。.
(2)连结AC，已知 ABCD的周长等于20 cm，AC= 7cm，求△ABC的周长.
解：∵四边形ABCD是平行四边形(已知), ∴AB=CD，BC=AD(平行四边形的对边相等). 又∵AB+BC+CD+AD=20cm(已知), ∴AB+BC= 10cm. ∵AC=7cm, ∴ △ABC的周长为AB+BC+AC= 17cm.
【变式题】1.在 ABCD中,∠A:∠B=2:3,求各角的度数.
解： (1)∵∠A,∠B是平行四边形的两个邻角, ∴∠A+∠B=180°. 又∵∠A:∠B=2:3, ∴可设∠A=2x,∠B=3x, ∴2x+3x = 180°, 解得x = 36°. ∴ ∠A = ∠C=72°, ∠B= ∠D=108°.
平行四边形的邻角互补.
2.若 ABCD的周长为28cm, AB:BC=3:4,求各边的长度.
解： 在平行四边形ABCD中, AB=CD，BC=AD. ∵AB+BC+CD+AD=28cm, ∴AB+BC= 14cm. ∵AB:BC=3:4, ∴可设AB=3ycm,BC=4ycm, 则3y+4y=14，解得y=2. ∴AB=CD=6cm，BC=AD=8cm.
归纳：已知平行四边形的边角的比例关系求其他边角时，常会用到方程思想，结合平行四边形的性质列方程.
两组对边分别平行的四边形
两组对边分别平行，相等
两组对角分别相等，邻角互补