2021学年17.1 勾股定理教学ppt课件

这是一份2021学年17.1 勾股定理教学ppt课件，共17页。PPT课件主要包含了新课引入，一直角边2，另一直角边2，斜边2，∵S大正方形＝c2，赵爽弦图，b-a，毕达哥拉斯证法，a2+b2c2，勾股定理等内容，欢迎下载使用。

利用勾股定理解决简单的数学问题 .
我们一起穿越回到2500年前，跟随毕达哥拉斯再去他那位老朋友家做客，看到他朋友家用等腰三角形砖铺成的地面（如图）：
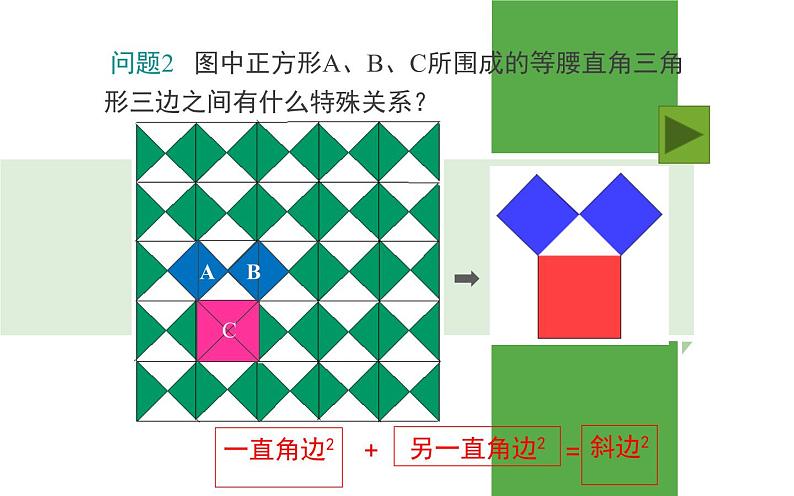
问题1 试问正方形A、B、C面积之间有什么样的数量关系？
问题2 图中正方形A、B、C所围成的等腰直角三角形三边之间有什么特殊关系？
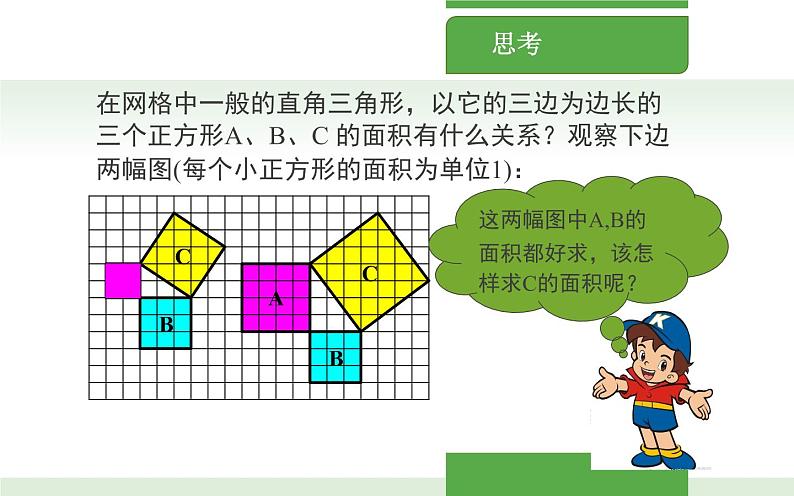
在网格中一般的直角三角形，以它的三边为边长的三个正方形A、B、C 的面积有什么关系？观察下边两幅图(每个小正方形的面积为单位1)：
这两幅图中A,B的面积都好求，该怎样求C的面积呢？
方法1：补形法(把以斜边为边长的正方形补成各边都在网格线上的正方形）：
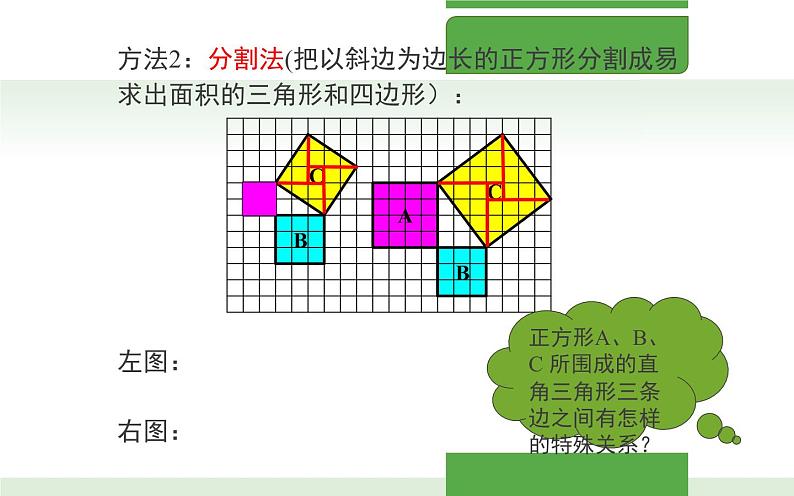
方法2：分割法(把以斜边为边长的正方形分割成易求出面积的三角形和四边形）：
正方形A、B、C 所围成的直角三角形三条边之间有怎样的特殊关系？
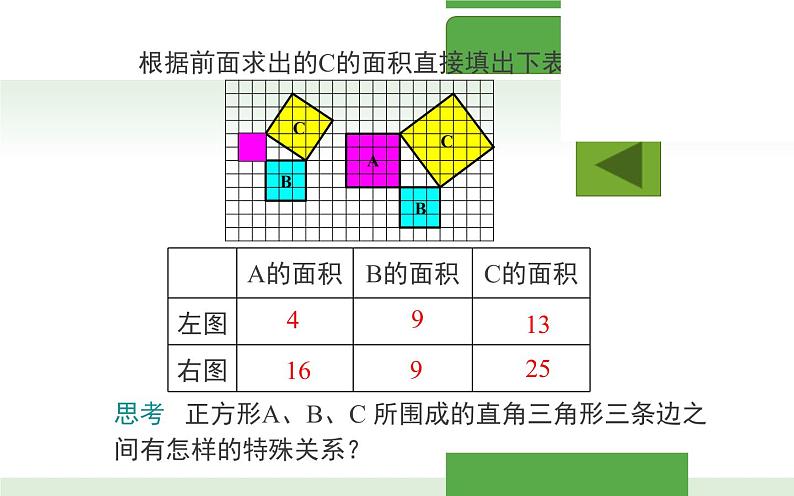
根据前面求出的C的面积直接填出下表：
思考 正方形A、B、C 所围成的直角三角形三条边之间有怎样的特殊关系？
拼一拼，请用四个全等的直角三角形纸片围出一个大正方形（允许中间有空隙），你能用不同的方式表示出大的正方形的面积吗？你还发现了什么？
S小正方形＝(b-a)2,
∴S大正方形＝4·S三角形＋S小正方形，
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智，它是我国古代数学的骄傲.因为，这个图案被选为2002年在北京召开的国际数学大会的会徽.
∴a2+b2+2ab=c2+2ab，
∴a2 +b2 =c2.
证明：∵S大正方形=(a+b)2=a2+b2+2ab,
如果直角三角形的两直角边长分别为a,b,斜边长为c，则
即直角三角形两直角边的平方和等于斜边的平方
1.在?ABC中，∠C=90°，BC=a，AC=b，AB=c。
(1)若a=1，b=2，求c
(2)若a=24，c=25，求b
已知直角三角形斜边和其中一条直角边长求另一条直角边时，可以利用平方差公式进行计算.
2.如图，从电线杆离地面６米处向地面拉一条长10米的缆绳，这条缆绳在地面的固定点距离电线杆底部为 米。
3.一个杆在离地面3m处折断，木杆顶部落在离木杆底端4m处。木杆折断之前有多高？
（1）若a：b=1：2 ，c=5,求a;
（2）若b=15，∠A=30°,求a,c.
4.在Rt△ABC中， ∠C=90°.
x2+(2x)2=52，
因此设a=x,c=2x,根据勾股定理建立方程得
(2x)2-x2=152，
已知直角三角形两边关系和第三边的长求未知两边时，要运用方程思想设未知数，根据勾股定理列方程求解.
5.在Rt△ABC中，AB＝4，AC＝3，求BC的长.
解：本题斜边不确定，需分类讨论：当AB为斜边时，如图，当BC为斜边时，如图，
当直角三角形中所给的两条边没有指明是斜边或直角边时，其中一较长边可能是直角边，也可能是斜边，这种情况下一定要进行分类讨论，否则容易丢解.