2020-2021学年18.2.3 正方形多媒体教学ppt课件

这是一份2020-2021学年18.2.3 正方形多媒体教学ppt课件，共19页。PPT课件主要包含了学习目标，正方形，写出证明过程，先判定菱形，先判定矩形，矩形条件2选1，菱形条件2选1，连接PC，∴∠FCE90°，∴PCEF等内容，欢迎下载使用。

探索并证明正方形的判定（重点）
会运用正方形的判定条件进行有关的论证和计算（难点）
了解平行四边形、矩形、菱形之间的联系和区别（难点）
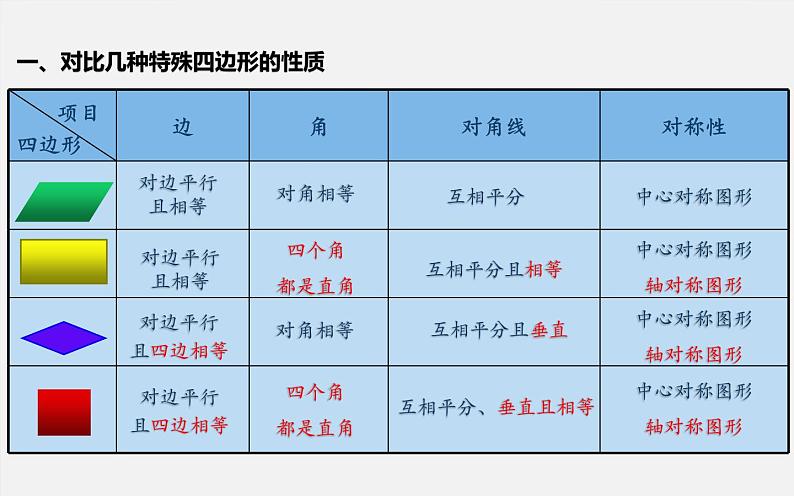
一、对比几种特殊四边形的性质
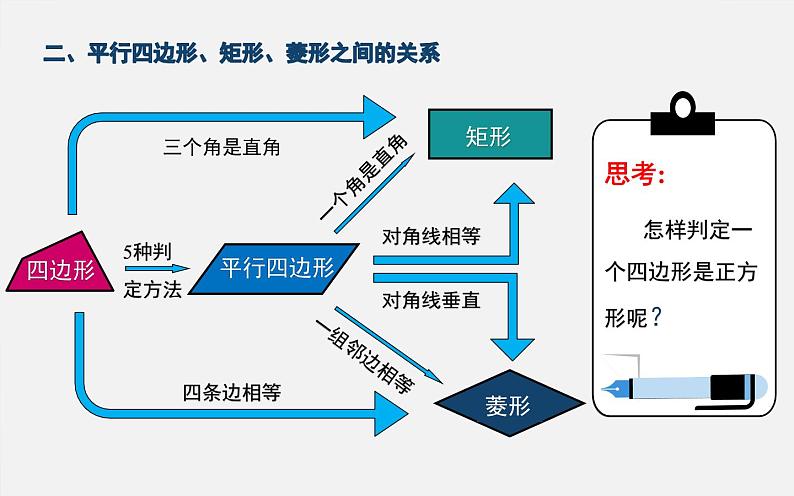
二、平行四边形、矩形、菱形之间的关系
思考: 怎样判定一个四边形是正方形呢？
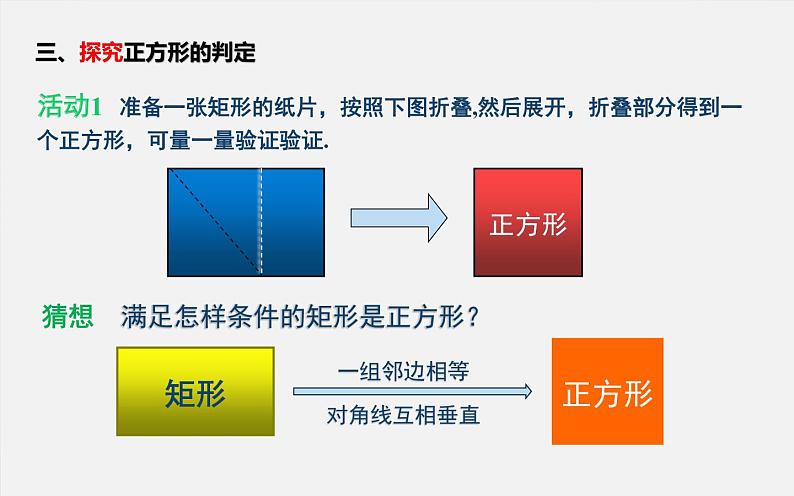
活动1 准备一张矩形的纸片，按照下图折叠,然后展开，折叠部分得到一个正方形，可量一量验证验证.
猜想 满足怎样条件的矩形是正方形？
已知：如图,在矩形ABCD中,AC , DB是它的两条对角线, AC⊥DB.求证：四边形ABCD是正方形.证明：∵ 四边形ABCD是矩形, ∴ AO=CO=BO=DO ，∠ADC=90°. ∵ AC⊥DB, ∴ AD=AB=BC=CD, ∴ 四边形ABCD是正方形.
对角线互相垂直的矩形是正方形.
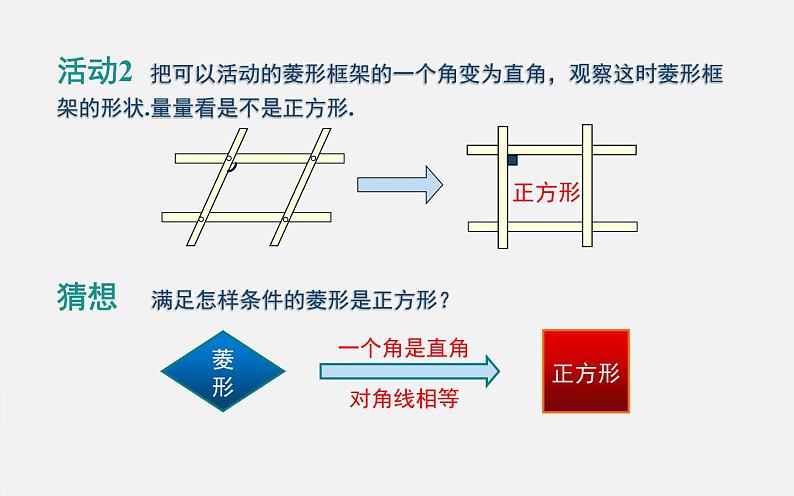
活动2 把可以活动的菱形框架的一个角变为直角，观察这时菱形框架的形状.量量看是不是正方形.
猜想 满足怎样条件的菱形是正方形？
已知：如图,在菱形ABCD中,AC , DB是它的两条对角线, AC=DB.求证：四边形ABCD是正方形.证明：∵ 四边形ABCD是菱形, ∴ AB=BC=CD=AD, AC⊥DB. ∵ AC=DB, ∴ AO=BO=CO=DO, ∴ △AOD,△AOB,△COD,△BOC是等腰直角三角形， ∴ ∠DAB=∠ABC=∠BCD=∠ADC=90°, ∴ 四边形ABCD是正方形.
对角线相等的菱形是正方形.
想一想：正方形判定有几条途径？
归纳：平行四边形、矩形、菱形、正方形之间的关系
例题 求证：正方形的两条对角线把这个正方形分成四个全等的等 腰直角三角形.
已知：如图，正方形ABCD中，对角线AC、BD相交于O。
证明：∵ 四边形ABCD是正方形。 ∴ AC＝BD，AC⊥BD， OA＝OB＝OC＝OD， ∴ △ABO，△BCO，△CDO， △DAO都是等腰直角三角形， 并△ABO≌△BCO≌△CDO≌△DAO.
求证：△ABO，△BCO，△CDO; △DAO是全等的等腰直角三角形。
1.下列命题正确的是（ ） A. 四个角都相等的四边形是正方形 B. 四条边都相等的四边形是正方形 C. 对角线相等的平行四边形是正方形 D. 对角线互相垂直的矩形是正方形
2. 如图，已知四边形ABCD是平行四边形，下列结论中不正确的是（ 　） A. 当AB=BC时，四边形ABCD是菱形 B．当AC⊥BD时，四边形ABCD是菱形 C．当∠ABC=90°时，四边形ABCD是矩形 D．当AC=BD时，四边形ABCD是正方形
3. 如图，四边形ABCD中，ABC=∠BCD=∠CDA=90°， 请添加一个条件____________________， 可得出该四边形是正方形．
AB=BC(答案不唯一)
4. 已知四边形ABCD是平行四边形，再从①AB=BC，②∠ABC=90°，③AC=BD， ④AC⊥BD四个条件中，选两个作为补充条件后，使得四边形ABCD是正方形， 其中错误的是_________________（只填写序号）．
1．如图在正方形ABCD中，对角线AC与BD相交于点O, 若O点移动至E点时，连接AE、CE，你有那些结论？
2. 如图所示，正方形ABCD中，P为BD上一点，PE⊥BC于E， PF⊥DC于F。试说明：AP=EF
∵ PE⊥BC ， PF⊥DC
而四边形ABCD是正方形
∴ 四边形PECF是矩形
又∵ 四边形BAPC是以BD为轴的轴对称图形
归纳：平行四边形、矩形、菱形 、正方形之间的关系
1. 本章学习了哪些四边形？是按照怎样的研究思 路进行的？2. 研究各种四边形时，我们的研究内容、研究步 骤、研究方法各是怎样的？
平行四边形——矩形、菱形——正方形，按由一般到特殊的思路研究的。
研究内容：边、角、对角线的特征研究步骤：下定义、探性质、研判定。研究方法： （1）把四边形的问题转化为三角形的问题。 （2）特殊平行四边形类比平行四边形研究。