人教版九年级下册26.1.1 反比例函数教课ppt课件

这是一份人教版九年级下册26.1.1 反比例函数教课ppt课件，共16页。PPT课件主要包含了xykk≠0，t100v，ykx-1，xyk，跟踪练习2，超越思维，反思小结等内容，欢迎下载使用。
[活动1]问题 y=kx （k≠0） y=kx+b （k≠0） y=2x y=3
1.回顾函数，正比例函数，一次函数等概念。
2.已知y 是x 的正比例函数,当x=3时,y=6(1)写出y与x的函数关系式
(2)当x=1.5时,求y的值.
[活动2]思考什么是反比例关系？ 2. 体育课上，测试百米成绩，那么时间t与 平均速度v之间的关系是怎么样的？你能 用含t代数式表示V吗？3. 你还能举出具有反比例关系的例子吗？
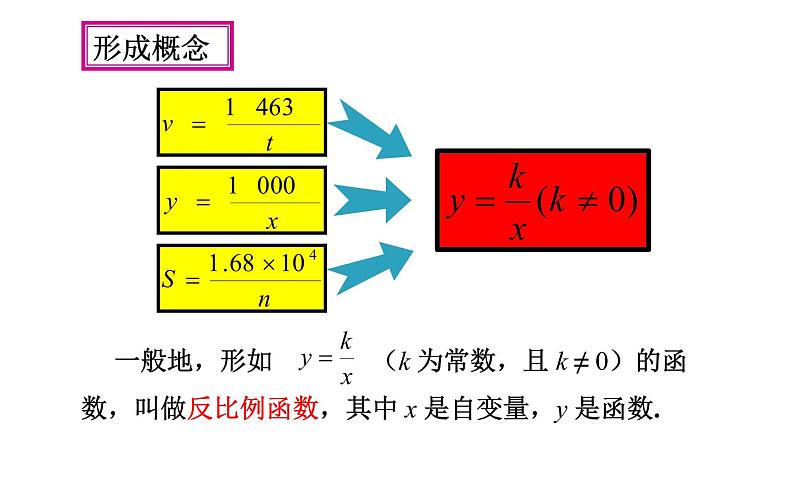
1、京沪铁路全程为1463km，某次列车的平均速度为v（km/h）随此次列车的全程运行时间t（h）的变化而变化。
2、某住宅小区要种植一个面积为1000m2的矩形草坪，草坪的长y(单位:m)随宽x (单位:m)的变化而变化。
下列问题中，变量间的对应关系可以用怎样的函数关系表示？这些函数有什么共同特点？
3、已知北京市的总面积为1.68×104平方千米，人均占有的土地面积s(单位:平方千米/人)随全市总人口n(单位:人)的变化而变化。
反比例函数的三种形式：
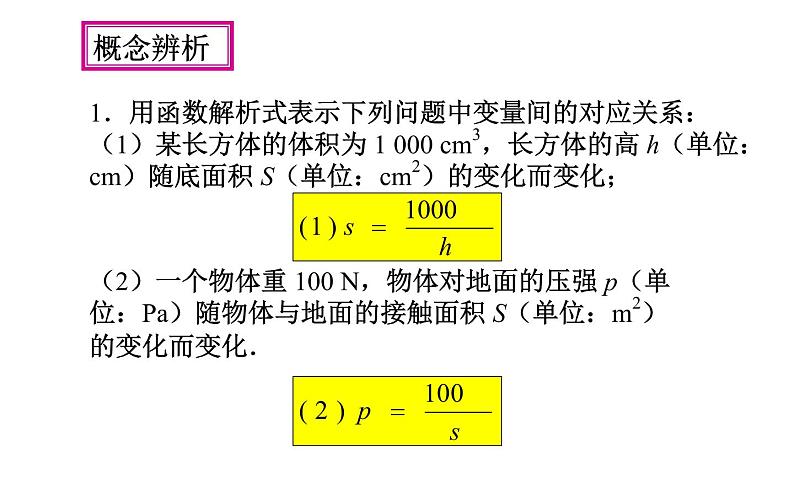
1．用函数解析式表示下列问题中变量间的对应关系：（1）某长方体的体积为 1 000 cm3，长方体的高 h（单位：cm）随底面积 S（单位：cm2）的变化而变化；
（2）一个物体重 100 N，物体对地面的压强 p（单位：Pa）随物体与地面的接触面积 S（单位：m2）的变化而变化．
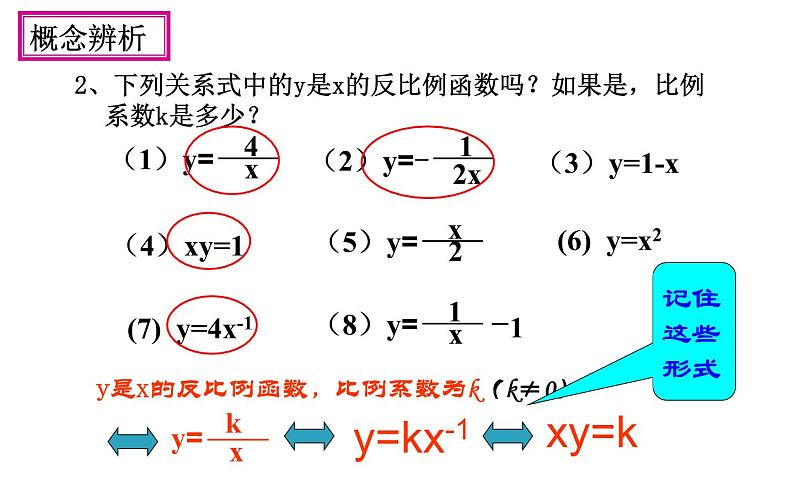
2、下列关系式中的y是x的反比例函数吗？如果是，比例系数k是多少？
y是x的反比例函数，比例系数为k（k≠0）
例1　已知 y 是 x 的反比例函数，并且当 x=2 时， y=6（1）写出 y 关于 x 的函数解析式；（2）当 x=4 时，求 y 的值.
2．已知 y 与 x2 成反比例，并且当 x=3 时，y=4．（1）写出 y 关于 x 的函数解析式；（2）当 x=1.5 时，求 y 的值；（3）当 y=6 时，求 x 的值.
已知函数y=（5m-3）x2-n +（n+m）当m,n 为何值时，该函数是一次函数？当m,n 为何值时，该函数是正比例函数？当m,n 为何值时，该函数是反比例函数？
解：（1）当函数y=（5m-3）x2-n +（n+m）是一次函数时，2-n=1，且5m-3≠0， 所以，n=1，m ≠3|5（2）当函数y=（5m-3）x2-n +（n+m）是正比例函数时，2-n=1 m+n=0 所以，n=1，m=-1 5m-3≠0（3）当函数y=（5m-3）x2-n +（n+m）是反比例函数时，2-n=-1， m+n=0 所以，n=3，m=-3 5m-3≠0
4、已知函数 y = y1 + y2，y1与x 成正比例，y2与x成反比例，且当x=1时，y=4；当x=2时，y=5。(1)求y与x的函数关系式；(2)当x=4时，y 的值。
方法：先分别设y1,y2与x的关系式，将两组值代入所设的函数关系式中，求出函数的值。
∵x=1时，y=4；x=2时，y=5，
y=kx-1 xy=k （ K≠0 ） 二、用待定系数法求函数解析式
一、反比例函数的意义：若　　　　　，则y是x的反比例函数。　　
通过本节课的学习，你对反比例函数有怎样的认识？