初中数学人教版九年级下册第二十七章 相似27.2 相似三角形27.2.1 相似三角形的判定课文配套课件ppt

这是一份初中数学人教版九年级下册第二十七章 相似27.2 相似三角形27.2.1 相似三角形的判定课文配套课件ppt，共16页。PPT课件主要包含了思考如何证明，∴△ADE≌△，∵∠A∠A’，∠A∠A’，判定SAS，例题讲解等内容，欢迎下载使用。
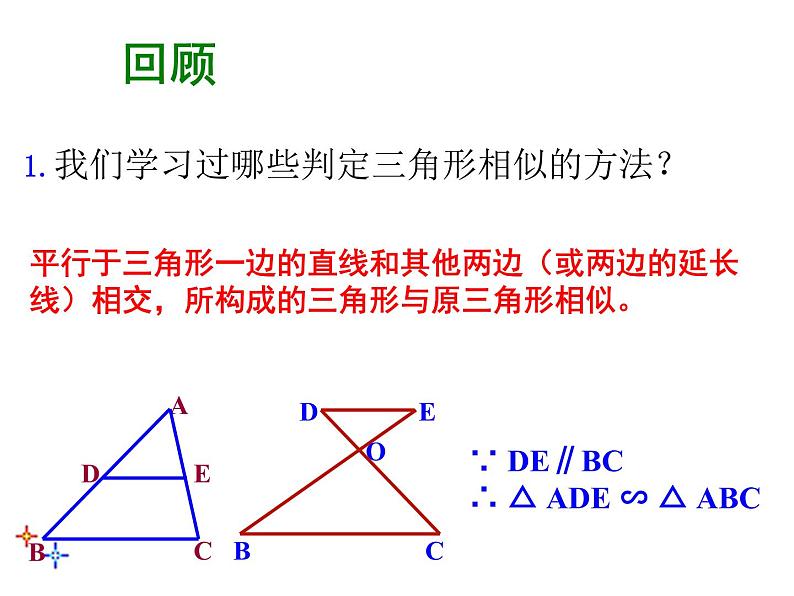
1.我们学习过哪些判定三角形相似的方法？
∵ DE∥BC ∴ △ ADE ∽ △ ABC
平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似。
2．全等三角形与相似三角形有怎样的关系？
3．如果要判定△ABC与△A′B′C′相似，是不是一定需要一一验证所有的对应角和对应边的关系？
由三角形全等的SSS判定方法，我们会想如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么能否判定这两个三角形相似呢？
探究1：任意画一个三角形，再画一个三角形，使它的各边长都是原来三角形各边长的k倍，度量这两个三角形的对应角，它们相等吗？这两个三角形相似吗？与同学交流一下，看看是否有同样的结论．学生动手画图、测量，独立研究后再小组讨论．三角形相似的判定方法SSS：三边成比例的两个三角形相似．
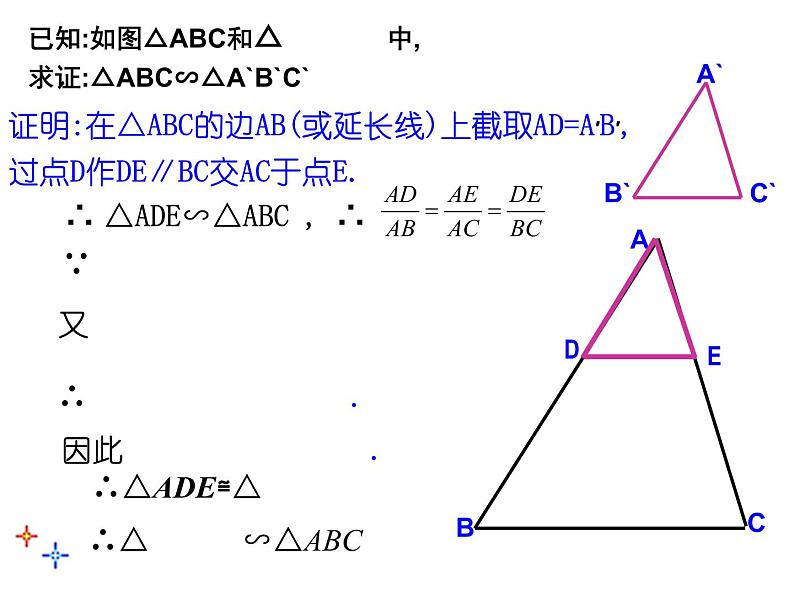
已知:如图△ABC和△ 中, 求证:△ABC∽△A`B`C`
证明:在△ABC的边AB(或延长线)上截取AD=A′B′,
过点D作DE∥BC交AC于点E.
∴ △ADE∽△ABC , ∴
∴ .
因此 .
∴△ ∽△ABC
△ABC∽△A’B’C’
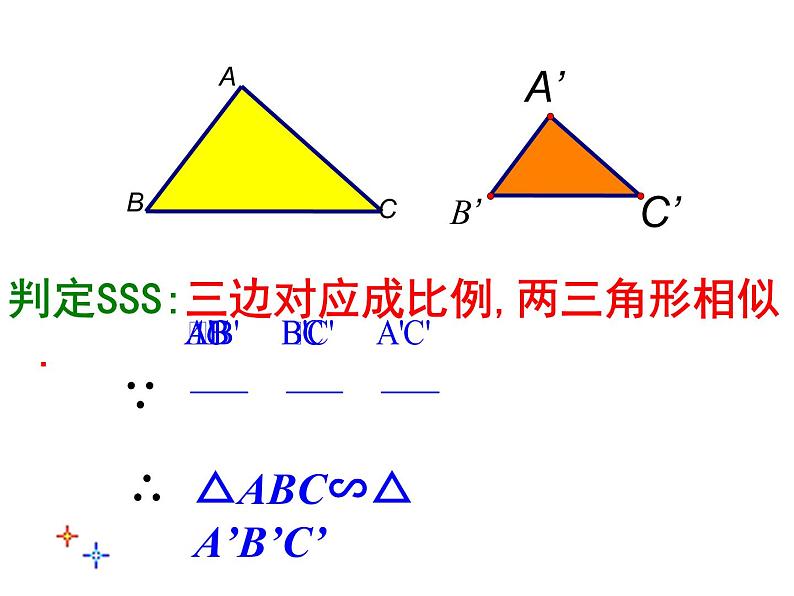
判定SSS:三边对应成比例,两三角形相似.
探究2：利用刻度尺和量角器画△ABC和△A′B′C′，使∠A＝∠A′，和都等于给定的值k，量出它们的第三组对应边BC和B′C′的长，它们的比等于k吗？另外两组对应角∠B与∠B′，∠C与∠C′是否相等？改变∠A或k值的大小，再试一试，是否有同样的结论？学生动手画图、测量，独立研究．三角形相似的判定方法SAS：两边成比例且夹角相等的两个三角形相似．
如图,在△ABC和△A’B’C’中,
求证:△ABC∽△A’B’C’
证明:在线段A’B’(或它的延长线)上截取A’D=AB,过点D作DE//B’C’,交A’C’于点E,
∴△A’DE∽△A’B’C’
∴△A’DE≌△ABC
∴△ABC∽△A’B’C’
两边对应成比例且夹角相等，两三角形相似。
在△ABC和△A’B’C’中,
例1 根据下列条件，判断△ABC和△A′B′C′是否相似，并说明理由．(1)∠A＝40°，AB＝8 cm，AC＝15 cm，∠A′＝40°，A′B′＝16 cm，A′C′＝30 cm；(2)AB＝10 cm，BC＝8 cm，AC＝16 cm，A′B′＝20 cm，B′C′＝16 cm，A′C′＝32 cm.
例2.如图，在△ABC中，D在AC上，已知AD=2 cm，AB=4cm，AC=8cm，
求证：△ABD∽△ABC.
例 3. 如图矩形ABCD是由三个正方形ABEG,GEFH,HFCD组成的,找出图中的相似三角形.
解:△ AEF∽ △CEA.理由是:设小正方形的边长是1,由勾股定理得
∵∠ AEF = ∠CEA=135°.
∴△ AEF ∽ △CEA.
课堂练习（1）如图，AB⊥BC，DC⊥BC，AB=8，DC=6，BC=14，在BC上是找出点P使△ABP与△DCP相似。
∴ΔABC∽ΔADE∴∠BAC=∠DAE∴∠BAC━∠DAC=∠DAE━∠DAC即∠BAD=∠CAE
（2）.如图已知, = = 试说明：∠BAD=∠CAE.
4:2=5:x=6:y4:x=5:2=6:y4:x=5:y=6:2
3：要作两个形状相同的三角形框架,其中一个三角形的三边的长分别为4、5、6,另一个三角形框架的一边长为2,怎样选料可使这两个三角形相似?