

高考数学真题专项练习 专题30 排列组合、二项式定理【理】(解析版)
展开专题30 排列组合、二项式定理【理】
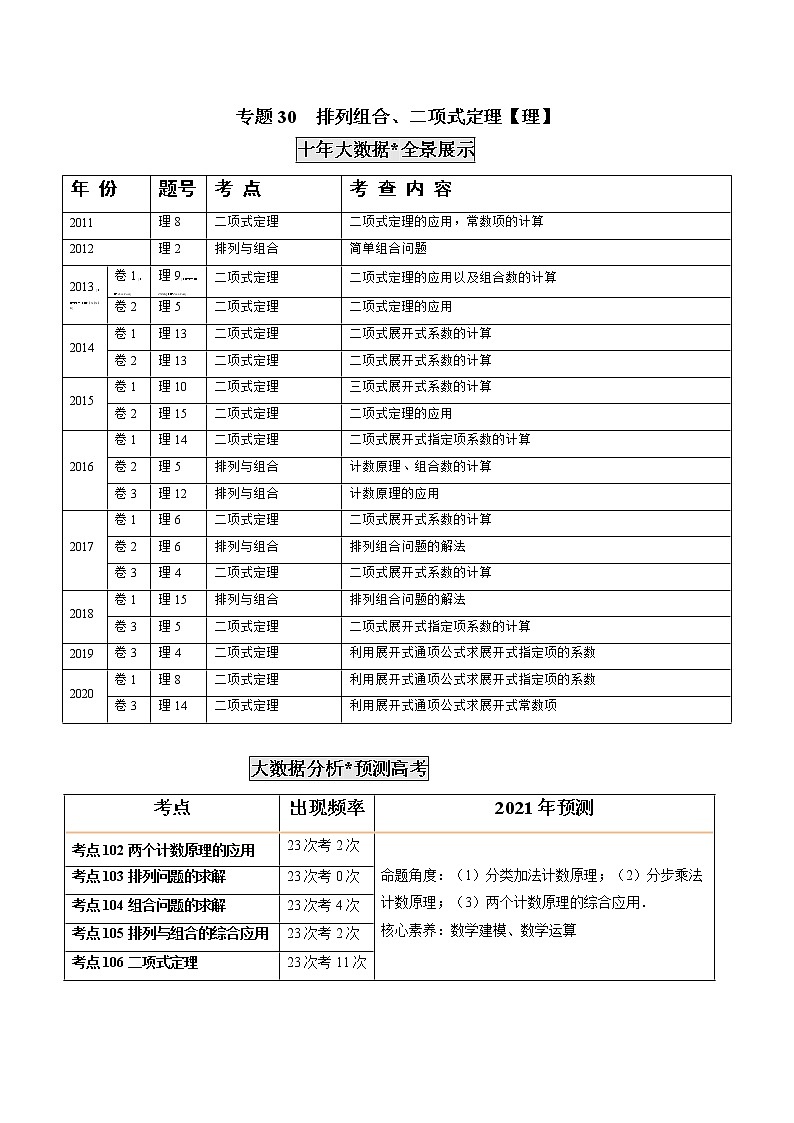
十年大数据*全景展示
年 份
题号
考 点
考 查 内 容
2011
理8
二项式定理
二项式定理的应用,常数项的计算
2012
理2
排列与组合
简单组合问题
2013[来源:学§科§网Z§X§X§K]
卷1[来源:Zxxk.Com]
理9[来源:学科网ZXXK][来源:Zxxk.Com]
二项式定理
二项式定理的应用以及组合数的计算
卷2
理5
二项式定理
二项式定理的应用
2014
卷1
理13
二项式定理
二项式展开式系数的计算
卷2
理13
二项式定理
二项式展开式系数的计算
2015
卷1
理10
二项式定理
三项式展开式系数的计算
卷2
理15
二项式定理
二项式定理的应用
2016
卷1
理14
二项式定理
二项式展开式指定项系数的计算
卷2
理5
排列与组合
计数原理、组合数的计算
卷3
理12
排列与组合
计数原理的应用
2017
卷1
理6
二项式定理
二项式展开式系数的计算
卷2
理6
排列与组合
排列组合问题的解法
卷3
理4
二项式定理
二项式展开式系数的计算
2018
卷1
理15
排列与组合
排列组合问题的解法
卷3
理5
二项式定理
二项式展开式指定项系数的计算
2019
卷3
理4
二项式定理
利用展开式通项公式求展开式指定项的系数
2020
卷1
理8
二项式定理
利用展开式通项公式求展开式指定项的系数
卷3
理14
二项式定理
利用展开式通项公式求展开式常数项
大数据分析*预测高考
考点
出现频率
2021年预测
考点102两个计数原理的应用
23次考2次
命题角度:(1)分类加法计数原理;(2)分步乘法计数原理;(3)两个计数原理的综合应用.
核心素养:数学建模、数学运算
考点103排列问题的求解
23次考0次
考点104组合问题的求解
23次考4次
考点105排列与组合的综合应用
23次考2次
考点106二项式定理
23次考11次
十年试题分类*探求规律
考点102 两个计数原理的应用
1.(2016全国II理)如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为
A.24 B.18 C.12 D.9
【答案】B【解析】由题意可知有6种走法,有3种走法,由乘法计数原理知,共有 种走法,故选B.
2.(2014新课标理1理)4位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率为
A. B. C. D.
【答案】D【解析】.
3.(2012湖北理)回文数是指从左到右读与从右到左读都一样的正整数.如22,121,3443,94249等.显然2位回文数有9个:11,22,33,…,99.3位回文数有90个:101,111,121,…,191,202,…,999.则
(Ⅰ)4位回文数有 个;
(Ⅱ)位回文数有 个.
【解析】(Ⅰ)4位回文数只用排列前面两位数字,后面数字就可以确定,但是第一位不能为0,有9(1~9)种情况,第二位有10(0~9)种情况,所以4位回文数有种.答案:90
(Ⅱ)解法一:由上面多组数据研究发现,位回文数和位回文数的个数相同,所以可以算出位回文数的个数.位回文数只用看前位的排列情况,第一位不能为0有9种情况,后面项每项有10种情况,所以个数为.
解法二:可以看出2位数有9个回文数,3位数90个回文数。计算四位数的回文数是可以看出在2位数的中间添加成对的“00,11,22,……99”,因此四位数的回文数有90个按此规律推导,而当奇数位时,可以看成在偶数位的最中间添加0~9这十个数,因此,则答案为.
4.(2011湖北理)给个自上而下相连的正方形着黑色或白色.当时,在所有不同的着色方案中,黑色正方形互不相邻的着色方案如下图所示:
由此推断,当时,黑色正方形互不相邻的着色方案共有 种,至少有两个黑色正方形相邻的着色方案共有 种,(结果用数值表示)
【解析】(Ⅰ)4位回文数只用排列前面两位数字,后面数字就可以确定,但是第一位不能为0,有9(1~9)种情况,第二位有10(0~9)种情况,所以4位回文数有种.答案:90
(Ⅱ)法一、由上面多组数据研究发现,位回文数和位回文数的个数相同,所以可以算出位回文数的个数.位回文数只用看前位的排列情况,第一位不能为0有9种情况,后面项每项有10种情况,所以个数为.
法二、可以看出2位数有9个回文数,3位数90个回文数.计算四位数的回文数是可以看出在2位数的中间添加成对的“00,11,22,……99”,因此四位数的回文数有90个按此规律推导,而当奇数位时,可以看成在偶数位的最中间添加0~9这十个数,因此,则答案为.
考点103 排列问题的求解
5.(2016四川理)用数字1,2,3,4,5组成没有重复数字的五位数,其中奇数的个数为
A.24 B.48 C.60 D.72
【答案】D【解析】由题意,要组成没有重复的五位奇数,则个位数应该为1、3、5中任选一个,有 种方法,其他数位上的数可以从剩下的4个数字中任选,进行全排列,有种方法,所以其中奇数的个数为,故选D.
6.(2015四川理)用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40000大的偶数共有
A.144个 B.120个 C.96个 D.72个
【答案】B【解析】据题意,万位上只能排4、5.若万位上排4,则有个;若万位上排5,则有个.所以共有个,故选B.
7.(2015广东理)某高三毕业班有人,同学之间两两彼此给对方仅写一条毕业留言,那么全班共写了 条毕业留言.(用数字作答)
【答案】1560 【解析】由题意,故全班共写了1560条毕业留言.
8.(2014北京理)把5件不同产品摆成一排,若产品与产品相邻,且产品与产品不相邻,则不同的摆法有_______种.
【答案】36【解析】将A、B捆绑在一起,有种摆法,再将它们与其他3件产品全排列,有种摆法,共有=48种摆法,而A、B、C 3件在一起,且A、B相邻,A、C相邻有CAB、BAC两种情况,将这3件与剩下2件全排列,有种摆法,故A、B相邻,A、C不相邻的摆法由48-12=36.
9.(2013北京理)将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少一张,如果分给同一人的两张参观券连号,那么不同的分法种数是 .
【答案】96【解析】5张参观券分成4堆,有2个联号有4种分法,每种分法分给4个人有种方法,∴总共有.
10.(2013浙江理)将六个字母排成一排,且均在的同侧,则不同的排法共有________种(用数字作答).
【答案】480【解析】第一类,字母C排在左边第一个位置,有种;第二类,字母C排在左边第二个位置,有种;第三类,字母C排在左边第三个位置,有种,由对称性可知共有2´(++)=480种.
考点104 组合问题的求解
11.【2020山东卷3】6名同学到甲、乙、丙三个场馆做志愿者,每名同学只去个场馆,甲场馆安排名,乙场馆安排名,丙场馆安排名,则不同的安排方法共有 ( )
A.种 B.种 C.种 D.种
【答案】C
【思路导引】利用分步计算原理,结合组合数的计算,计算出不同的安排方法.
【解析】首先从名同学中选名去甲场馆,方法数有;然后从其余名同学中选名去乙场馆,方法数有;最后剩下的名同学去并场馆,故不同的安排方法共有种,故选C.
12.(2018全国Ⅱ理)我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是
A. B. C. D.
【答案】C【解析】不超过30的素数有2,3,5,7,11,13,17,19,23,29,共10个,从中随机选取两个不同的数有种不同的取法,这10个数中两个不同的数的和等于30的有3对,所以所求概率,故选C.
13.(2017山东理)从分别标有,,,的张卡片中不放回地随机抽取2次,每次抽取1张.则抽到的2张卡片上的数奇偶性不同的概率是
A. B. C. D.
【答案】C【解析】不放回的抽取2次有,如图
可知与是不同,所以抽到的2张卡片上的数奇偶性不同有=40,所求概率为.
14.(2014广东理)设集合,那么集合A中满足条件“”的元素个数为( )
A.60 B.90 C.120 D.130
【答案】D【解析】易知1或2或3,下面分三种情况讨论.其一:1,此时,从中任取一个让其等于1或-1,其余等于0,于是有种情况;其二:2,此时,从中任取两个让其都等于1或都等于-1或一个等于1、另一个等于-1,其余等于0,于是有种情况;其三:3,此时,从中任取三个让其都等于1或都等于-1或两个等于1、另一个等于-1或两个等于-1、另一个等于1,其余等于0,于是有种情况.由于.
15.(2014安徽理)从正方体六个面的对角线中任取两条作为一对,其中所成的角为的共有
A.24对 B.30对 C.48对 D.60对
【答案】C【解析】解法一(直接法):如图,在上底面中选,四个侧面中的面对角线都与它成,共8对,同样对应的也有8对,下底面也有16对,这共有32对;左右侧面与前后侧面中共有16对,所以全部共有48对.
解法二(间接法):正方体的12条面对角线中,任意两条垂直、平行或成角为,所以成角为的共有.
16.(2013山东理)用0,1,…,9十个数学,可以组成有重复数字的三位数的个数为
A.243 B.252 C.261 D.279
【答案】B【解析】能够组成三位数的个数是9×10×10=900,能够组成无重复数字的三位数的个数是9×9×8 =648.故能够组成有重复数字的三位数的个数为.
17.(2012新课标理)将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有
A.12种 B.10种 C.9种 D.8种
【答案】A【解析】先安排1名教师和2名学生到甲地,再将剩下的1名教师和2名学生安排到乙地,共有种.
18.(2012浙江理)若从1,2,3,…,9这9个整数中同时取4个不同的数,其和为偶数,则不同的取法共有
A.60种 B.63种 C.65种 D.66种
【答案】D【解析】和为偶数,则4个数都是偶数,都是奇数或者两个奇数两个偶数,则有种取法.
19.(2012山东理)现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张,从中任取3张,要求这3张卡片不能是同一种颜色,并且红色卡片至多1张,不同取法的种数是
A.232 B.252 C.472 D.484
【答案】C【解析】若没有红色卡片,则需从黄、蓝、绿三色卡片中选3张,若都不同色则有=64,若2张同色,则有,若红色1张,其余2张不同色,则有,其余2张同色则有,所以共有64+144+192+72=472.
另解1:,答案应选C.
另解2:.
20.【2020上海卷9】从6个人选4个人去值班,每人值班一天,第一天安排1个人,第二天安排1个人,第三天安排2个人,则共有 种安排情况.
【答案】180
【解析】按照先选再排的方法可知共有种方法.
故答案为:180
21.(2018全国Ⅰ理)从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有 种.(用数字填写答案)
【答案】16【解析】通解 可分两种情况:第一种情况,只有1位女生入选,不同的选法有
(种);第二种情况,有2位女生入选,不同的选法有(种).
根据分类加法计数原理知,至少有l位女生人选的不同的选法有16种.
优解 从6人中任选3人,不同的选法有(种),从6人中任选3人都是男生,不同的选法有(种),所以至少有1位女生入选的不同的选法有20–4 =16(种).
22.(2014广东理)从0,1,2,3,4,5,6,7,8,9中任取七个不同的数,则这七个数的中位数是6的概率为 .
【答案】【解析】6之前6个数中取3个,6之后3个数中取3个,.
23.(2014江西理)10件产品中有7件正品、3件次品,从中任取4件,则恰好取到1件次品的概率是________.
【答案】【解析】从10件产品中任取4件共有=210种不同取法,因为10件产品中有7件正品、3件次品,所以从中任取4件恰好取到1件次品共有种不同的取法,故所求的概率为.
24.(2013新课标2理)从个正整数1,2,…,中任意取出两个不同的数,若取出的两数之和等于5的概率为,则=________.
【答案】8【解析】由题意,解得.
25.(2011湖北理)给个自上而下相连的正方形着黑色或白色.当时,在所有不同的着色方案中,黑色正方形互不相邻的着色方案如下图所示:
由此推断,当时,黑色正方形互不相邻的着色方案共有 种,至少有两个黑色正方形相邻的着色方案共有 种,(结果用数值表示)
【答案】21 43【解析】时,黑色正方形互不相邻的着色方案种数分别为2,3,5,8,由此可看出后一个总是前2项之和,故时应为5+8=13,时应为8+13=21;时,所有的着色方案种数为种,∴至少有两个黑色正方形相邻的着色方案共有种.
考点105 排列与组合的综合应用
26.【2020全国Ⅱ理14】4名同学到3个小区参加垃圾分类宣传活动,每名同学只去1个小区,每个小区至少安排1名同学,则不同的安排方法共有______种. .
【答案】
【解析】4名同学到3个小区参加垃圾分类宣传活动,每名同学只去1个小区,每个小区至少安排1名同学,先取2名同学看作一组,选法有:,现在可看成是3组同学分配到3个小区,分法有:,根据分步乘法原理,可得不同的安排方法种,故答案为:.
27.(2017新课标理Ⅱ理)安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有
A.12种 B.18种 C.24种 D.36种
【答案】D【解析】由题意可得,一人完成两项工作,其余两人每人完成一项工作,据此可得,只要把工作分成三份:有种方法,然后进行全排列,由乘法原理,不同的安排方式共有种.故选D.
28.(2018浙江理)从1,3,5,7,9中任取2个数字,从0,2,4,6中任取2个数字,一共可以组成 个没有重复数字的四位数.(用数字作答)
【答案】1260【解析】若取的4个数字不包括0,则可以组成的四位数的个数为;若取的4个数字包括0,则可以组成的四位数的个数为.综上,一共可以组成的没有重复数字的四位数的个数为+ =720+ 540 =1 260.
29.(2017浙江理)从6男2女共8名学生中选出队长1人,副队长1人,普通队员2人组成4人服务队,要求服务队中至少有1名女生,共有 种不同的选法.(用数字作答)
【答案】660【解析】分两步,第一步,选出4人,由于至少1名女生,故有种不同的选法;第二步,从4人中选出队长、副队长各一人,有种不同的选法,根据分步乘法计数原理共有种不同的选法.
30.(2017天津理)用数字1,2,3,4,5,6,7,8,9组成没有重复数字,且至多有一个数字是偶数的四位数,这样的四位数一共有___________个.(用数字作答)
【答案】1080【解析】分两种情况,只有一个数字为偶数有个,没有偶数有个,所以共有个.
31.(2014浙江理)在8张奖券中有一、二、三等奖各1张,其余5张无奖.将这8张奖券分配给4个人,每人2张,不同的获奖情况有_____种(用数字作答).
【答案】60【解析】分情况:一种情况将有奖的奖券按2张、1张分给4个人中的2个人,种数为;另一种将3张有奖的奖券分给4个人中的3个人,种数为,则获奖情况总共有36 +24 =60(种).
考点106 二项式定理
32.【2020全国Ⅲ理14】的展开式中常数项是 (用数字作答).
【答案】
【思路导引】写出二项式展开通项,即可求得常数项.
【解析】,其二项式展开通项:
,当,解得,的展开式中常数项是:.故答案为:.
33.【2020浙江卷12】设,则 ; .
【答案】80;51
【解析】由题意可知表示的系数,即,,,,∴,故答案为:80;51.
34.【2020天津卷11】在的展开式中,的系数是_________.
【答案】10
【解析】因为的展开式的通项公式为,令,解得.所以的系数为.故答案为:.
35.(2020全国Ⅰ理8)的展开式中的系数为 ( )
A. B. C. D.
【答案】C
【解析】展开式的通项公式为(且),∴与展开式的乘积可表示为:或,在中,令,可得:,该项中的系数为,在中,令,可得:,该项中的系数为,∴的系数为,故选C.
36.【2020北京卷3】在的展开式中,的系数为 ( )
A. B. C. D.
【答案】C
【解析】由题意展开式的通项为Tr+1=C5r(x12)5−r−2r==C5r−2rx5−r2,令r=1得x2的系数为-10,故选C.
37.(2019全国I理II理4)(1+2x2 )(1+x)4的展开式中x3的系数为
A.12 B.16 C.20 D.24
【答案】A【解析】的展开式中的系数为.故选A.
38.(2019浙江理13)在二项式的展开式中,常数项是________,系数为有理数的
项的个数是_______.
【答案】5【解析】二项式的展开式的通项为.
由,得常数项是;当r=1,3,5,7,9时,系数为有理数,所以系数为有理数的项的个数是5个.
39.(2018全国Ⅲ理)的展开式中的系数为
A.10 B.20 C.40 D.80
【答案】C【解析】,由,得,所以的系数为.故选C.
40.(2017新课标Ⅰ理)展开式中的系数为
A.15 B.20 C.30 D.35
【答案】C【解析】展开式中含的项为,故前系数为30,故选C.
41.(2017新课标Ⅲ理)的展开式中的系数为
A.80 B.40 C.40 D.80
【答案】C【解析】的展开式的通项公式为:,
当时,展开式中的系数为,
当时,展开式中的系数为,
所以的系数为,故选C.
42.(2016四川理) 设为虚数单位,则的展开式中含的项为
A.-15 B.15 C.-20 D.20
【答案】A【解析】通项,令,得含的项为,故选A.
43.(2015湖北理)已知的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为
A. B. C. D.
【答案】D【解析】因为的展开式中的第4项与第8项的二项式系数相等,所以,解得,所以二项式的展开式中奇数项的二项式系数和为.
44.(2015陕西理)二项式的展开式中的系数为15,则
A.4 B.5 C.6 D.7
【答案】C【解析】由,知,
∴,解得或(舍去),故选C.
45.(2015湖南理)已知的展开式中含的项的系数为30,则
A. B. C.6 D.-6
【答案】D【解析】,令,可得,故选D.
46.(2014浙江理)在的展开式中,记项的系数为,
则=
A.45 B.60 C.120 D.210
【答案】C【解析】由题意知,,,,因此.
47.(2014湖南理)的展开式中的系数是
A.-20 B.-5 C.5 D.20
【答案】A【解析】由二项展开式的通项可得,第四项,故的系数为-20,故选A.
48.(2014福建理)用代表红球,代表蓝球,代表黑球,由加法原理及乘法原理,从1个红球和1个篮球中取出若干个球的所有取法可由的展开式表示出来,如:“1”表示一个球都不取、“”表示取出一个红球,面“”用表示把红球和篮球都取出来.以此类推,下列各式中,其展开式可用来表示从5个无区别的红球、从5个无区别的蓝球、5个有区别的黑球中取出若干个球,且所有的篮球都取出或都不取出的所有取法的是
A.
B.
C.
D.
【答案】A【解析】分三步:第一步,5个无区别的红球可能取出0个,1个,…,5个,则有种不同的取法;第二步,5个无区别的篮球都取出或都不取出,则有种不同的取法;第三步,5个有区别的黑球看作5个不同色,从5个不同色的黑球任取0个,1个,…,5个,有种不同的取法,所以所求的取法种数为.
49.(2013辽宁理)使得的展开式中含常数项的最小的为
A. B. C. D.
【答案】B【解析】通项,常数项满足条件,所以时最小.
50.(2013江西理)展开式中的常数项为
A.80 B.-80 C.40 D.-40
【答案】C【解析】,令,解得,所以常数项为.
51.(2012安徽理)的展开式的常数项是( )
A. B. C. D.
【答案】D【解析】第一个因式取,第二个因式取得:,第一个因式取,第二个因式取得: 展开式的常数项是.
52.(2012天津理)在的二项展开式中,的系数为
A.10 B.-10 C.40 D.-40
【答案】D【解析】∵=,∴,即,
∴的系数为.
53.(2011福建理)的展开式中,的系数等于
A.80 B.40 C.20 D.10
【答案】B【解析】的展开式中含的系数等于,系数为40.答案选B.
54.(2011陕西理)(R)展开式中的常数项是
A. B. C.15 D.20
【答案】C【解析】,
令,则,所以,故选C.
55.(2019天津理理10)是展开式中的常数项为 .
【答案】28【解析】由题意,可知此二项式的展开式的通项为
.
所以当,即时,为常数项,此时.
56.(2018天津理)在的展开式中,的系数为 .
【答案】【解析】,令,得,
所以的系数为.
57.(2018浙江理)二项式的展开式的常数项是___________.
【答案】7【解析】,令,解得,所以所求常数项为.
58.(2017浙江理)已知多项式=,则=___,=___.
【答案】16,4【解析】将变换为,则其通项为,取和可得,
,令,得.
59.(2017山东理)已知的展开式中含有项的系数是,则 .
【答案】4【解析】,令得:,解得.
60.(2016山东理)若的展开式中的系数是-80,则实数a=_______.
【答案】【解析】因为,所以由,
因此
61.(2016全国I理)的展开式中,x3的系数是 .(用数字填写答案)
【答案】【解析】由得,令得,此时系数为10.
62.(2015北京理)在的展开式中,的系数为 .(用数字作答)
【答案】40【解析】由通项公式,,令,得出的系数为.
63.(2015新课标2理) 的展开式中的奇数次幂项的系数之和为32,
则=______.
【答案】3【解析】展开式的通项为,由题意可知,
,解得.
64.(2014新课标1理)的展开式中的系数为 .(用数字填写答案)
【答案】-20【解析】中,令,再令,得的系数为.
65.(2014新课标2理)的展开式中,的系数为15,则=___.(用数字填写答案)
【答案】【解析】二项展开式的通项公式为,当时,,
,则,故.
66.(2014山东理)若的展开式中项的系数为20,则的最小值为 .
【答案】2【解析】,令,得,
故,∴,当且仅当或时等号成立.
67.(2013安徽理)若的展开式中的系数为7,则实数______.
【答案】【解析】通项,所以.
68.(2012广东理)的展开式中的系数为______.(用数字作答)
【答案】20【解析】的展开式中第项为,
令得:的系数为.
69.(2012浙江理)若将函数表示为
,其中,,,…,为实数,则 .
【答案】10【解析】法一:由等式两边对应项系数相等.
即:.
法二:对等式:两边连续对x求导三次得:,再运用赋值法,令得:,即.
法三:,则.
70.(2011浙江理)设二项式的展开式中的系数为A,常数项为B,若B=4A,则的值是 .
【答案】2【解析】由题意得,
∴,,又∵,
∴,解之得,又∵,∴.
专题18 排列组合与二项式定理-2023年高考数学真题专题汇编(新高考卷): 这是一份专题18 排列组合与二项式定理-2023年高考数学真题专题汇编(新高考卷),文件包含专题18排列组合与二项式定理原卷版docx、专题18排列组合与二项式定理解析版docx等2份试卷配套教学资源,其中试卷共35页, 欢迎下载使用。
(2024届新高考数学小题专项复习)专题5 排列组合与二项式定理(单选+多选+填空)30题专项提分计划: 这是一份(2024届新高考数学小题专项复习)专题5 排列组合与二项式定理(单选+多选+填空)30题专项提分计划,文件包含2024届新高考数学小题专项复习专题5排列组合与二项式定理单选+多选+填空30题专项提分计划原卷docx、2024届新高考数学小题专项复习专题5排列组合与二项式定理单选+多选+填空30题专项提分计划解析docx等2份试卷配套教学资源,其中试卷共22页, 欢迎下载使用。
高中数学高考专题30 排列组合、二项式定理【理】(原卷版): 这是一份高中数学高考专题30 排列组合、二项式定理【理】(原卷版),共8页。












