




初中数学人教版九年级下册第二十七章 相似27.2 相似三角形27.2.2 相似三角形的性质教课内容课件ppt
展开
这是一份初中数学人教版九年级下册第二十七章 相似27.2 相似三角形27.2.2 相似三角形的性质教课内容课件ppt,共27页。PPT课件主要包含了相似三角形,相似三角形的性质,相似比,提高拓展等内容,欢迎下载使用。
1、相似三角形有哪些判定方法?
(1)平行于三角形一边的直线和其他两边(或延长线)相交所 构成的三角形与原三角形相似
(2)三边成比例的两个三角形相似
(3)两边成比例且夹角相等的两个三角形相似
(4)两角分别相等的两个三角形相似
(5)斜边和一条直角边成比例的两个直角三角形相似
2、相似三角形有什么性质?
相似三角形对应角 ,相似三角形对应边 ;
想一想:它们还有哪些性质?
思考:三角形中有各种各样的几何量,除了三边长度、三个角度外,还有高、中线、角平线、周长、面积等,如果两个三角形相似,那么它们这些量之间有什么关系呢?
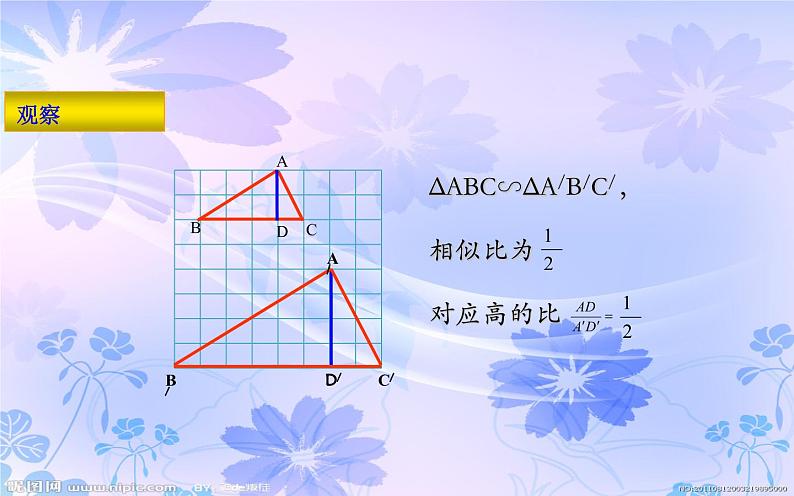
ΔABC∽ΔA/B/C/,相似比为 对应高的比
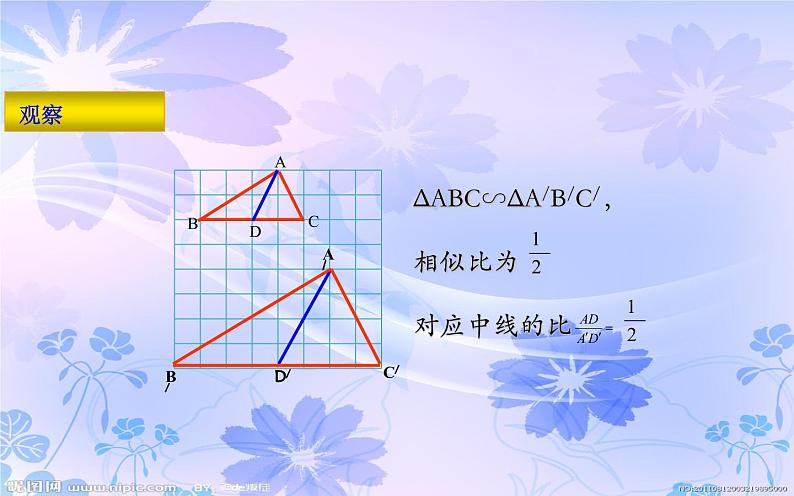
ΔABC∽ΔA/B/C/,相似比为 对应中线的比
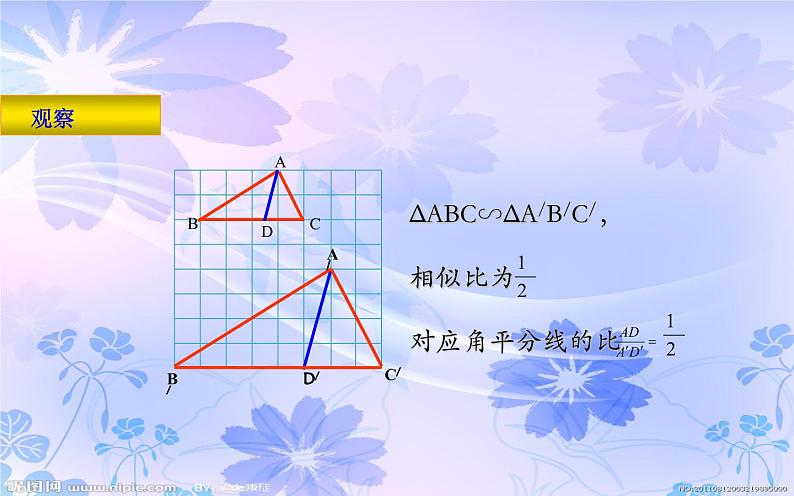
ΔABC∽ΔA/B/C/,相似比为 对应角平分线的比
可得:对应高的比 对应中线的比 对应角平分线的比
当ΔABC∽ΔA/B/C/,且相似比为 时
观察这些数据,你会有怎样的猜想呢?
猜想:相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比
①相似三角形的对应高之比等于相似比。
相似三角形的对应中线之比等于相似比。
相似三角形的对应角平线之比等于相似比。
对应高的比对应中线的比对应角平分线的比
一般地,相似三角形对应线段的比等于相似比
1、相似三角形对应边的比为2:3,那么相似比为 ,对应角的角平分线的比为 。
2、两个相似三角形相似比为1:4则对应高的比为 ,对应角的角平分线的比为 。
3、两个相似三角形对应中线的比为1:4,则相似比为 ,对应高的比为 。
问题:两个相似三角形的周长比会等于相似比吗?
如图,分别为边长为1、2、3的等边三角形,它们相似吗?
(1)与(2)的相似比为 ;(1)与(2)的周长比为 ;(2)与(3)的相似比为 ;(2)与(3)的周长比为 。
结论:相似三角形的周长比等于 。
证明:∵△ABC∽△A′B′C′且相似比为k ∴
结论:相似三角形周长之比等于相似比
已知△ABC∽△A′B′C′且相似比为k,求证: △ABC的周长:△A′B′C′的周长=k
对应高的比对应中线的比对应角平分线的比 周长的比
问题:两个相似三角形的面积之间有什么关系?
结论:相似三角形的面积比等于 。
(1)与(2)的相似比为 ;(1)与(2)的面积比为 ;(2)与(3)的相似比为 ;(2)与(3)的面积比为 。
结论:相似三角形面积之比等于相似比的平方
(1)已知ΔABC与ΔA/B/C/ 的相似比为2:3,则周长比为 ,对应边上中线之比 ,面积之比为 。(2)已知ΔABC∽ΔA/B/C/,且面积之比为9:4,则周长之比为 ,相似比 ,对应边上的高线之比 。
例1、如图在ΔABC 和ΔDEF中,AB=2DE,AC=2DF,∠A=∠D,ΔABC的周长是24,面积是 ,求ΔDEF的周长和面积。
解:在△ABC和△DEF中,
∵AB=2DE,AC=2DF,∴
又∠D=∠A,∴△DEF∽△ABC,相似比为
例2、如图,在△ABC中,D是AB的中点, DE∥BC则:
(1)S △ADE : S △ABC =
(2)S △ADE: S 梯形DBCE =
1、如图,△ABC是一块锐角三角形余料, 边BC=120毫米,高AD=80毫米,要把它加 工成正方形零件,使正方形的一边在BC上, 其余两个顶点分别在AB、AC上,这个正方 形零件的边长是多少?
解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
∵PN∥BC ∴△APN∽ △ABC
(1)相似三角形对应的 比等于相似比.
(3)相似 面积的比等于相似比的平方.
(2)相似 周长的比等于相似比.
议一议:本节课你学到了什么?
作业:P42T6、12、14
相关课件
这是一份初中数学人教版九年级下册27.2.2 相似三角形的性质图片课件ppt,共23页。PPT课件主要包含了回顾与复习,相似比对应边的比,情境引入,中线角平分线,填一填,典例分析,探索活动,又∠D=∠A,巩固练习,cm和40cm等内容,欢迎下载使用。
这是一份2020-2021学年27.2.2 相似三角形的性质示范课ppt课件,共36页。PPT课件主要包含了2相似三角形,学习目标等内容,欢迎下载使用。
这是一份初中第二十七章 相似27.2 相似三角形27.2.2 相似三角形的性质图片ppt课件,共21页。PPT课件主要包含了成比例,验证猜想,自主思考--类似验证,相似三角形,相似三角形的性质,相似比,用心观察,相似比平方,相似三角形面积的比,相似比的平方等内容,欢迎下载使用。










