2020届安徽省毛坦厂中学高三12月月考试题 数学（文）（历届）

这是一份2020届安徽省毛坦厂中学高三12月月考试题 数学（文）（历届），共8页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
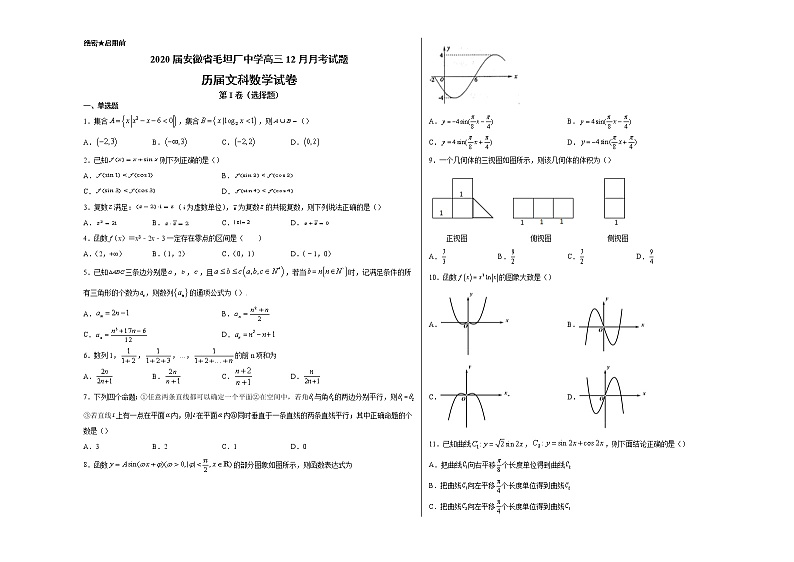
绝密★启用前2020届安徽省毛坦厂中学高三12月月考试题历届文科数学试卷第I卷（选择题)一、单选题1．集合，集合，则（）A． B． C． D．2．已知则下列正确的是（）A． B．C． D．3．复数满足：（为虚数单位），为复数的共轭复数，则下列说法正确的是（）A． B． C． D．4．函数f（x）＝x3﹣2x﹣3一定存在零点的区间是（　　）A．（2，+∞） B．（1，2） C．（0，1） D．（﹣1，0）5．已知三条边分别是，，，且，若当时，记满足条件的所有三角形的个数为，则数列的通项公式为（）.A． B．C． D．6．数列1，，，…，的前n项和为A． B． C． D．7．下列四个命题：①任意两条直线都可以确定一个平面②在空间中，若角与角的两边分别平行，则③若直线上有一点在平面内，则在平面内④同时垂直于一条直线的两条直线平行；其中正确命题的个数是（）A．3 B．2 C．1 D．08．函数的部分图象如图所示，则函数表达式为A． B．C． D．9．一个几何体的三视图如图所示，则该几何体的体积为（）正视图                  俯视图                侧视图A． B． C． D．10．函数的图象大致是（）A． B．C． D．11．已知曲线，，则下面结论正确的是（）A．把曲线向右平移个长度单位得到曲线B．把曲线向左平移个长度单位得到曲线C．把曲线向左平移个长度单位得到曲线
D．把曲线向右平移个长度单位得到曲线12．对实数和，定义运算“”： 设函数若函数的图象与轴恰有两个公共点，则实数的取值范围是（）A． B．C． D． 第II卷（非选择题) 二、填空题13．已知向量，，则在方向上的投影是________.14．设等差数列的公差不为零，若是与的等比中项，则_____.15．已知正四棱锥的顶点均在球上，且该正四棱锥的各个棱长均为，则球的表面积为____.16．函数为定义在上的奇函数，且，对于任意，都有成立.则的解集为_________.三、解答题17．在中，角所对的边分别为,且满足（2a-c）cosB=bcosC.（1）求角B的大小；（2）设，且的最大值是5，求k的值.   18．已知数列的前n项和为,且,,数列满足，.(1)求和的通项公式；(2)求数列{}的前n项和 .   19．如图1，四棱锥的底面是正方形，垂直于底面，已知四棱锥的正视图，如图2所示.（I）若M是的中点，证明：平面；（II）求棱锥的体积.  20．已知函数.（1）若函数的图象在处的切线方程为，求的值；（2）若函数在上是增函数，求实数的最大值.  21．如图，在直三棱柱中，，点是的中点.(1)求证：；(2)求证：平面.22．已知.（1）试讨论函数的单调性；（2）若使得都有恒成立，且，求满足条件的实数的取值集合.
历届文科数学12月份联考参考答案一、选择题题号123456789101112答案ADBBBBDDCADB二、填空题13．    14．4    15．8π      16．三、解答题17．（1）（2）18．（1）；  （2）【解析】（1）∵，∴当时，.当时，.∵时，满足上式，∴.又∵，∴，解得：.故，，.（2）∵，，∴①②由①-②得：∴，.考点：1.数列通项公式求解；2.错位相减法求和【点睛】求数列的通项公式主要利用，分情况求解后，验证的值是否满足关系式，解决非等差等比数列求和问题，主要有两种思路：其一，转化的思想，即将一般数列设法转化为等差或等比数列，这一思想方法往往通过通项分解（即分组求和）或错位相减来完成，其二，不能转化为等差等比数列的，往往通过裂项相消法，倒序相加法来求和，本题中，根据特点采用错位相减法求和19．（I）证明见解析；（II）.【解析】(Ⅰ)由正视图可知，∵PD⊥平面ABCD，∴ PD⊥BC又∵ABCD是正方形，∴BC⊥CD.∵，∴BC⊥平面PCD∵平面PCD，∴DM⊥BC.又是等腰三角形，E是斜边PC的中点，所以∴DM⊥PC又∵，∴DM⊥平面PBC.(Ⅱ)在平面PCD内过M作MN//PD交CD于N，所以且平面ABCD，所以棱锥M－ABD的体积为又∵棱锥A－BDM的体积等于棱锥M－ABD的体积，∴棱锥A－BDM的体积等于.【点睛】本题主要考查棱锥的体积、线面垂直的判定定理，属于中档题.解答空间几何体中垂直关系时，一般要根据已知条件把空间中的线线、线面、面面之间垂直关系进行转化，转化时要正确运用有关的定理，找出足够的条件进行推理；证明直线和平面垂直的常用方法有：（1）利用判定定理；（2）利用判定定理的推论；（3）利用面面平行的性质；（4）利用面面垂直的性质，当两个平面垂直时，在一个平面内垂直于交线的直线垂直于另一个平面.20．（1）；（2）.【解析】（1）由题意，函数.故，则，由题意，知，即.又，则.，即..（2）由题意，可知，即恒成立，恒成立…………………………………………………………………..7分设，则.令，解得.令，解得.令，解得x.在上单调递减，在上单调递增，在处取得极小值..所以 故的最大值为.………………………………………………………………………….12分【点睛】本题主要考查利用某点处的一阶导数分析得出参数的值，参变量分离方法的应用，不等式的计算能力．本题属中档题．21． (1)证明见解析；(2) 证明见解析【解析】证明：(1)∵，∴，又在直三棱柱中，有，∴平面.  因为BC1平面，∴BC. ………………………………….6分(2)设与交于点，连，易知是的中点，又是中点，∴AC1∥DP，∵平面，平面，∴AC1∥平面 . …………………………………………………………….12分【点睛】证明线与平面平行，一般可用判定定理，转化为证明线线平行，一般可通过构造平行四边形，或是三角形中位线证明线线平行，或是证明面面平行，则线面平行，在解决线面、面面平行的判定时，一般遵循从“低维”到“高维”的转化，即从“线线平行”到“线面平行”，再到“面面平行”；而在应用性质定理时，其顺序恰好相反，但也要注意，转化的方向总是由题目的具体条件而定，决不可过于“模式化”．22．（1）分类讨论，详见解析；（2）.【解析】（1）由，得…………………………..2分①当时，在上恒成立，在上单调递增；..................................................................................................4分②当时，由得，由，得，在上单调递减，在上单调递增.综上：①当时，在上单调递增，无递减区间；②当时，在上单调递减，在上单调递增…………………..6分（2）由题意函数存在最小值且，①当时，由（1）上单调递增且，当x时，，不符合条件；.......................................................................8分②当时，在上单调递减，在上单调递增，，只需即  ，记则，由得，由得，在上单调递增，在上单调递减，即满足条件的取值集合为.【点睛】本题考查了利用导数求函数的单调区间和导数的综合应用，考查了分类讨论思想和函数思想，属难题．