高中物理人教版 (新课标)选修3选修3-4第十一章 机械振动5 外力作用下的振动教学设计

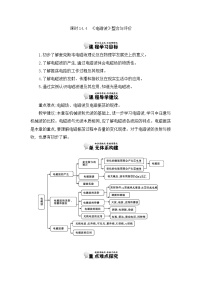
课时11.6　《机械振动》整合与评价

　　1.通过观察和分析,理解简谐运动的特征。能用公式和图象描述简谐运动的特征。

2.通过实验,探究单摆的周期与摆长的关系。知道单摆周期与摆长、重力加速度的关系。会用单摆测定重力加速度。

3.通过实验,认识受迫振动的特点。了解产生共振的条件,以及共振在技术上的应用。

重点难点:简谐运动的公式、振动图象和单摆周期公式。

教学建议:机械振动是质点运动的一种形式,通过本章的学习,要对质点运动的认识更加全面和深入。要掌握简谐运动的概念,理解简谐运动过程中各量的变化规律,并能用图象表达。掌握单摆的周期公式,并能应用其处理实际问题。

主题1:简谐运动的图象

问题:简谐运动的图象遵从正弦或余弦函数的规律,并包含着简谐运动的规律。综合本章所学知识,跟同学交流讨论从图象可以获取哪些信息。

解答:(1)从一个振动的图象形式上便可快速判断它是不是简谐运动。

(2)从图象上可直接读出振幅A和周期T;可看出任一时刻的速度方向、加速度方向、回复力方向、位移大小和方向。

(3)可以判定任一时刻速度的变化趋势,加速度和回复力大小的变化趋势,位移大小的变化趋势,等等。

(4)可以比较不同时刻位移的大小和方向、加速度和回复力的大小和方向、速度的大小和方向。

知识链接:简谐运动的图象通常称为振动图象,反映了某个质点振动位移随时间的变化规律,好像对某个质点进行“录像”一样。

　　主题2:简谐运动的表达式

问题:简谐运动的对称性体现在哪些方面?请跟同学们交流合作,总结出答案。

解答:(1)速率的对称性:系统在关于平衡位置对称的两位置具有相等的速率。

(2)时间的对称性:系统在通过关于平衡位置对称的两段位移的时间相等。在振动过程中通过任意两点A、B的时间与逆向通过这两点的时间相等。

(3)加速度的对称性:系统在关于平衡位置对称的两位置具有等大反向的加速度。

知识链接:对称性是简谐运动的重要规律,要注意理解和运用,掌握对称性可提高大家的思维能力,包括思维的多向性和严密性。

拓展一:简谐运动的图象

简谐运动的图象是周期性的正弦或余弦曲线。简谐运动的特点具有简单的周期性、重复性、对称性。对简谐运动图象进行分析,可求振幅A,周期T,任一时刻振动质点的位移、加速度的方向、速度的方向和某段时间内位移、回复力、加速度、速度、动能、势能等物理量的变化情况。

1.

水平放着的劲度系数为20 N/cm的弹簧振子,它的振动图象如图所示,则在图中A点对应的时刻(　　)。

A.振子所受的弹力大小为0.5 N,方向指向x轴的负方向

B.振子的速度方向指向x轴的正方向

C.0~4 s内振子做了1.75次全振动

D.0~4 s内振子通过的路程为0.35 cm,位移为0

问1:A点对应的形变量是多少?弹力多大?

答1:形变量为0.25 cm,弹力大小为5 N。

问2:A点对应的时刻振子的速度方向怎样?

答2:A点对应的时刻振子的速度指向x轴正方向。

问3:0~4 s内振子完成几次全振动?路程是多少?

答3:2次,4 cm。

【解析】由图可知A在t轴上方,位移x=0.25 cm,所以弹力F=-kx=-5 N,即弹力大小为5 N,方向指向x轴负方向,选项A不正确;由图可知过A点作图线的切线,该切线与x轴正方向的夹角小于90°,切线斜率为正值,即振子的速度方向指向x轴正方向,选项B正确;由图可看出,t=0、t=4 s时刻振子的位移都是最大,且都在t轴的上方,0~4 s内完成两次全振动,选项C错误;由于t=0时刻和t=4 s时刻振子都在正向最大位移处,所以0~4 s内振子的位移为零,又由于振幅为0.5 cm,在0~4 s内振子完成了2次全振动,所以在这段时间内振子通过的路程为2×4×0.5 cm=4 cm,故选项D错误。

【答案】B

【点拨】图象法是物理学上常用的一种思维方法,它能够形象直观地反映物理规律,帮助我们认识物理现象,解决物理问题。用图象来描述物体的振动时,应注意物体振动的周期、振幅、相位等。

　　2.一质点做简谐运动的振动图象如图所示。

(1)该质点振动的振幅是　　　cm;周期是　　　　s;初相位是　　　　。 

(2)写出该质点简谐运动的表达式,并求出当t=1 s时质点的位移。

【解析】(1)由图象可得出振幅、周期、初相位,即A=8 cm,T=0.2 s,φ=。

 (2)根据x=Asin(ωt+φ),ω=,知A和φ为振幅和初相位,且=10π rad/s,故质点简谐运动的表达式为x=8sin(10πt+) cm。将t=1 s代入即可求出位移x=8 cm。

【答案】(1)8　0.2　　(2)x=8sin(10πt+) cm　8 cm

　　拓展二:简谐运动的周期性和对称性

简谐运动具有周期性,即做简谐运动的质点每经过一个周期,它的位移、速度、加速度等物理量都恢复原值,其运动周期T的大小由振动系统本身的性质决定。

简谐运动的对称性是指振子经过关于平衡位置对称的两位置时,振子的位移、回复力、加速度、动能、势能、速度等均是等大的(位移、回复力、加速度的方向相反,速度的方向不确定)。

甲

3.如图甲所示,一个做简谐运动的质点先后以同样的速度通过相距为10 cm 的A、B两点,历时0.5 s。过B点后再经过t=0.5 s质点以大小相等、方向相反的速度再次通过B点,则质点振动的周期是(　　)。

A.0.5 s　 　B.1.0 s 　　C.2.0 s　 　D.4.0 s

问1:质点做简谐运动的平衡位置在哪?

答1:在AB的中点。

问2:质点从平衡位置运动到B点需多长时间?

答2:需0.25 s。

问3:质点从B点运动到最大位移处需多长时间?

答3:需0.25 s。

【解析】

乙

根据题意,由振动的对称性可知:AB的中点(设为O)为平衡位置,A、B两点对称分布于O点两侧,如图乙所示。质点从平衡位置O向右运动到B的时间应为tOB=×0.5 s=0.25 s。质点从B向右运动到达右方最大位移处(设为D)的时间tBD=×0.5 s=0.25 s,所以,质点从O到D的时间tOD=T=0.25 s+0.25 s=0.5 s,所以T=2 s。

【答案】C

【点拨】①周期性——简谐运动的物体经过一个周期或几个周期后,能恢复到原来的状态。

②对称性——简谐运动的物体具有相对平衡位置的对称性。

物体做简谐运动时,再次经过同一位置时,振子的位移相同,回复力、加速度、动能和势能也相同,速度的大小相等,但方向可相同,也可相反。在关于平衡位置对称的两个位置,动能、势能对应相等,回复力、加速度大小相等,方向相反;速度的大小相等,方向可相同,也可相反;一个做简谐运动的质点,经过时间t=nT(n为正整数),质点必回到出发点,而经过时间t=(2n+1)(n为正整数),质点所处位置必与原来位置关于平衡位置对称。

　　4.如图所示,两木块的质量分别为m、M,中间弹簧的劲度系数为k,弹簧下端与M连接,m与弹簧不连接,现将m下压一段距离释放,它将上下做简谐运动,振动过程中,m始终没有离开弹簧,试求:

(1)m振动时振幅可能的最大值。

(2)m以最大振幅振动时,M对地面的最大压力。

【解析】(1)在平衡位置时,设弹簧的压缩量为x0,则kx0=mg。

要使m振动过程中不离开弹簧,m振动的最高点不能高于弹簧原长处

所以m振动的振幅的最大值A=x0=。

(2)m以最大振幅A振动时,振动到最低点,弹簧的压缩量最大,为2A=2x0=

对M受力分析可得:FN=Mg+k·=Mg+2mg

由牛顿第三定律得,M对地面的最大压力为Mg+2mg。

【答案】(1)　(2)Mg+2mg

拓展三:单摆周期公式的应用

等效单摆的周期公式T=2π中,g'是等效重力加速度。等效重力加速度g'由单摆所在的空间位置决定,一般情况下等效重力加速度g'等于摆球静止时摆线的张力(视重)与摆球质量的比值。

5.如图所示,在水平地面上有一段光滑圆弧形槽,弧的半径是R,所对圆心角小于10°。现在在圆弧的右侧边缘M处放一个小球A,使其由静止下滑,则:

(1)球由M至O的过程中所需时间t为多少?在此过程中能量如何转化(定性说明)?

(2)若在MN圆弧上存在两点P、Q,且P、Q关于O对称,已测得球A由P直达Q所需时间为Δt,则球由Q至N的最短时间为多少?

问1:圆弧所对圆心角小于10°说明什么问题?

答1:说明小球在光滑圆弧槽上的运动可看成简谐运动,可视为等效摆。

问2:单摆的周期公式是什么?

答2:单摆的周期公式是T=2π。

问3:P、Q关于O点对称说明什么问题?

答3:P、Q关于O点对称说明由P到O和由O到Q的时间相等。

【解析】(1)由单摆周期公式T=2π知,球A的运动周期T=2π,所以tMO=T=。在由M→O的过程中球A的重力势能转化为动能。

 (2)由对称性可知tOQ=Δt,tOQ+tQN=T,联立得Q至N的最短时间tQN=-Δt。

【答案】(1)　重力势能转化为动能

(2)-Δt

【点拨】要抓住圆弧光滑且圆心角小于10°这两个条件,此隐含条件意味着小球的运动可等效为单摆,即球在圆弧上做简谐运动。从而利用简谐运动的周期性和对称性以及机械能守恒定律解决问题。本题易出现的错误是不会利用简谐运动的对称性。

　　6.已知单摆摆长为l,悬点正下方处有一个钉子,如图所示。若让摆球做小角度摆动,其周期将是多大?

【解析】该摆在通过悬点的竖直线两边的运动都可以看作简谐运动,周期分别为T1=2π和T2=π,因此该摆的周期:T=+=。

【答案】

一、物理百科

钟摆的发现

1583年的一天,伽利略早早来到教堂做礼拜。此时,教堂的大门刚刚打开,当伽利略随着三三两两的人群走入大厅时,第一束晨光才从天窗中射入教堂,因此,整个空间还是浑黑一片,礼拜还没有开始,于是他摸黑坐了下来,默默地开始了虔诚的祈祷。

忽然,伽利略觉得眼前渐渐明亮起来,地上桌椅的影子随着本身清晰度的增加在不断地晃动。他下意识地抬起头,原来,一个勤杂工在点燃教堂里的豪华的大吊灯之后,没有把它放稳,因此,大吊灯开始不停地摇摆。

原来如此。伽利略正准备继续他的祈祷,这时,他猛然意识到,大吊灯摆动的周期似乎总是恒定的,于是他马上停止了祈祷,开始进一步观察。当时由于没有一种精确的计时器,人们想测得一段精确的时间,就只能通过数着自己的脉搏来计时,当然,这种方法是很不准确的,因为不仅不同人的心率不同,即使是同一个人,在不同的条件下心率也是不同的。尽管如此,这在当时也还是人们普遍应用的计时方法。经过一段时间的按脉计时,伽利略发现,吊灯摆动的幅度虽然在逐渐减小,但周期始终是相等的。他为这一伟大的发现而兴奋,立即跑回家中。

回到家里,他先是爬上了屋顶拴了一根长长的绳子吊在地上,然后,他把一切能找到的东西,诸如茶缸、书籍、枕头、椅子都依次拴在绳子上摆动计时。经过几天的观察发现,不管绳子吊着的物体多重,也不管振动的幅度多大,只要摆长一定,周期始终是相等的,这就是单摆的“等时性”。此时伽利略年仅18岁。

二、备用试题

1.登山运动员登雪山时,不许高声叫喊,主要原因是(　　)。

A.避免产生回声

B.减小对雪山的冲击

C.避免使雪山共振

D.使登山运动员耗散能量减少

【解析】登山运动员登雪山时,山上常年积雪,雪山内部温度高,有部分雪熔化成水,对雪山积雪有润滑作用,高声叫喊,容易引起雪山共振发生雪崩。

【答案】C

2.一弹簧振子的周期为2 s,当振子从平衡位置向右运动开始计时,经12.6 s时振子的运动情况是(　　)。

A.向右减速 B.向右加速

C.向左减速 D.向左加速

　　【解析】由简谐运动的周期性可知,经12.6 s,振子振动了6个周期,整数个周期中振子重复以前的运动形式,故分析经个周期后的运动情况即可。<T<,所以振子正在向左运动,而且是向平衡位置运动,是加速运动,故D选项正确。

【答案】D

3.下表记录了某受迫振动的振幅随驱动力频率变化的关系,若该振动系统的固有频率为f固,则(　　)。

　　A.f固=60 Hz B.60 Hz<f固<70 Hz

C.50 Hz<f固<70 Hz D.以上三个答案都不对

【解析】由表中数据可知,当驱动力的频率由50 Hz增大到70 Hz的过程中,受迫振动的振幅先增大后减小,说明振动系统的固有频率f固应为50 Hz<f固<70 Hz,C正确。在60 Hz时振幅最大,但是并不一定是受迫振动的最大振幅,从表中不能得到这一结论,所以A不对。

【答案】C

4.在光滑水平面上的O点系一长为l的绝缘细线,线的另一端系一质量为m、带电荷量为q的小球,当沿细线方向上加上电场强度为E的匀强电场后,小球处于平衡状态。现给小球一垂直于细线的初速度v0,使小球在水平面上开始运动,如图所示,若v0很小,则小球第一次回到平衡位置所需时间为多大?

【解析】小球的运动类似于一单摆运动,其回复力由电场力Eq沿运动圆弧切线方向的分力提供,周期公式T=2π中,g=

小球从开始运动到第一次回到平衡位置所用时间t==π。

【答案】π

一、单项选择题(本大题共5小题,每小题6分,共30分。每小题给出的四个选项中只有一个选项正确)

1.实验室可以做“声波碎杯”的实验。用手指轻弹一只酒杯,可以听到清脆的声音,测得这声音的频率为500 Hz。将这只酒杯放在两只大功率的声波发生器之间,操作人员通过调整其发出的声波,就能使酒杯碎掉。下列说法中正确的是(　　)。

A.操作人员一定是把声波发生器的功率调到很大

B.操作人员可能是使声波发生器发出了频率很高的超声波

C.操作人员一定是同时增大了声波发生器发出声波的频率和功率

D.操作人员一定要将声波发生器发出的声波频率调到500 Hz

【解析】通过调整发生器发出的声波就能使酒杯碎掉,是利用共振的原理,因此操作人员一定要将声波发生器发出的声波频率调到500 Hz,故D选项正确。

【答案】D

2.物体做简谐运动时,下列叙述正确的是(　　)。

A.平衡位置就是回复力为零的位置

B.处于平衡位置的物体,一定处于平衡状态

C.物体到达平衡位置,合力一定为零

D.物体到达平衡位置,加速度一定为零

【解析】简谐运动的特点:F回=-kx,当物体处于平衡位置时,x=0,则F回=0,A项正确;对于做圆弧状简谐运动的单摆模型,如图所示,O点为平衡位置,在O点时,回复力为零,但物体做圆周运动,需要向心力,所以有加速度,此时,小球重力和绳拉力的合力提供向心力,故选项B、C、D错误。

【答案】A

3. 如图所示,光滑槽半径远大于小球运动的弧长,今有两个小球同时由图示位置从静止释放,O点为槽的最低点,则它们第一次相遇的地点是(　　)。

A.O点 B.O点左侧

C.O点右侧 D.无法确定

【解析】两球释放后到槽最低点前的运动为简谐运动且等效单摆模型。其周期T=2π,从释放到最低点O的时间t=相同,所以在O点相遇,选项A正确。

【答案】A

4.图示是甲、乙两个单摆做简谐运动的图象,则下列说法中正确的是(　　)。

A.甲、乙两摆的振幅之比为2∶1

B.t=2 s时,甲摆的重力势能达到最大,乙摆的动能达到最大

C.甲、乙两摆的摆长之比为4∶1

D.甲、乙两摆摆球在最低点时的向心加速度大小一定相等

【解析】从图中可以看出振幅之比为2∶1;t=2 s时,甲摆在最低点,重力势能最小,乙摆在最高点,动能最小;由图知甲、乙周期之比为1∶2,摆长之比为1∶4;甲的振幅大,摆长短,到最低点时的速度大,向心加速度大。

【答案】A

5.如图所示,一质点做简谐运动,先后以相同的速度依次通过M、N两点,历时1 s,质点通过N点后再经过1 s又第2次通过N点,在这2 s内质点通过的总路程为12 cm。则质点的振动周期和振幅分别为(　　)。

A.3 s,6 cm B.4 s,6 cm

C.4 s,9 cm D.2 s,8 cm

【解析】因质点通过M、N两点时速度相同,说明M、N两点关于平衡位置对称,由时间的对称性可知,质点由N到最大位移,与由M到最大位移的时间相等,即t1=0.5 s,则=tMN+2t1=2 s,即T=4 s,由过程的对称性可知:质点在这2 s内通过的路程恰为2A,即2A=12 cm,A=6 cm,故B正确。

【答案】B

二、多项选择题(本大题共3小题,每小题6分,共18分。每小题给出的四个选项中至少有两个选项正确,全部选对的得6分,选对但不全的得3分,有选错的得0分)

6.一质点做简谐运动的图象如图所示,下列说法正确的是(　　)。

A.质点振动频率是4 Hz

B.在10 s内质点经过的路程是20 cm

C.在5 s末,质点做简谐运动的相位为32π

D.在t=1.5 s和t=4.5 s两时刻质点的位移大小相等,都是 cm

【解析】由振动图象知,T=4 s,故f=0.25 Hz,A错误;一个周期走4个振幅,10 s为2.5个周期,故路程为4×2×2.5 cm=20 cm,B正确;由图可知,5 s末相位为,C错误;由x=2sin t可知,1.5 s和4.5 s两时刻位移均为 cm,D正确。

【答案】BD

7.图示为某一质点的振动图象,由图可知,在t1和t2两时刻|x1|>|x2|,对应的质点速度v1、v2与加速度a1、a2的关系正确的是(　　)。

A.|v1|<|v2|,方向相同

B.|v1|<|v2|,方向相反

C.|a1|>|a2|,方向相同

D.|a1|>|a2|,方向相反

【解析】在t1时刻,质点从正向最大位移处向平衡位置运动,在t2时刻,质点从平衡位置向负向最大位移处运动,故质点速度v1与v2方向相同,由于|x1|>|x2|,所以|v1|<|v2|,A正确;在t1和t2时刻,质点离开平衡位置的位移方向相反,因而回复力方向相反,加速度方向相反,但|x1|>|x2|,t1时刻回复力大于t2时刻回复力,故|a1|>|a2|,D正确。

【答案】AD

8.图示为单摆在两次受迫振动中的共振曲线,则下列说法正确的是(　　)。

A.若两次受迫振动分别在月球上和地球上进行,且摆长相同,则图线I表示月球上单摆的共振曲线

B.若两次受迫振动是在地球上同一地点进行,则两次摆长之比lⅠ∶lⅡ=4∶25

C.图线Ⅱ若是在地面上完成的,则该摆摆长约为1 m

D.若摆长均为1 m,则图线I是在地面上完成的

【解析】受迫振动的频率与固有频率无关,但当驱动力的频率与物体固有频率相等时,受迫振动的振幅最大,所以,可以根据物体做受迫振动的共振曲线判断出物体的固有频率。根据单摆振动周期公式T=2π,可以得到单摆固有频率f==,根据图象中f的信息可以推断摆长或重力加速度的变化情况。

【答案】AC

三、填空题(共2小题,共16分)

9.(8分)图示为一单摆及其振动图象,由图回答:

(1)单摆的振幅为　　　　　,频率为　　　　　,摆长为　　　　　;一周期内位移x最大的时刻为　　　　。 

(2)若从E指向G为正方向,α为最大摆角,则图象中O、A、B、C分别对应单摆中的　　　　　　　　　　点。一周期内加速度为正且减小,并与速度同方向的时间范围是　　　。势能增加且速度为正的时间范围是　　　　。 

【解析】(1)由纵坐标的最大位移可直接读出振幅为3 cm,从横坐标上可直接读出周期T=2 s,进而计算出频率f==0.5 Hz,算出摆长l=≈1 m。从图中看出位移x有最大值的时刻为0.5 s末和1.5 s末。

(2)图象中O点位移为零,O到A的过程位移为正,且增大,A处最大,历时,显然摆球是从平衡位置E起振并向G方向运动的,所以O对应E,A对应G,A到B的过程的分析方法与O到A的相同,因而O、A、B、C对应E、G、E、F点。

摆动中E、F间加速度为正,且靠近平衡位置过程中加速度逐渐减小,所以是从F向E的运动过程。在图象中为C到D的过程,时间范围是1.5 s~2.0 s。

摆球远离平衡位置时势能增加,即从E向两侧摆动,而速度为正,显然是从E向G运动的过程。在图象中为从O到A,时间范围是0~0.5 s。

【答案】(1)3 cm　0.5 Hz　1 m　0.5 s末和1.5 s末

(2)E、G、E、F　1.5 s~2.0 s　0~0.5 s

10.(8分)用单摆测定重力加速度的实验中:

(1)实验时用20分度的游标卡尺测量摆球直径,示数如图甲所示,则该摆球的直径d=　　　　cm。 

　　甲　　　　　　　　　　　　　乙

(2)接着测量到摆线的长度为l0,实验时用拉力传感器测得摆线的拉力F随时间t变化的图象如图乙所示,则通过计算,求得重力加速度的表达式为　　　　。 

(3)某小组改变摆线长度l0,测量了多组数据。在进行数据处理时,甲同学把摆线长l0作为摆长,直接利用公式求出各组重力加速度值,然后再求出平均值;乙同学作出T2-l0图象后求出斜率,然后算出重力加速度。两同学处理数据的方法对结果的影响是:甲　　　　,乙　　　　。(填“偏大”“偏小”或“无影响”) 

【解析】(1)游标卡尺为20等份,每等份为0.05 mm,故读数为(14+2×0.05) mm=14.10 mm=1.410 cm。

(2)由题图知,周期T=4t0,而摆长l=l0+,由T=2π,得g=l==。

(3)由g=知,只将l0作为摆长计算,l偏小,则g偏小;图象法是一种减小误差的方法,故作T2-l0图象对结果无影响。

【答案】(1)1.410　(2)g=　(3)偏小　无影响

四、计算题(共36分。解答应写出必要的文字说明、方程式和重要演算步骤,只写出最后答案的不能得分。有数值计算的题,答案中必须明确写出数值和单位)

11.(10分)如图所示,一块质量为2 kg的涂有炭黑的玻璃板,在拉力F的作用下竖直向上做匀变速直线运动。一个频率为5 Hz的振动方向为水平方向且固定的振针,在玻璃板上画出了如图所示的图线,量得OA=1 cm,OB=4 cm,OC=9 cm。求拉力F的大小。(不计一切摩擦阻力,取g=10 m/s2)

【解析】f=5 Hz,则T=0.2 s

OA=1 cm,AB=3 cm,BC=5 cm

因为T0=TOA=TAB=TBC==0.1 s

根据Δs=a可得:a===2 m/s2

由牛顿第二定律得:F-mg=ma

则F=mg+ma=24 N。

【答案】24 N

12.(12分)弹簧振子以O点为平衡位置,在B、C两点间做简谐运动,在t=0时刻,振子从OB间的P点以速度v向B点运动;在t=0.20 s时,振子速度第一次变为-v;在t=0.30 s 时,振子速度第二次变为-v。

(1)求弹簧振子振动的周期T。

(2)若BC之间的距离为25 cm,求振子在2.4 s内通过的路程。

【解析】(1)画示意图,如图所示。根据题意,振子从P点出发,沿路径①到达B再沿BP回到出发点P,历时0.20 s,由对称性知tBP=0.10 s;同理,tPO=tOP'=×(0.30-0.20 s)=0.05 s,故tBO=tBP+tPO=。所以T=4×(0.10+0.05) s=0.6 s。即周期为0.6 s。

(2)BC=2A=25 cm,振幅A=12.5 cm;因振子1个周期通过4A的路程,故在2.4 s=4T内通过的路程s=4×4A=200 cm。

【答案】(1)0.6 s　(2)200 cm

13.(14分)弹簧振子以O点为平衡位置在B、C两点之间做简谐运动。B、C相距20 cm。从振子处于B点开始计时,经过0.5 s振子首次到达C点。求:

(1)振子振动的周期和频率。

(2)振子在5 s内通过的路程及5 s末的位移大小。

(3)振子在B点的加速度大小跟它距O点4 cm处P点的加速度大小的比值。

【解析】(1)设振幅为A,由题意BC=2A=20 cm,所以A=10 cm。振子从B到C所用时间t=0.5 s,为周期T的一半,所以T=1 s,f==1 Hz。

(2)振子在1个周期内通过的路程为4A。故在t=5 s=5T内通过的路程s=×4A=200 cm。5 s内振子振动了5个周期,5 s末振子仍处在B点,所以它偏离平衡位置的位移大小为10 cm。

(3)振子加速度a=-x,a∝x,所以aB∶aP=xB∶xP=10∶4=5∶2。

【答案】(1)1 s　1 Hz 　(2)200 cm　10 cm 　(3)5∶2