试卷 2021年江西省吉安市吉水县中考数学一模试卷

这是一份试卷 2021年江西省吉安市吉水县中考数学一模试卷，共29页。学案主要包含了选择题，填空题等内容，欢迎下载使用。
2021年江西省吉安市吉水县中考数学一模试卷
一、选择题（本题共6小题，每小题3分，共18分）
1．（3分）在实数|﹣3|，﹣2，0，π中，最小的数是（　　）
A．|﹣3| B．﹣2 C．0 D．π
2．（3分）下列图形中，根据AB∥CD，能得到∠1＝∠2的是（　　）
A． B．
C． D．
3．（3分）一个数用科学记数法表示为2.37×105，则这个数是（　　）
A．237 B．2370 C．23700 D．237000
4．（3分）我国古代数学名著《孙子算经》中记载了一道题，大意是：有100匹马恰好拉了100片瓦，已知1匹大马能拉3片瓦，3匹小马能拉1片瓦，问有多少匹大马、多少匹小马？若设大马有x匹，小马有y匹，那么可列方程组为（　　）
A． B．
C． D．
5．（3分）如图，在△ABC中，∠A＝36°，AB＝AC，BD是△ABC的角平分线．若在边AB上截取BE＝BC，连接DE，则图中等腰三角形共有（　　）

A．2个 B．3个 C．4个 D．5个
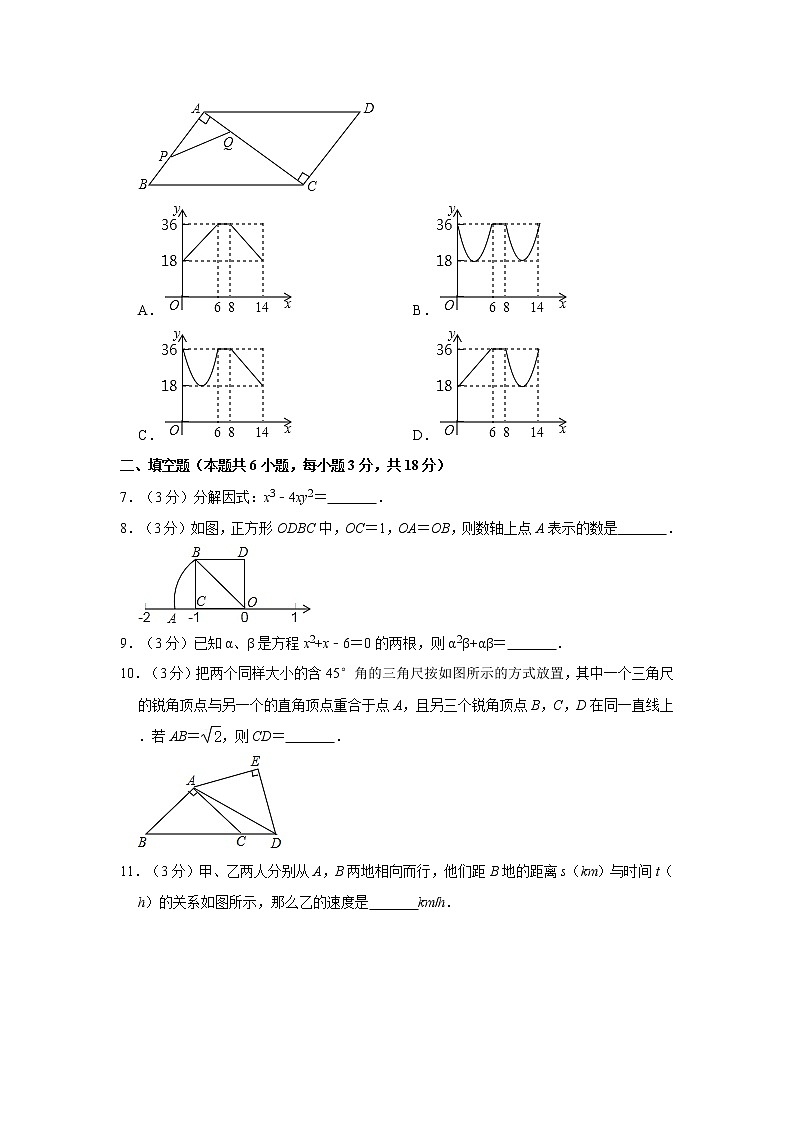
6．（3分）如图，在▱ABCD中，AB＝6，BC＝10，AB⊥AC，点P从点B出发沿着B→A→C的路径运动，同时点Q从点A出发沿着A→C→D的路径以相同的速度运动，当点P到达点C时，点Q随之停止运动，设点P运动的路程为x，y＝PQ2，下列图象中大致反映y与x之间的函数关系的是（　　）

A． B．
C． D．
二、填空题（本题共6小题，每小题3分，共18分）
7．（3分）分解因式：x3﹣4xy2＝　 　．
8．（3分）如图，正方形ODBC中，OC＝1，OA＝OB，则数轴上点A表示的数是　 　．

9．（3分）已知α、β是方程x2+x﹣6＝0的两根，则α2β+αβ＝　 　．
10．（3分）把两个同样大小的含45°角的三角尺按如图所示的方式放置，其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A，且另三个锐角顶点B，C，D在同一直线上．若AB＝，则CD＝　 　．

11．（3分）甲、乙两人分别从A，B两地相向而行，他们距B地的距离s（km）与时间t（h）的关系如图所示，那么乙的速度是　 　km/h．

12．（3分）在平面直角坐标系中，点A的坐标为（5，0），点C的坐标为（0，4），四边形ABCO为矩形，点P为线段BC上的一动点，若△POA为等腰三角形，且点P在双曲线y＝上，则k值可以是　 　．

三、（本大题5小题，每小题6分，共30分）
13．（6分）（1）求不等式组的解集．
（2）如图，已知BC平分∠ACD，且∠1＝∠2，求证：AB∥CD．

14．（6分）先化简，再求值：（﹣1）÷，其中m＝+1．
15．（6分）在“母亲节”前夕，某花店购进康乃馨和玫瑰两种鲜花，销售过程中发现康乃馨比玫瑰销量大，店主决定将玫瑰每枝降价1元促销，降价后30元可购买玫瑰的数量是原来可购买玫瑰数量的1.5倍．
（1）求降价后每枝玫瑰的售价是多少元？
（2）根据销售情况，店主用不多于900元的资金再次购进两种鲜花共500枝，康乃馨进价为2元/枝，玫瑰进价为1.5元/枝，问至少购进玫瑰多少枝？
16．（6分）为了促进“足球进校园”活动的开展，某市举行了中学生足球比赛活动．现从A，B，C三支获胜足球队中，随机抽取两支球队分别到两所边远地区学校进行交流．
（1）请用列表或画树状图的方法（只选择其中一种），表示出抽到的两支球队的所有可能结果；
（2）求出抽到B队和C队参加交流活动的概率．
17．（6分）如图是由6个形状、大小完全相同的小矩形组成的大矩形，其中小矩形的长为2，宽为1，请用无刻度的直尺在矩形中完成以下作图（保留作图痕迹，不写作法）．
（1）在图1中，画出一个面积为5的正方形；
（2）在图2中，画出一个面积为4的非特殊的平行四边形．

四、（本大题共3小题，每小题8分，共24分）
18．（8分）近几年购物的支付方式日益增多，某数学兴趣小组就此进行了抽样调查．调查结果显示，支付方式有：A微信、B支付宝、C现金、D其他，该小组对某超市一天内购买者的支付方式进行调查统计，得到如下两幅不完整的统计图．

请你根据统计图提供的信息，解答下列问题：
（1）本次一共调查了多少名购买者？
（2）请补全条形统计图；在扇形统计图中A种支付方式所对应的圆心角为　 　度．
（3）若该超市这一周内有1600名购买者，请你估计使用A和B两种支付方式的购买者共有多少名？
19．（8分）如图1，窗框和窗扇用“滑块铰链”连接，图3是图2中“滑块铰链”的平面示意图，滑轨MN安装在窗框上，托悬臂DE安装在窗扇上，交点A处装有滑块，滑块可以左右滑动，支点B，C，D始终在一直线上，延长DE交MN于点F．已知AC＝DE＝20cm，AE＝CD＝10cm，BD＝40cm．

（1）窗扇完全打开，张角∠CAB＝85°，求此时窗扇与窗框的夹角∠DFB的度数；
（2）窗扇部分打开，张角∠CAB＝60°，求此时点A，B之间的距离（精确到0.1cm）．
（参考数据：≈1.732，≈2.449）
20．（8分）如图，AB是⊙O的直径，＝，E是OB的中点，连接CE并延长到点F，使EF＝CE．连接AF交⊙O于点D，连接BD，BF．
（1）求证：直线BF是⊙O的切线；
（2）若OB＝2，求BD的长．

五、（本大题共2小题，每小题9分，共18分）
21．（9分）如图，直线y＝k1x（x≥0）与双曲线y＝（x＞0）相交于点P（2，4）．已知点A（4，0），B（0，3），连接AB，将Rt△AOB沿OP方向平移，使点O移动到点P，得到△A'PB'．过点A'作A'C∥y轴交双曲线于点C．
（1）求k1与k2的值；
（2）求直线PC的表达式；
（3）直接写出线段AB扫过的面积．

22．（9分）在△ABC中，AB＝BC，点O是AC的中点，点P是AC上的一个动点（点P不与点A，O，C重合）．过点A，点C作直线BP的垂线，垂足分别为点E和点F，连接OE，OF．
（1）如图1，请直接写出线段OE与OF的数量关系；
（2）如图2，当∠ABC＝90°时，请判断线段OE与OF之间的数量关系和位置关系，并说明理由
（3）若|CF﹣AE|＝2，EF＝2，当△POF为等腰三角形时，请直接写出线段OP的长．

六、（本大题共12分）
23．（12分）已知抛物线l：y＝ax2+bx+c（a，b，c均不为0）的顶点为M，与y轴的交点为N，我们称以N为顶点，对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线，直线MN为抛物线l的衍生直线．
（1）如图，抛物线y＝x2﹣2x﹣3的衍生抛物线的解析式是　 　，衍生直线的解析式是　 　；
（2）若一条抛物线的衍生抛物线和衍生直线分别是y＝﹣2x2+1和y＝﹣2x+1，求这条抛物线的解析式；
（3）如图，设（1）中的抛物线y＝x2﹣2x﹣3的顶点为M，与y轴交点为N，将它的衍生直线MN先绕点N旋转到与x轴平行，再沿y轴向上平移1个单位得直线n，P是直线n上的动点，是否存在点P，使△POM为直角三角形？若存在，求出所有点P的坐标；若不存在，请说明理由．


2021年江西省吉安市吉水县中考数学一模试卷
参考答案与试题解析
一、选择题（本题共6小题，每小题3分，共18分）
1．（3分）在实数|﹣3|，﹣2，0，π中，最小的数是（　　）
A．|﹣3| B．﹣2 C．0 D．π
【分析】直接利用利用绝对值的性质化简，进而比较大小得出答案．
【解答】解：在实数|﹣3|，﹣2，0，π中，
|﹣3|＝3，则﹣2＜0＜|﹣3|＜π，
故最小的数是：﹣2．
故选：B．
2．（3分）下列图形中，根据AB∥CD，能得到∠1＝∠2的是（　　）
A． B．
C． D．
【分析】两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等，据此进行判断即可．
【解答】解：A．根据AB∥CD，能得到∠1+∠2＝180°，故本选项不符合题意；
B．如图，根据AB∥CD，能得到∠3＝∠4，再根据对顶角相等，可得∠1＝∠2，故本选项符合题意；
C．根据AC∥BD，能得到∠1＝∠2，故本选项不符合题意；
D．根据AB平行CD，不能得到∠1＝∠2，故本选项不符合题意；
故选：B．

3．（3分）一个数用科学记数法表示为2.37×105，则这个数是（　　）
A．237 B．2370 C．23700 D．237000
【分析】用科学记数法表示较大的数时，一般形式为a×10n，其中1≤|a|＜10，n为整数，n的值取决于原数变成a时，小数点移动的位数，n的绝对值与小数点移动的位数相同．把2.37的小数点向右移动5位，求出这个数是多少即可．
【解答】解：2.37×105＝237000．
故选：D．
4．（3分）我国古代数学名著《孙子算经》中记载了一道题，大意是：有100匹马恰好拉了100片瓦，已知1匹大马能拉3片瓦，3匹小马能拉1片瓦，问有多少匹大马、多少匹小马？若设大马有x匹，小马有y匹，那么可列方程组为（　　）
A． B．
C． D．
【分析】设大马有x匹，小马有y匹，根据题意可得等量关系：①大马数+小马数＝100；②大马拉瓦数+小马拉瓦数＝100，根据等量关系列出方程组即可．
【解答】解：设大马有x匹，小马有y匹，由题意得：
，
故选：D．
5．（3分）如图，在△ABC中，∠A＝36°，AB＝AC，BD是△ABC的角平分线．若在边AB上截取BE＝BC，连接DE，则图中等腰三角形共有（　　）

A．2个 B．3个 C．4个 D．5个
【分析】根据已知条件分别求出图中三角形的内角度数，再根据等腰三角形的判定即可找出图中的等腰三角形．
【解答】解：∵AB＝AC，
∴△ABC是等腰三角形；
∵AB＝AC，∠A＝36°，
∴∠ABC＝∠C＝72°，
∵BD是△ABC的角平分线，
∴∠ABD＝∠DBC＝∠ABC＝36°，
∴∠A＝∠ABD＝36°，
∴BD＝AD，
∴△ABD是等腰三角形；
在△BCD中，∵∠BDC＝180°﹣∠DBC﹣∠C＝180°﹣36°﹣72°＝72°，
∴∠C＝∠BDC＝72°，
∴BD＝BC，
∴△BCD是等腰三角形；
∵BE＝BC，
∴BD＝BE，
∴△BDE是等腰三角形；
∴∠BED＝（180°﹣36°）÷2＝72°，
∴∠ADE＝∠BED﹣∠A＝72°﹣36°＝36°，
∴∠A＝∠ADE，
∴DE＝AE，
∴△ADE是等腰三角形；
∴图中的等腰三角形有5个．
故选：D．

6．（3分）如图，在▱ABCD中，AB＝6，BC＝10，AB⊥AC，点P从点B出发沿着B→A→C的路径运动，同时点Q从点A出发沿着A→C→D的路径以相同的速度运动，当点P到达点C时，点Q随之停止运动，设点P运动的路程为x，y＝PQ2，下列图象中大致反映y与x之间的函数关系的是（　　）

A． B．
C． D．
【分析】在Rt△ABC中，利用勾股定理可求出AC的长度，分0≤x≤6、6≤x≤8及8≤x≤14三种情况找出y关于x的函数关系式，对照四个选项即可得出结论．
【解答】解：在Rt△ABC中，∠BAC＝90°，AB＝6，BC＝10，
∴AC＝＝8．
当0≤x≤6时，AP＝6﹣x，AQ＝x，
∴y＝PQ2＝AP2+AQ2＝2x2﹣12x+36；
当6≤x≤8时，AP＝x﹣6，AQ＝x，
∴y＝PQ2＝（AQ﹣AP）2＝36；
当8≤x≤14时，CP＝14﹣x，CQ＝x﹣8，
∴y＝PQ2＝CP2+CQ2＝2x2﹣44x+260．
故选：B．
二、填空题（本题共6小题，每小题3分，共18分）
7．（3分）分解因式：x3﹣4xy2＝　x（x+2y）（x﹣2y）　．
【分析】原式提取x，再利用平方差公式分解即可．
【解答】解：原式＝x（x2﹣4y2）＝x（x+2y）（x﹣2y），
故答案为：x（x+2y）（x﹣2y）
8．（3分）如图，正方形ODBC中，OC＝1，OA＝OB，则数轴上点A表示的数是　﹣　．

【分析】在直角三角形中根据勾股定理求得OB的值，即OA的值，进而求出数轴上点A表示的数
【解答】解：∵OB＝＝，
∴OA＝OB＝，
∵点A在数轴上原点的左边，
∴点A表示的数是﹣，
故答案为：﹣．
9．（3分）已知α、β是方程x2+x﹣6＝0的两根，则α2β+αβ＝　12或﹣18　．
【分析】先利用根与系数的关系得到α+β＝﹣1，αβ＝﹣6，所以α2β+αβ＝αβ（α+1）＝﹣6（α+1），再解方程解方程x2+x﹣6＝0得x1＝﹣3，x2＝2，然后把α＝﹣3和α＝2分别代入计算即可．
【解答】解：根据题意得α+β＝﹣1，αβ＝﹣6，
所以α2β+αβ＝αβ（α+1）＝﹣6（α+1），
而解方程x2+x﹣6＝0得x1＝﹣3，x2＝2，
当α＝﹣3时，原式＝﹣6（﹣3+1）＝12；
当α＝2时，原式＝﹣6（2+1）＝﹣18．
故答案为12或﹣18．
10．（3分）把两个同样大小的含45°角的三角尺按如图所示的方式放置，其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A，且另三个锐角顶点B，C，D在同一直线上．若AB＝，则CD＝　﹣1　．

【分析】先利用等腰直角三角形的性质求出BC＝2，BF＝AF＝1，再利用勾股定理求出DF，即可得出结论．
【解答】解：如图，过点A作AF⊥BC于F，
在Rt△ABC中，∠B＝45°，
∴BC＝AB＝2，BF＝AF＝AB＝1，
∵两个同样大小的含45°角的三角尺，
∴AD＝BC＝2，
在Rt△ADF中，根据勾股定理得，DF＝＝
∴CD＝BF+DF﹣BC＝1+﹣2＝﹣1，
故答案为：﹣1．

11．（3分）甲、乙两人分别从A，B两地相向而行，他们距B地的距离s（km）与时间t（h）的关系如图所示，那么乙的速度是　3.6　km/h．

【分析】方法1，根据题意，甲的速度为6km/h，乙出发后2.5小时两人相遇，可以用方程思想解决问题．
方法2，先求出甲的路程与时间的函数关系，进而求出x＝4.5时，甲的速度，即可得出结论．
【解答】解法1：由题意，甲速度为6km/h．当甲开始运动时相距36km，两小时后，乙开始运动，经过2.5小时两人相遇．
设乙的速度为xkm/h，
2.5×（6+x）＝36﹣12，
解得x＝3.6，
故答案为：3.6．
解法2：由题意得，设甲的路程与时间的函数关系y＝kx+b，
把（0，36）（2，24）代入y＝kx+b，
∴，
∴，
∴甲的路程与时间的函数关系式为y＝﹣6x+36，
∵甲乙相遇时x＝4.5，
∴y＝﹣6×4.5+36＝9，
所以乙的速度为（9﹣0）÷2.5＝3.6（km/h），
故答案为：3.6．
12．（3分）在平面直角坐标系中，点A的坐标为（5，0），点C的坐标为（0，4），四边形ABCO为矩形，点P为线段BC上的一动点，若△POA为等腰三角形，且点P在双曲线y＝上，则k值可以是　10或12或8　．

【分析】当PA＝PO时，根据P在OA的垂直平分线上，得到P的坐标；当OP＝OA＝5时，由勾股定理求出CP即可；当AP＝AO＝5时，同理求出BP、CP，即可得出P的坐标，然后把P的坐标代入线y＝，即可求得k的值．
【解答】解：∵点A的坐标为（5，0），点C的坐标为（0，4），
∴当PA＝PO时，P在OA的垂直平分线上，P的坐标是（2.5，4）；
当OP＝OA＝5时，由勾股定理得：CP＝＝3，P的坐标是（3，4）；
当AP＝AO＝5时，同理BP＝3，CP＝5﹣3＝2，P的坐标是（2，4）．
∵点P在双曲线y＝上，
∴k＝2.5×4＝10或k＝3×4＝12或k＝2×4＝8，
故答案为10或12或8．
三、（本大题5小题，每小题6分，共30分）
13．（6分）（1）求不等式组的解集．
（2）如图，已知BC平分∠ACD，且∠1＝∠2，求证：AB∥CD．

【分析】（1）分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．
（2）由BC平分∠ACD知∠1＝∠BCD，再结合∠1＝∠2知∠2＝∠BCD，从而得证．
【解答】解：（1）解不等式①得：x＞1，
解不等式②得：x＞2，
∴不等式组的解集为x＞2；

（2）∵BC平分∠ACD，
∴∠1＝∠BCD．
又∵∠1＝∠2，
∴∠2＝∠BCD．
∴AB∥CD．
14．（6分）先化简，再求值：（﹣1）÷，其中m＝+1．
【分析】根据分式的减法和除法可以化简题目中的式子，然后将m的值代入即可解答本题．
【解答】解：（﹣1）÷
＝
＝
＝，
当m＝+1时，原式＝．
15．（6分）在“母亲节”前夕，某花店购进康乃馨和玫瑰两种鲜花，销售过程中发现康乃馨比玫瑰销量大，店主决定将玫瑰每枝降价1元促销，降价后30元可购买玫瑰的数量是原来可购买玫瑰数量的1.5倍．
（1）求降价后每枝玫瑰的售价是多少元？
（2）根据销售情况，店主用不多于900元的资金再次购进两种鲜花共500枝，康乃馨进价为2元/枝，玫瑰进价为1.5元/枝，问至少购进玫瑰多少枝？
【分析】（1）可设降价后每枝玫瑰的售价是x元，根据等量关系：降价后30元可购买玫瑰的数量＝原来购买玫瑰数量的1.5倍，列出方程求解即可；
（2）可设购进玫瑰y枝，根据不等量关系：购进康乃馨的钱数+购进玫瑰的钱数≤900元，列出不等式求解即可．
【解答】解：（1）设降价后每枝玫瑰的售价是x元，依题意有
＝×1.5，
解得：x＝2．
经检验，x＝2是原方程的解．
答：降价后每枝玫瑰的售价是2元．
（2）设购进玫瑰y枝，依题意有
2（500﹣y）+1.5y≤900，
解得：y≥200．
答：至少购进玫瑰200枝．
16．（6分）为了促进“足球进校园”活动的开展，某市举行了中学生足球比赛活动．现从A，B，C三支获胜足球队中，随机抽取两支球队分别到两所边远地区学校进行交流．
（1）请用列表或画树状图的方法（只选择其中一种），表示出抽到的两支球队的所有可能结果；
（2）求出抽到B队和C队参加交流活动的概率．
【分析】（1）列表得出所有等可能结果；
（2）从表格中得出抽到B队和C队参加交流活动的结果数，利用概率公式求解可得．
【解答】解：（1）列表如下：

A
B
C
A

（B，A）
（C，A）
B
（A，B）

（C，B）
C
（A，C）
（B，C）

由表可知共有6种等可能的结果；

（2）由表知共有6种等可能结果，其中抽到B队和C队参加交流活动的有2种结果，
所以抽到B队和C队参加交流活动的概率为＝．
17．（6分）如图是由6个形状、大小完全相同的小矩形组成的大矩形，其中小矩形的长为2，宽为1，请用无刻度的直尺在矩形中完成以下作图（保留作图痕迹，不写作法）．
（1）在图1中，画出一个面积为5的正方形；
（2）在图2中，画出一个面积为4的非特殊的平行四边形．

【分析】（1）直接利用正方形的判定方法得出答案；
（2）直接利用平行四边形的判定方法得出答案．
【解答】解：（1）如图正方形ABCD；


（2）如图平行四边形EFGH．
四、（本大题共3小题，每小题8分，共24分）
18．（8分）近几年购物的支付方式日益增多，某数学兴趣小组就此进行了抽样调查．调查结果显示，支付方式有：A微信、B支付宝、C现金、D其他，该小组对某超市一天内购买者的支付方式进行调查统计，得到如下两幅不完整的统计图．

请你根据统计图提供的信息，解答下列问题：
（1）本次一共调查了多少名购买者？
（2）请补全条形统计图；在扇形统计图中A种支付方式所对应的圆心角为　108　度．
（3）若该超市这一周内有1600名购买者，请你估计使用A和B两种支付方式的购买者共有多少名？
【分析】（1）根据B的数量和所占的百分比可以求得本次调查的购买者的人数；
（2）根据统计图中的数据可以求得选择A和D的人数，从而可以将条形统计图补充完整，求得在扇形统计图中A种支付方式所对应的圆心角的度数；
（3）根据统计图中的数据可以计算出使用A和B两种支付方式的购买者共有多少名．
【解答】解：（1）56÷28%＝200，
即本次一共调查了200名购买者；
（2）D方式支付的有：200×20%＝40（人），
A方式支付的有：200﹣56﹣44﹣40＝60（人），
补全的条形统计图如右图所示，
在扇形统计图中A种支付方式所对应的圆心角为：360°×＝108°，
故答案为：108；
（3）1600×＝928（名），
答：使用A和B两种支付方式的购买者共有928名．

19．（8分）如图1，窗框和窗扇用“滑块铰链”连接，图3是图2中“滑块铰链”的平面示意图，滑轨MN安装在窗框上，托悬臂DE安装在窗扇上，交点A处装有滑块，滑块可以左右滑动，支点B，C，D始终在一直线上，延长DE交MN于点F．已知AC＝DE＝20cm，AE＝CD＝10cm，BD＝40cm．

（1）窗扇完全打开，张角∠CAB＝85°，求此时窗扇与窗框的夹角∠DFB的度数；
（2）窗扇部分打开，张角∠CAB＝60°，求此时点A，B之间的距离（精确到0.1cm）．
（参考数据：≈1.732，≈2.449）
【分析】（1）根据平行四边形的判定和性质可以解答本题；
（2）根据锐角三角函数和题意可以求得AB的长，从而可以解答本题．
【解答】解：（1）∵AC＝DE＝20cm，AE＝CD＝10cm，
∴四边形ACDE是平行四边形，
∴AC∥DE，
∴∠DFB＝∠CAB，
∵∠CAB＝85°，
∴∠DFB＝85°；
（2）作CG⊥AB于点G，
∵AC＝20，∠CGA＝90°，∠CAB＝60°，
∴CG＝，AG＝10，
∵BD＝40，CD＝10，
∴CB＝30，
∴BG＝＝，
∴AB＝AG+BG＝10+10≈10+10×2.449＝34.49≈34.5cm，
即A、B之间的距离约为34.5cm．

20．（8分）如图，AB是⊙O的直径，＝，E是OB的中点，连接CE并延长到点F，使EF＝CE．连接AF交⊙O于点D，连接BD，BF．
（1）求证：直线BF是⊙O的切线；
（2）若OB＝2，求BD的长．

【分析】（1）证明△OCE≌△BFE（SAS），可得∠OBF＝∠COE＝90°，可得结论；
（2）由（1）得：△OCE≌△BFE，则BF＝OC＝2，根据勾股定理得：AF＝2，利用面积法可得BD的长．
【解答】（1）证明：连接OC，
∵AB是⊙O的直径，＝，
∴∠BOC＝90°，
∵E是OB的中点，
∴OE＝BE，
在△OCE和△BFE中，
∵，
∴△OCE≌△BFE（SAS），
∴∠OBF＝∠COE＝90°，
∴直线BF是⊙O的切线；
（2）解：∵OB＝OC＝2，
由（1）得：△OCE≌△BFE，
∴BF＝OC＝2，
∴AF＝＝＝2，
∴S△ABF＝，
4×2＝2•BD，
∴BD＝．

五、（本大题共2小题，每小题9分，共18分）
21．（9分）如图，直线y＝k1x（x≥0）与双曲线y＝（x＞0）相交于点P（2，4）．已知点A（4，0），B（0，3），连接AB，将Rt△AOB沿OP方向平移，使点O移动到点P，得到△A'PB'．过点A'作A'C∥y轴交双曲线于点C．
（1）求k1与k2的值；
（2）求直线PC的表达式；
（3）直接写出线段AB扫过的面积．

【分析】（1）把点P（2，4）代入直线y＝k1x，把点P（2，4）代入双曲线y＝，可得k1与k2的值；
（2）根据平移的性质，求得C（6，），再运用待定系数法，即可得到直线PC的表达式；
（3）延长A'C交x轴于D，过B'作B'E⊥y轴于E，根据△AOB≌△A'PB'，可得线段AB扫过的面积＝平行四边形POBB'的面积+平行四边形AOPA'的面积，据此可得线段AB扫过的面积．
【解答】解：（1）把点P（2，4）代入直线y＝k1x，可得4＝2k1，
∴k1＝2，
把点P（2，4）代入双曲线y＝，可得k2＝2×4＝8；

（2）∵A（4，0），B（0，3），
∴AO＝4，BO＝3，
如图，延长A'C交x轴于D，
由平移可得，A'P＝AO＝4，
又∵A'C∥y轴，P（2，4），
∴点C的横坐标为2+4＝6，
当x＝6时，y＝＝，即C（6，），
设直线PC的解析式为y＝kx+b，
把P（2，4），C（6，）代入可得
，解得，
∴直线PC的表达式为y＝﹣x+；

（3）如图，延长A'C交x轴于D，
由平移可得，A'P∥AO，
又∵A'C∥y轴，P（2，4），
∴点A'的纵坐标为4，即A'D＝4，
如图，过B'作B'E⊥y轴于E，
∵PB'∥y轴，P（2，4），
∴点B'的横坐标为2，即B'E＝2，
又∵△AOB≌△A'PB'，
∴线段AB扫过的面积＝平行四边形POBB'的面积+平行四边形AOPA'的面积＝BO×B'E+AO×A'D＝3×2+4×4＝22．

22．（9分）在△ABC中，AB＝BC，点O是AC的中点，点P是AC上的一个动点（点P不与点A，O，C重合）．过点A，点C作直线BP的垂线，垂足分别为点E和点F，连接OE，OF．
（1）如图1，请直接写出线段OE与OF的数量关系；
（2）如图2，当∠ABC＝90°时，请判断线段OE与OF之间的数量关系和位置关系，并说明理由
（3）若|CF﹣AE|＝2，EF＝2，当△POF为等腰三角形时，请直接写出线段OP的长．

【分析】（1）如图1中，延长EO交CF于K．首先证明△AOE≌△COK，推出OE＝OK即可解决问题；
（2）如图2中，延长EO交CF于K．由△ABE≌△BCF，推出BE＝CF，AE＝BF，由△AOE≌△COK，推出AE＝CK，OE＝OK，推出FK＝EF，可得△EFK是等腰直角三角形，延长即可解决问题；
（3）分两种情形分别求解即可解决问题；
【解答】解：（1）如图1中，延长EO交CF于K．

∵AE⊥BE，CF⊥BE，
∴AE∥CK，
∴∠EAO＝∠KCO，
∵OA＝OC，∠AOE＝∠COK，
∴△AOE≌△COK，
∴OE＝OK，
∵△EFK是直角三角形，
∴OF＝EK＝OE．

（2）如图2中，延长EO交CF于K．

∵∠ABC＝∠AEB＝∠CFB＝90°，
∴∠ABE+∠BAE＝90°，∠ABE+∠CBF＝90°，
∴∠BAE＝∠CBF，
∵AB＝BC，
∴△ABE≌△BCF，
∴BE＝CF，AE＝BF，
∵△AOE≌△COK，
∴AE＝CK，OE＝OK，
∴FK＝EF，
∴△EFK是等腰直角三角形，
∴OF⊥EK，OF＝OE．

（3）如图3中，延长EO交CF于K．作PH⊥OF于H．

∵|CF﹣AE|＝2，EF＝2，AE＝CK，
∴FK＝2，
在Rt△EFK中，tan∠FEK＝，
∴∠FEK＝30°，∠EKF＝60°，
∴EK＝2FK＝4，OF＝EK＝2，
∵△OPF是等腰三角形，观察图形可知，只有OF＝FP＝2，
在Rt△PHF中，PH＝PF＝1，HF＝，OH＝2﹣，
∴OP＝＝﹣

如图4中，当点P在线段OC上时，作PG⊥OF于G．

同法可得：HE＝2，OH＝OF，EF＝2，
∴tan∠HFE＝，
∴∠HFE＝30°，
∴FH＝2HE＝4，
∵OH＝OF，
∴OH＝OF＝OE＝2，
∵△OPF的等腰三角形，
∴PO＝PF，
∵PG⊥OF，
∴OG＝GF＝1，
∴OP＝＝
综上所述，OP的长为﹣或．
六、（本大题共12分）
23．（12分）已知抛物线l：y＝ax2+bx+c（a，b，c均不为0）的顶点为M，与y轴的交点为N，我们称以N为顶点，对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线，直线MN为抛物线l的衍生直线．
（1）如图，抛物线y＝x2﹣2x﹣3的衍生抛物线的解析式是　y＝﹣x2﹣3　，衍生直线的解析式是　y＝﹣x﹣3　；
（2）若一条抛物线的衍生抛物线和衍生直线分别是y＝﹣2x2+1和y＝﹣2x+1，求这条抛物线的解析式；
（3）如图，设（1）中的抛物线y＝x2﹣2x﹣3的顶点为M，与y轴交点为N，将它的衍生直线MN先绕点N旋转到与x轴平行，再沿y轴向上平移1个单位得直线n，P是直线n上的动点，是否存在点P，使△POM为直角三角形？若存在，求出所有点P的坐标；若不存在，请说明理由．

【分析】（1）衍生抛物线顶点为原抛物线与y轴的交点，则可根据顶点设顶点式方程，由衍生抛物线过原抛物线的顶点则解析式易得，MN解析式易得．
（2）已知衍生抛物线和衍生直线求原抛物线思路正好与（1）相反，根据衍生抛物线与衍生直线的两交点分别为衍生抛物线与原抛物线的交点，则可推得原抛物线顶点式，再代入经过点，即得解析式．
（3）由N（0，﹣3），衍生直线MN绕点N旋转到与x轴平行得到y＝﹣3，再向上平移1个单位即得直线y＝﹣2，所以P点可设（x，﹣2）．在坐标系中使得△POM为直角三角形一般考虑勾股定理，对于坐标系中的两点，分别过点作平行于x轴、y轴的直线，则可构成以两点间距离为斜边的直角三角形，且直角边长都为两点横纵坐标差的绝对值．进而我们可以先算出三点所成三条线的平方，然后组合构成满足勾股定理的三种情况，易得P点坐标．
【解答】解：（1）∵抛物线y＝x2﹣2x﹣3过（0，﹣3），
∴设其衍生抛物线为y＝ax2﹣3，
∵y＝x2﹣2x﹣3＝x2﹣2x+1﹣4＝（x﹣1）2﹣4，
∴衍生抛物线为y＝ax2﹣3过抛物线y＝x2﹣2x﹣3的顶点（1，﹣4），
∴﹣4＝a•1﹣3，
解得 a＝﹣1，
∴衍生抛物线为y＝﹣x2﹣3．
设衍生直线为y＝kx+b，
∵y＝kx+b过（0，﹣3），（1，﹣4），
∴，
∴，
∴衍生直线为y＝﹣x﹣3．

（2）∵衍生抛物线和衍生直线两交点分别为原抛物线与衍生抛物线的顶点，
∴将y＝﹣2x2+1和y＝﹣2x+1联立，得，
解得 或 ，
∵衍生抛物线y＝﹣2x2+1的顶点为（0，1），
∴原抛物线的顶点为（1，﹣1）．
设原抛物线为y＝a（x﹣1）2﹣1，
∵y＝a（x﹣1）2﹣1过（0，1），
∴1＝a（0﹣1）2﹣1，
解得 a＝2，
∴原抛物线为y＝2x2﹣4x+1．

（3）∵N（0，﹣3），
∴MN绕点N旋转到与x轴平行后，解析式为y＝﹣3，
∴再沿y轴向上平移1个单位得的直线n解析式为y＝﹣2．
设点P坐标为（x，﹣2），
∵O（0，0），M（1，﹣4），
∴OM2＝（xM﹣xO）2+（yO﹣yM）2＝1+16＝17，
OP2＝（|xP﹣xO|）2+（yO﹣yP）2＝x2+4，
MP2＝（|xP﹣xM|）2+（yP﹣yM）2＝（x﹣1）2+4＝x2﹣2x+5．
①当OM2＝OP2+MP2时，有17＝x2+4+x2﹣2x+5，
解得x＝或x＝，即P（，﹣2）或P（，﹣2）．
②当OP2＝OM2+MP2时，有x2+4＝17+x2﹣2x+5，
解得 x＝9，即P（9，﹣2）．
③当MP2＝OP2+OM2时，有x2﹣2x+5＝x2+4+17，
解得 x＝﹣8，即P（﹣8，﹣2）．
综上所述，当P为（，﹣2）或（，﹣2）或（9，﹣2）或（﹣8，﹣2）时，△POM为直角三角形．