试卷 北师大版初中数学章节复习7年级下册 期末模拟卷（二）（教师版+学生版）

2019-2020学年北师版七年级下学期期末模拟卷(二)

参考答案与试题解析

一、选择题(共10小题，每小题3分，共30分)

1．(2019春•温江区期末)下列计算正确的是　　

A． B． 

C． D．

【分析】分别根据同底数幂的乘法，积的乘方，同底数幂的除法法则以及完全平方公式逐一判断即可．

【解答】解：，故选项不合题意；

，故选项不合题意；

，故选项符合题意；

，故选项不合题意．

故选：．

【点睛】本题主要考查了同底数幂的乘除法，积的乘方以及完全平方公式，熟记幂的运算法则是解答本题的关键．

2．(2019•漳州模拟)下面四大手机品牌图标中，轴对称图形的是　　

A． B． 

C． D．

【分析】根据轴对称图形的概念：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．

【解答】解：、是轴对称图形，故此选项正确；

、不是轴对称图形，故此选项错误；

、不是轴对称图形，故此选项错误；

、不是轴对称图形，故此选项错误；

故选：．

【点睛】此题主要考查了轴对称图形，关键是掌握轴对称图形的概念．

3．(2019•郓城县模拟)目前世界上能制造的芯片最小工艺水平是5纳米，而我国能制造芯片的最小工艺水平是16纳米，已知1纳米米，用科学记数法将16纳米表示为　　

A．米 B．米 C．米 D．米

【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．

【解答】解：纳米米，

纳米表示为：米米．

故选：．

【点睛】本题考查用科学记数法表示较小的数，一般形式为，其中，$n$为由原数左边起第一个不为零的数字前面的0的个数所决定．

4．(2019春•历下区期末)若是一个完全平方式，则等于　　

A．6 B． C． D．

【分析】由于是一个完全平方式，则或，根据完全平方公式即可得到的值．

【解答】解：是一个完全平方式，

或，

．

故选：．

【点睛】本题是完全平方公式的应用，两数的平方和，再加上或减去它们积的2倍，就构成了一个完全平方式．此题解题的关键是利用平方项来确定这两个数．

5．(2019•市中区一模)如图，已知，平分，，则的度数是　　

A． B． C． D．

【分析】根据平行线的性质得出，，求出，即可求出．

【解答】解：，

，，

平分，

，

，

故选：．

【点睛】本题考查了平行线的性质和角平分线性质，关键是求出的度数，题目比较好，难度适中．

6．(2018•信阳二模)如图，、、、四点在一条直线上，且，，增加下列条件中的一个仍不能证明，这个条件是　　

A． B． C． D．

【分析】由可求得，结合，根据全等三角形的判定方法，逐项判断即可．

【解答】解：

，

，即，且，

当时，可得，满足，可证明全等；

当时，满足，不能证明全等；

当时，满足，可证明全等；

当时，可得，满足，可证明全等；

故选：．

【点睛】本题主要考查全等三角形的判定，掌握全等三角形的判定方法是解题的关键，即、、、和．

7．(2019春•槐荫区期末)如图，四边形为矩形，依据尺规作图的痕迹，与的度数之间的关系为　　

A． B． C． D．

【分析】依据尺规作图的痕迹，可得平分，垂直平分，根据平行线的性质以及三角形内角和定理，即可得出与的度数之间的关系为．

【解答】解：如图，四边形为矩形，

，

，

依据尺规作图的痕迹，可得平分，

，

依据尺规作图的痕迹，可得垂直平分，

，

又，

，

即与的度数之间的关系为，

故选：．

【点睛】本题考查的是作图基本作图，熟知角平分线及线段垂直平分线的作法是解答此题的关键．

8．(2019春•长清区期末)如图，在中，，平分，若，则点到的距离是　　

A．4 B．3 C．2 D．5

【分析】作于．根据角平分线的性质定理得出，代入求出即可．

【解答】解：如图，作于．

，平分交于点，

(角的平分线上的点到角的两边的距离相等)，

，

，即点到的距离是4．

故选：．

【点睛】本题主要考查了角平分线的性质的应用，注意：角平分线上的点到角两边的距离相等．

9．(2019春•高新区期末)如图，中，，的垂直平分线交于点，交的延长线于点，，则　　

A． B． C． D．

【分析】根据等腰三角形的性质得到，由三角形外角的性质得到，根据线段垂直平分线的性质得到，得到，根据三角形的内角和即可得到结论．

【解答】解：，

，

，

，

垂直平分，

，

，

，

，

故选：．

【点睛】此题考查了线段垂直平分线的性质与等边三角形的判定与性质．此题难度不大，注意掌握数形结合思想的应用．

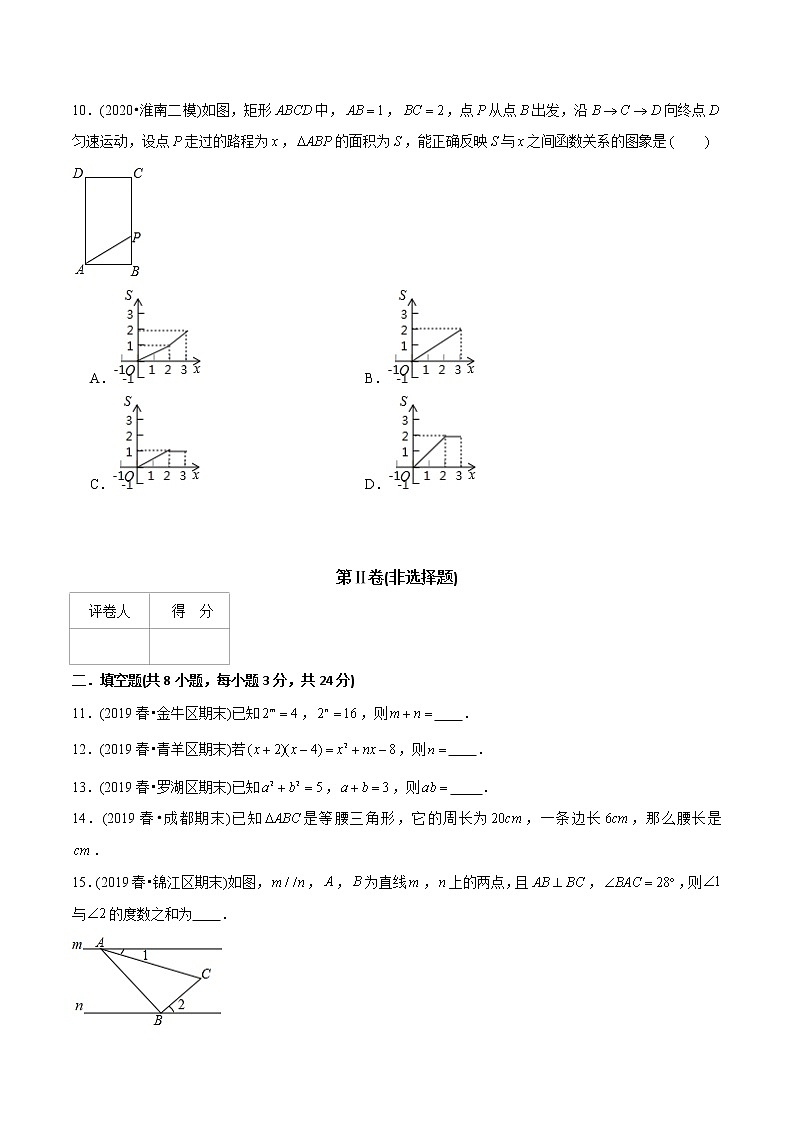
10．(2020•淮南二模)如图，矩形中，，，点从点出发，沿向终点匀速运动，设点走过的路程为，的面积为，能正确反映与之间函数关系的图象是　　

A． B． 

C． D．

【分析】要找出准确反映与之间对应关系的图象，需分析在不同阶段中随变化的情况．

【解答】解：由题意知，点从点出发，沿向终点匀速运动，则

当，，

当，，

由以上分析可知，这个分段函数的图象开始是直线一部分，最后为水平直线的一部分．

故选：．

【点睛】本题以动态的形式考查了分类讨论的思想，函数的知识和等腰直角三角形，具有很强的综合性．

二．填空题(共8小题，每小题3分，共24分)

11．(2019春•金牛区期末)已知，，则　　．

【分析】根据，，求出的值是多少，即可求出的值是多少．

【解答】解：，，

，

．

故答案为：6．

【点睛】此题主要考查了同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加，要熟练掌握，解答此题的关键是要明确：①底数必须相同；②按照运算性质，只有相乘时才是底数不变，指数相加．

12．(2019春•青羊区期末)若，则　　．

【分析】已知等式左边利用多项式乘多项式法则计算，再利用多项式相等的条件求出的值即可．

【解答】解：已知等式整理得：，

则，

故答案为：

【点睛】此题考查了多项式乘多项式，熟练掌握运算法则是解本题的关键．

13．(2019春•罗湖区期末)已知，，则　　．

【分析】把两边平方，再与相减即可．

【解答】解：，

，

，

，

解得．

【点睛】本题是对完全平方公式的考查，学生经常漏掉乘积二倍项而导致出错．

14．(2019春•成都期末)已知是等腰三角形，它的周长为，一条边长，那么腰长是　　．

【分析】当腰长时，底边，当底边时，腰长，根据三角形的三边关系，即可推出腰长．

【解答】解：等腰三角形的周长为，

当腰长时，底边，即，能构成三角形，

当底边时，腰长，即，能构成三角形，

腰长是或，

故答案为：6或7．

【点睛】本题主要考查等腰三角形的性质，三角形的三边关系，关键在于分析讨论为腰长还是底边长．

15．(2019春•锦江区期末)如图，，，为直线，上的两点，且，，则与的度数之和为　　．

【分析】如图，作直线，首先证明，求出即可

【解答】解：如图，作直线，

，

，

，，

，

，

，

，

，

．

故答案为．

【点睛】本题考查平行线的性质，垂线的性质，三角形内角和定理等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．

16．(2019春•武侯区期末)如图，为等边三角形，，则　   　度．

【分析】根据等边三角形的性质得到，，设，，根据等腰三角形的性质得到，，根据四边形的内角和列方程即可得到结论．

【解答】解：为等边三角形，

，，

设，，

，，

，

，

，，

，

，

，

，

，

故答案为：150．

【点睛】本题考查了等边三角形的性质，等腰三角形的判定和性质，三角形的内角和，正确的识别图形是解题的关键．

17．(2019春•简阳市 期末)我国南宋数学家杨辉用三角形解释二项和的乘方规律，称之为“杨辉三角”．这个三角形给出了，2，3，的展开式的系数规律(按的次数由大到小的顺序)：请依据上述规律，写出展开式中含项的系数是　   　．

【分析】首先确定项是展开式中第几项，根据杨辉三角即可解决问题．

【解答】解：由

可知，展开式中第二项为，

展开式中含项的系数是4038，

故答案为：4038．

【点睛】本题考查整式的混合运算、杨辉三角等知识，解题的关键是灵活运用杨辉三角解决问题，属于中考常考题型．

18．(2019春•成都期末)如图，在中，，，点在上，点在的延长线上，连接并延长交于点，若，，，则面积为　　．

【分析】设，则，可推得，则，所以，根据三角形面积公式可得结论．

【解答】解：，，

，

设，则，

，

，

中，，

，

，

，

，

，，

，

的面积；

故答案为：．

【点睛】本题考查了等腰直角三角形的性质，三角形的内角和定理，等腰三角形的性质，三角形的面积，推得是本题的关键．

三．解答题(共8小题，共66分)

19．(6分)(2019春•光明区期末)计算：

(1)

(2)

【分析】(1)直接利用零指数幂的性质以及绝对值的性质分别化简得出答案；

(2)直接利用整式的乘除运算法则化简得出答案．

【解答】解：(1)原式

；

(2)原式

．

【点睛】此题主要考查了整式的乘除运算，正确掌握相关运算法则是解题关键．

20．(6分)(2019春•武侯区期末)先化简，再求值．

(1)，其中，．

(2)已知，求代数式的值．

【分析】(1)根据多项式除以单项式、平方差公式可以化简题目中的式子，然后将、的值代入化简后的式子即可解答本题；

(2)根据单项式乘多项式、多项式乘多项式可以化简题目中的式子，然后根据，即可得到化简后式子的值．

【解答】解：(1)

，

当，时，

原式

；

(2)

，

，

，

原式．

【点睛】本题考查整式的化简求值，解答本题的关键是明确整式化简求值的方法．

21．(8分)(2019春•温江区期末)如图是用一些小长方形和小正方形拼成的一个大正方形．

①在图①中根据图形面积的关系写出一个用乘法公式计算的等式；

②如果，，试求图②中阴影部分的面积．

【分析】①从部分和整体两个角度求大正方形的面积即可得乘法公式计算的等式；

②先根据已知可得的值，根据直角三角形面积公式相加可得阴影部分的面积，整体代入可得结论．

【解答】解：①大正方形的面积；

②，，

，

，

，

，

图②中阴影部分的面积．

【点睛】本题主要考查了完全平方公式的几何背景，能从整体和部分两个角度求出图形的面积是解决此题的关键．

22．(8分)(2019春•锦江区期末)2019年2月3日至2019年2月20日，“第十一届成都金沙太阳节”在金沙遗址博物馆成功举办，用世界文明展览，主题灯展，园林花艺，美食演艺等一系列文化活动，与玛雅这一著名的中美洲文明结下不解之缘，为成都人打造了一个博物馆里的“文化年”，春节当天，小杰于下午2点乘车从家出发，当天按原路返回，如图，是小杰出行的过程中，他距家的距离(千米)与他离家的时间(小时)之间的图象．根据图象，完成下面问题：

(1)小杰家距金沙遗址博物馆　　千米，他乘车去金沙遗址博物馆的速度是　　千米小时；

(2)已知晚上9点时，小杰距家5千米，请通过计算说明他何时才能回到家？

(3)请直接写出小杰回家过程中与的关系式．

【分析】(1)根据函数图象进行解答：段、段、段分别表示去参观灯展去的途中，参观灯展，参观后回家的函数图象；

(2)先求出小杰回家的速度，再根据“路程速度时间”列式计算即可；

(3)根据图象解答即可．

【解答】解：(1)(千米小时)，

小杰家距金沙遗址博物馆18千米，他乘车去金沙遗址博物馆的速度是12千米小时；

故答案为：18；12；

(2)(千米时)，

(时，

，

所以小杰要在晚上9时30分才能回到家；

(3)根据图象可得，

即．

【点睛】本题考查了一次函数的应用，主要利用了待定系数法求一次函数解析式，已知函数值求自变量，准确识图，理解转折点的坐标的意义是解题的关键．

23．(8分)(2019春•成都期末)某商场为了吸引顾客，设立了可以自由转动的转盘(如图，转盘被均匀分为20份)，并规定：顾客每购买200元的商品，就能获得一次转动转盘的机会．如果转盘停止后，指针正好对准红色、黄色、绿色区域，那么顾客就可以分别获得200元、100元、50元的购物券，凭购物券可以在该商场继续购物．如果顾客不愿意转转盘，那么可以直接获得购物券30元．

(1)求转动一次转盘获得购物券的概率；

(2)某顾客在此商场购物220元，通过转转盘获得购物券和直接获得购物券，你认为哪种方式对顾客更合算？谈谈你的理由．

【分析】(1)由转盘被均匀分为20份，转动一次转盘获得购物券的有10种情况，直接利用概率公式即可求得答案；

(2)首先求得指针正好对准红色、黄色、绿色区域的概率，继而可求得转转盘的情况，继而求得答案．

【解答】解：(1)转盘被均匀分为20份，转动一次转盘获得购物券的有10种情况，

(转动一次转盘获得购物券)；

(2)(红色)，

(黄色)，

(绿色)，

(元

元元，

选择转转盘对顾客更合算．

【点睛】本题考查了概率，正确运用概率公式计算是解题的关键．

24．(8分)(2019春•福田区期末)把下面的说理过程补充完整：

已知：如图，，，线段和线段平行吗？请说明理由．

解：理由：

(已知)

即

又　       　

　          　．

　                　．

【分析】根据线段和差证明，利用两直线平行内错角相等证明，利用证明，则根据全等三角形的性质可得，最后依据内错角相等，两直线平行得出．

【解答】解：理由：

(已知)

．

．

  已知，

(两直线平行，内错角相等)．

(已知)．

(两三角形全等则它们的对应角相等)．

(内错角相等，两直线平行)．

故答案为；已知，两直线平行，内错角相等；已知；；两三角形全等则它们的对应角相等；内错角相等，两直线平行．

【点睛】本题主要考查了全等三角形的判定和性质，解题的方法是找准两三角形的对应角或边，依据判定和性质或线段的和差证明角或边相等．

25．(10分)(2019春•青羊区期末)下面的方格图是由边长为1的42个小正方形拼成的，的顶点、、均在小正方形的顶点上．

(1)作出关于直线对称的△；

(2)求的面积．

【分析】(1)利用网格特点和轴对称的性质画出点、、的对应点、、，从而得到△；

(2)利用一个矩形的面积减去三个三角形的面积去计算的面积．

【解答】解：(1)如图，△为所作；

(2)的面积．

【点睛】本题考查了作图轴对称变换：几何图形都可看做是由点组成，我们在画一个图形的轴对称图形时，也是先从确定一些特殊的对称点开始的．

26．(12分)(2019春•金牛区期末)已知，如图为的中线，分别以和为一边在的外部作等腰三角形和等腰三角形，且，，连接，

(1)如图1，若，，求的度数；

(2)如图1请探究线段和线段有何数量关系？并证明你的结论；

(3)如图2，设交于点，交于点，延长，交于点，若点为线段的中点，且，请探究和的数量关系，并证明你的结论．

【分析】(1)由等腰三角形的性质得出，由三角形内角和定理得出，推出，即可得出结果；

(2)延长至，使，连接，由中线的性质得出，由证得得出，，得出，由平行线的性质得出，证得，由证得，即可得出结论；

(3)由(2)得，，又点为中点，得出，由(2)得出，由证得得出，由已知得出，推出，由三角形内角和定理得出，即可得出结果．

【解答】(1)解：，

，

，

，，

，

，

；

(2)；理由如下：

延长至，使，连接，如图1所示：

为的中线，

，

在和中，，

，

，，

，

，

，

，

在和中，，

，

；

(3)；理由如下：

由(2)得，，又点为中点，

，

由(2)，

，

在和中，，

，

，

，

，

即：，

，

，

，

，

，

．

【点睛】本题是三角形综合题，主要考查了全等三角形的判定与性质、三角形内角和定理、等腰三角形的性质、平行线的判定与性质等知识，熟练掌握三角形内角和定理，证明三角形全等是解题的关键．