北师大版七年级下册5 利用三角形全等测距离知识点教案
展开专题12 全等三角形的模型及应用
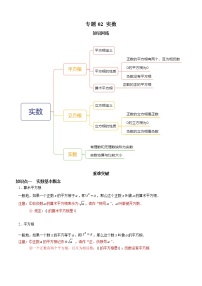
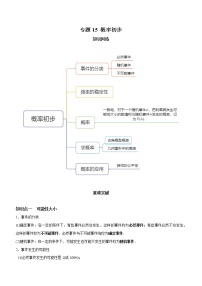
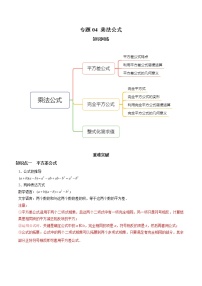
知识网络
重难突破
知识点一 全等三角形常见模型
(1)一线三等角
常见图形如下:(含特殊的一线三垂直)
(2)手拉手模型
常见图形如下:(等腰三角形、等边三角形、等腰直角三角形)
(2)半角模型
常见图形如下:(正方形、一般四边形)
(1)一线三等角
典例1
(2019春•莲湖区期末)如图1,在中,,,过点作直线,且满足于点,于点,当,在直线的同侧时,
(1)求证:.
(2)如果上面条件不变,当,在直线的异侧时,如图2,问、、之间的数量关系如何?写出结论并证明.
(3)如果上面条件不变,当,在直线的异侧时,如图3,问、、之间的数量关系如何?写出结论并证明.
【解答】(1)证明:如图1,,,
,
,
.
,
.
在和中,
,
,
,,
,
;
(2)解:,
理由:如图2,
,,
.
.
.
在和中,
,
,
,.
,
.
(3)解:,
理由是:如图3,同理易证得:,
,,
,
.
典例2
(2019春•长清区期末)是经过顶点的一条直线,,、分别是直线上两点,且.
(1)如图(1),若直线经过的内部,且、在射线上,当时,线段与有怎样的大小关系?并说明理由.
(2)如图(2),若直线经过的外部,当时,则、、三条线段之间有怎样的数量关系?并说明理由.
【解答】解:(1),理由:
,,
,(同角的余角相等)
,,
,
;
(2),理由:
,,
,(同角的补角相等)
,,
,
,,
.
(2)手拉手全等
典例1
如图,等边中,是边上的一动点,以为一边,向上作等边,连接.
(1)求证:;
(2)判断与的位置关系,并说明理由.
【解答】证明:(1)和都是等边三角形,
,,,
,
即,
在和中,
,
;
(2),理由是:
,
,
是等边三角形,
,
,
.
典例2
(2019春•金牛区期末)如图.已知∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAB+∠DAE的度数;
(3)请问线段CE、BF、DE之间有什么数量关系?请说明理由.
【解答】(1)证明:∵∠BAD=∠CAE=90°,
∴∠BAC+∠CAD=90°,∠CAD+∠DAE=90°,
∴∠BAC=∠DAE,
在△BAC和△DAE中,,
∴△BAC≌△DAE(SAS);
(2)解:∵∠CAE=90°,AC=AE,
∴∠E=45°,
由(1)知△BAC≌△DAE,
∴∠CAB=∠DAE,∠BCA=∠E=45°,
∠FAB+∠DAE=∠FAB+∠CAB=∠FAC,
∵∠AFC=90°,∠BCA=45°,
∴∠FAC=45°,
∴∠FAB+∠DAE=45°;
(3)解:CE=2BF+2DE;理由如下:
延长BF到G,使得FG=FB,连接AG,如图所示:
∵AF⊥BG,
∴AB=AG,
∴∠ABF=∠G,
∵△BAC≌△DAE,
∴AB=AD,∠CBA=∠EDA,CB=ED,
∴AG=AD,∠ABF=∠CDA,
∴∠G=∠CDA,
∵∠GCA=∠DCA=45°,
在△CGA和△CDA中,,
∴△CGA≌△CDA(AAS),
∴CG=CD,
∵CG=CB+BF+FG=CB+2BF=DE+2BF,
∴CD=2BF+DE,
∴CE=2BF+2DE.
典例3
(2019春•天桥区期末)如图1,在中,,点是边上一点(不与点、重合),以为边在的右侧作,使,,连接,设,.
(1)线段、的数量关系是 ;并说明理由;
(2)探究:当点在边上移动时,,之间有怎样的数量关系?请说明理由;
(3)如图2,若,与的延长线交于点.求证:.
【解答】解:(1)结论:.
理由:如图1中,
,,,
,
,
.
(2)结论:.
理由:如图1中,
(已证),
,
,
,,
.
(3)如图2中,
由(1)可知,
,,
,,
,
,,
,
,,
.
(3)半角模型
典例1
(2019春•罗湖区期末)四边形ABCD是正方形(四条边相等,四个角都是直角).
(1)如图1,将一个直角顶点与A点重合,角的两边分别交BC于E,交CD的延长线于F,试说明BE=DF;
(2)如图2,若将(1)中的直角改为45°角,即∠EAF=45°,E、F分别在边BC、CD上,试说明EF=BE+DF;
(3)如图3,改变(2)中的∠EAF的位置(大小不变),使E、F分别在BC、CD的延长线上,若BE=15,DF=2,试求线段EF的长.
【解答】证明:(1)∵正方形ABCD是正方形,
∴AD=AB,∠BAD=∠B=∠ADC=90°,
∵∠EAF=90°,
∴∠BAE+∠EAD=∠EAD+∠DAF=90°,
∴∠BAE=∠DAF,
在△BAE和△DAF中,
∵,
∴△ABE≌△ADF(ASA),
∴BE=DF;
(2)如图2,∵AD=AB,
将△ABE绕点A逆时针旋转90°得到△ADE',此时AB与AD重合.由旋转可得∠BAE=∠DAE',BE=DE',∠B=∠ADE'=90°.
∴∠ADF+∠ADE'=90°+90°=180°,
∴点F、D、E'在同一条直线上,
∵∠EAF=45°,
∴∠BAE+∠DAF=∠DAF+∠DAE'=45°=∠EAF,
在△EAF和△E'AF中,
∵,
∴△EAF≌△E'AF(SAS),
∴EF=E'F,
∵E'F=DF+DE'=DF+BE,
∴EF=BE+DF;
(3)将△ADF绕着点A按顺时针方向旋转90°,得△ABF′,如图3所示,
由四边形ABCD为正方形可知点B、C、F′在一条直线上,
∵∠BAF′=∠DAF,∠EAF=∠EAD+∠DAF=45°,
∴∠EAF′+∠EAD+∠DAF=90°,
∴∠EAF′=∠EAF=45°.
在△EAF和△EAF′中,
,
∴△EAF≌△EAF′(SAS),
∴EF=EF′,
∴EF=EF'=BE﹣BF'=BE﹣DF=15﹣2=13.
知识点二 全等三角形的应用
典例1
(2019春•皇姑区期末)要测量河岸相对两点、的距离,已知垂直于河岸,先在上取两点、,使,再过点作的垂线段,使点、、在一条直线上,如图,测出,,则的长是
A.2.5 B.10 C.5 D.以上都不对
【解答】解:,,
,
在和中,,
,
.
故选:.
典例2
(2019春•灵石县期末)某大学计划为新生配备如图1所示的折叠凳图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿和的长相等,是它们的中点.为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度设计为,由以上信息能求出的长度吗?如果能,请求出的长度,如果不能,请你说明理由.
【解答】解:是、的中点,
,,
在和中,,
,
,
,
.
巩固训练
一、单选题(共6小题)
1.(2019春•罗湖区期末)如图,为估计罗湖公园小池塘岸边A、B两点之间的距离,思雅学校小组在小池塘的一侧选取一点O,测得OA=28m,OB=20m,则A,B间的距离可能是( )
A.8m B.25m C.50m D.60m
【解答】解:连接AB,根据三角形的三边关系定理得:
28﹣20<AB<28+20,
即:8<AB<48,
则AB的值在8和48之间.
故选:B.
2.(2019春•市中区期末)如图,有一池塘,要测池塘两端,间的距离,可先在平地上取一个不经过池塘可以直接到达点和的点,连接并延长至,使,连接并延长至,使,连接.若量出米,则,间的距离即可求.依据是
A. B. C. D.
【解答】解:在和中,,
,
米,
故选:.
3.(2018春•槐荫区期末)两组邻边分别相等的四边形叫做“筝形”,如图,四边形是一个筝形,其中,,詹姆斯在探究筝形的性质时,得到如下结论:
①;②;③;④四边形的面积其中正确的结论有
A.1个 B.2个 C.3个 D.4个
【解答】解:在与中,
,
,
故③正确;
,
在与中,
,
,
,,
,
故①②正确;
四边形的面积,
故④正确;
故选:.
4.小明不小心把一块三角形形状的玻璃打碎成了三块,如图①②③,他想要到玻璃店去配一块大小形状完全一样的玻璃,你认为应带
A.① B.② C.③ D.①和②
【解答】解:带③去可以利用“角边角”得到全等的三角形.
故选:.
5.(2019春•青羊区期末)如图,∠ACB=90°,AC=BC,AE⊥CE于点E,BD⊥CE于点D,AE=5cm,BD=2cm,则DE的长是( )
A.8cm B.5cm C.3cm D.2cm
【解答】解:∵AE⊥CE于点E,BD⊥CE于点D,
∴∠AEC=∠D=∠ACB=90°,
∴∠A+∠ACE=90°,∠ACE+∠BCD=90°,
∴∠A=∠BCD,
∵AC=BC,
∴△ACE≌△CBD(AAS),
∴AE=CD=5cm,CE=BD=2cm,
∴DE=CD﹣CE=5﹣2=3cm.
故选:C.
6.(2019春•罗湖区期末)如图,△ABD与△AEC都是等边三角形,AB≠AC,下列结论中,正确的个数是( ),
①BE=CD;②∠BOD=60°;③∠BDO=∠CEO;④若∠BAC=90°,且DA∥BC,则BC⊥CE.
A.1 B.2 C.3 D.4
【解答】解:∵△ABD与△AEC都是等边三角形,
∴AD=AB,AE=AC,∠ADB=∠ABD=60°,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
∴∠DAC=∠BAE,
在△DAC和△BAE中,,
∴△DAC≌△BAE(SAS),
∴BE=DC,∠ADC=∠ABE,
∵∠BOD=180°﹣∠ODB﹣∠DBA﹣∠ABE=180°﹣∠ODB﹣60°﹣∠ADC=120°﹣(∠ODB+∠ADC)=120°﹣60°=60°,
∴∠BOD=60°,∴①正确;②正确;
∵△ABD与△AEC都是等边三角形,
∴∠ADB=∠AEC=60°,但根据已知不能推出∠ADC=∠AEB,
∴∠BDO=∠CEO错误,∴③错误;
∵DA∥BC,
∴∠DAB=∠ABC=60°,
∵∠BAC=90°,
∴∠ACB=30°,
∵∠ACE=60°,
∴∠ECB=90°,
∴BC⊥CE,④正确,
综上所述,①②④正确,
故选:C.
二、填空题(共5小题)
7.(2018春•历下区期中)如图,两棵大树间相距,小华从点沿走向点,行走一段时间后他到达点,此时他仰望两棵大树的顶点和,两条视线的夹角正好为,且.已知大树的高为,小华行走的速度为,小华走的时间是 .
【解答】解:,
,
,
,
,
在和中,
,
,
,
,
小华走的时间是,
故答案为:.
8.(2018春•槐荫区期末)如图,要测量河两岸相对两点、间的距离,先在过点的的垂线上取两点、,使,再在过点的垂线上取点,使、、三点在一条直线上,可证明,所以测得的长就是、两点间的距离,这里判定的理由是 .
【解答】解:,,
,
在和中,
,
.
故答案为:.
9.(2019春•商河县期末)如图,要在湖两岸,两点之间修建一座观赏桥,由于条件限制,无法直接测量、两点间的距离,于是小明想出来这样一种做法:在的垂线上取两点、,使,再定出的垂线,使,,三点在一条直线上,这时测得米,则 米.
【解答】解:根据题意可知,,
米.
故答案为:50
10.(2019春•平阴县期末)如图,为线段上一动点(不与点,重合),在同侧分别作等边和等边,与交于点,与交于点,与交于点,连接.以下五个结论:①;②;③;④;⑤,其中正确结论有 (填序号).
【解答】解:等边和等边,
,,,
,即,
在与中,,
,
,①正确,
,
,
又,
,
,
在和中,,
,
,
又,
为等边三角形,
,
,②正确,
,
③正确,
,,
,
即,
,,
,故④错误;
,
,
,
,
同理可得出,
,故⑤正确;
正确结论有:①②③⑤;
故答案为:①②③⑤.
11.(2019春•金牛区期末)如图,已知四边形ABCD中,AB=12厘米,BC=8厘米,CD=14厘米,∠B=∠C,点E为线段AB的中点.如果点P在线段BC上以3厘米秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为 厘米/秒时,能够使△BPE与以C、P、Q三点所构成的三角形全等.
【解答】解:设点P运动的时间为t秒,则BP=3t,CP=8﹣3t,
∵∠B=∠C,
∴①当BE=CP=6,BP=CQ时,△BPE与△CQP全等,
此时,6=8﹣3t,
解得t,
∴BP=CQ=2,
此时,点Q的运动速度为23厘米/秒;
②当BE=CQ=6,BP=CP时,△BPE与△CQP全等,
此时,3t=8﹣3t,
解得t,
∴点Q的运动速度为6厘米/秒;
故答案为:3或.
三、解答题(共2小题)
12.如图,中,,,直线为经过点的任一直线,于,,若,试问:
(1)与的大小关系如何?请说明理由;
(2)线段,,之间的数量之间关系如何?并说明理由.
【解答】解:(1)与的大小关系为,
理由是:,
又于,
,
;
于,于,
;
又;
,
.
(2)线段,,之间的数量之间关系为:,理由如下:
,
,,
又,
.
13.(2018秋•宿松县期末)(1)问题背景:
如图1:在四边形中,,,,、分别是,上的点且,探究图中线段、、之间的数量关系.
小王同学探究此问题的方法是,延长到点.使.连结,先证明,再证明,可得出结论,他的结论应是 ;
(2)探索延伸:如图2,若在四边形中,,.,分别是,上的点,且,上述结论是否仍然成立,并说明理由;
(3)实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心处)北偏西的处,舰艇乙在指挥中心南偏东的处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以45海里小时的速度前进,同时舰艇乙沿北偏东的方向以60海里小时的速度前进,2小时后,指挥中心观测到甲、乙两地分别到达、处,且两舰艇之间的夹角为,试求此时两舰艇之间的距离.
【解答】解:(1),证明如下:
在和中,
,
,
,,
,
,
,
在和中,
,
,
,
,
;
故答案为.
(2)结论仍然成立;
理由:延长到点.使.连结,如图2,
在和中,,
,
,,
,
,
,
在和中,
,
,
,
,
;
(3)如图3,连接,延长、相交于点,
,,
,
又,,
符合探索延伸中的条件,
结论成立,
即(海里).
答:此时两舰艇之间的距离是210海里.
初中数学北师大版八年级下册1 认识分式知识点教案: 这是一份初中数学北师大版八年级下册1 认识分式知识点教案,文件包含北师大版初中数学章节复习8年级下册专题08分式性质与运算专题测试学生版docx、北师大版初中数学章节复习8年级下册专题08分式性质与运算专题测试教师版含解析docx、北师大版初中数学章节复习8年级下册专题08分式性质与运算知识点串讲学生版docx、北师大版初中数学章节复习8年级下册专题08分式性质与运算知识点串讲教师版含解析docx等4份教案配套教学资源,其中教案共28页, 欢迎下载使用。
2020-2021学年第五章 分式与分式方程综合与测试知识点教学设计: 这是一份2020-2021学年第五章 分式与分式方程综合与测试知识点教学设计,文件包含北师大版初中数学章节复习8年级下册专题09分式方程与应用专题测试学生版docx、北师大版初中数学章节复习8年级下册专题09分式方程与应用专题测试教师版含解析docx、北师大版初中数学章节复习8年级下册专题09分式方程与应用知识点串讲学生版docx、北师大版初中数学章节复习8年级下册专题09分式方程与应用知识点串讲教师版含解析docx等4份教案配套教学资源,其中教案共29页, 欢迎下载使用。
初中数学北师大版八年级下册第四章 因式分解综合与测试知识点教学设计: 这是一份初中数学北师大版八年级下册第四章 因式分解综合与测试知识点教学设计,文件包含北师大版初中数学章节复习8年级下册专题07因式分解专题测试学生版docx、北师大版初中数学章节复习8年级下册专题07因式分解专题测试教师版含解析docx、北师大版初中数学章节复习8年级下册专题07因式分解知识点串讲学生版docx、北师大版初中数学章节复习8年级下册专题07因式分解知识点串讲教师版含解析docx等4份教案配套教学资源,其中教案共25页, 欢迎下载使用。