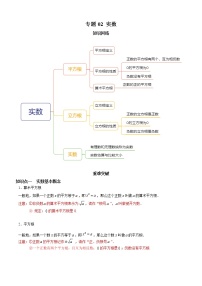
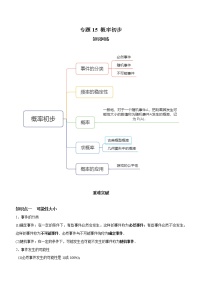
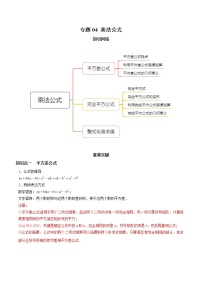
2021学年6 一元一次不等式组知识点教案设计

这是一份2021学年6 一元一次不等式组知识点教案设计，文件包含北师大版初中数学章节复习8年级下册专题05一元一次不等式组专题测试学生版docx、北师大版初中数学章节复习8年级下册专题05一元一次不等式组专题测试教师版含解析docx、北师大版初中数学章节复习8年级下册专题05一元一次不等式组知识点串讲学生版docx、北师大版初中数学章节复习8年级下册专题05一元一次不等式组知识点串讲教师版含解析docx等4份教案配套教学资源，其中教案共33页， 欢迎下载使用。


重难突破
知识点一 一元一次不等式组的解法
1、一元一次不等式组及解集
一般地，关于同一个未知数的几个一元一次不等式合在一起，就组成了一个一元一次不等式组．
一元一次不等式组中各个不等式解集的公共部分，叫做这个一元一次不等式组的解集．
注意：
一元一次不等式组的概念应满足三个条件：
①几个不等式必须含有同一个未知数；
②必须都是一元一次不等式；
③几个不等式用大括号合在一起，表示的含义是这几个不等式同时成立．
2、一元一次不等式组的解法
第一步：先分别求出不等式组中各个不等式的解集；
第二步：利用数轴求出这些解集的公共部分；
第三步：写出不等式组的解集的结论．
由两个一元一次不等式组成的不等式组，经过整理可以归结为下述四种基本类型：(表中)
典例1
(2019春•福田区期末)不等式组的解集在数轴上表示正确的是
A．B．
C．D．
典例2
(2019•济南一模)解不等式组：
知识点二 含参一元一次不等式(组)
特殊解：
求不等式组中字母参数的取值问题，可以先将字母参数当做已知处理，求出解集，与已知不等式组的解或解集的情况进行对比，进而确定字母参数的值或取值范围．
解的讨论：
已知不等式(组)，可以求出这个不等式(组)的解集；反过来，已知不等式(组)的解集，也能确定这个不等式(组)中未知的字母，把后者称为不等式(组)解集确定方法的逆用，处理这类问题时，可先求出原不等式(组)的解集，然后对照已知条件，得到关于未知字母的方程或不等式，解之即可．
注意：
这类题目的解决方法：数形结合思想．结合数轴分析解集的情况，判断字母参数的取值或取值范围．
典例1
(2019春•罗湖区期末)已知，则关于的不等式组的整数解共有
A．1个B．2个C．3个D．4个
典例2
(2019春•槐荫区期中)不等式组的解集是，则的取值范围是
B．C．D．
典例3
(2018秋•福田区校级期末)若不等式组有2个整数解，则的取值范围为
B．C．D．
典例4
(2019春•蜀山区校级期中)关于的不等式组无解，则常数的取值范围是
B．C．D．
知识点三 一元一次不等式组实际应用
一元一次不等式组的应用主要表现在两个方面：(1)通过列不等式组求未知数的取值范围；(2)通过列一元一次不等式组解决实际问题.
应用不等式组解决实际问题的一般步骤：
①审：分析题目中的已知条件和未知条件，找出题目中的不等关系；
②设：设未知数；
③列：根据不等关系列出不等式，并组成不等式组；
④解：求出不等式组的解集；
⑤答：检验解集是否合理，是否符合实际情况，作答.
典例1
(2015春•深圳校级期中)用甲乙两种原料配制成某种饮料，已知每千克的这两种原料的维生素含量及购买这两种原料的价格如表所示：现配制这种饮料，要求至少含有4200单位的维生素，且购买原料的费用不超过72元．设所需甲种原料，则可列不等式组为
A．
B．
C．
D．
典例2
(2019春•南山区校级期中)为保护环境，我市某公交公司计划购买型和型两种环保节能公交车共10辆，若购买型公交车1辆，型公交车2辆，共需400万元；若购买型公交车3辆，型公交车2辆，共需600万元．
(1)求购买型和型公交车每辆各需多少万元？
(2)预计在某线路上型和型公交车每辆年均载客量分别为60万人次和100万人次．若该公司购买型和型公交车的总费用不超过1200万元，且确保这10辆公交车在该线路的年均载客总和不少于680万人次，则该公司有哪几种购车方案？
(3)在(2)的条件下，哪种购车方案总费用最少？最少总费用是多少万元？
巩固训练
一、单选题(共6小题)
1．(2019春•天桥区期末)不等式组的解集在数轴上表示正确的是
A．B．
C．D．
2．(2019春•罗湖区期中)一元一次不等式组的解集是，则与的关系为
A．B．C．D．
3．(2019春•深圳市期中)在方程组中，若未知数，满足，则的取值范围在数轴上表示应是
A．B．C．D．
4．(2019秋•婺城区期末)关于的不等式组有四个整数解，则的取值范围是
A．B．C．D．
5．(2019•聊城)若不等式组无解，则的取值范围为
A．B．C．D．
6．(2019•福田区模拟)对于任意实数，，定义一种运算※，例如：2※．请根据上述定义解决问题：若※的整数解为
A．4B．5C．6D．7
二、填空题(共5小题)
7．(2019春•市中区期末)在平面直角坐标系中，若点在第四象限，则的取值范围是_____________．
(2019•信阳一模)如果不等式组的解集是，那么的值是 ．
9．(2018春•市南区校级期中)不等式组的解集是，则的取值范围是 ．
10．(2018•崂山区校级自主招生)若不等式组的解集是，则 ．
11．用若干辆载重量为6吨的货车运一批货物，若每辆汽车只装4吨，则剩下18吨货物；若每辆汽车只装6吨，则最后一辆货车装的货物不足5吨．若设有辆货车，则应满足的不等式组是 ．
解答题(共2小题)
12．(2019春•龙华区期末)解不等式组：，并在数轴上表示出它的解集．
13．(2019春•罗湖区期中)某工厂计划生产两种产品共10件，其生产成本和利润如表：
(1)若工厂计划获利14万元，问，两种产品应分别生产多少件？
(2)若工厂投入资金不多于44万元，且获利多于14万元，问工厂会有哪几种生产方案？请说明理由．
原料
甲
乙
维生素
600单位
100单位
原料价格
8元
4元
种产品
种产品
成本(万元件)
2
5
利润(万元件)
1
3