河北平山外国语中学 2021年中考数学模拟试卷

河北石家庄平山县外国语中学2021年中考数学模拟试卷（二）

（本卷共26小题，满分120分，考试用时120分钟）

一、选择题(本大题有16个小题，共42分.1~10小题各3分，11~16 小题各2分.在每小题给出的四个选项中，只有一项是符合题目要求的)

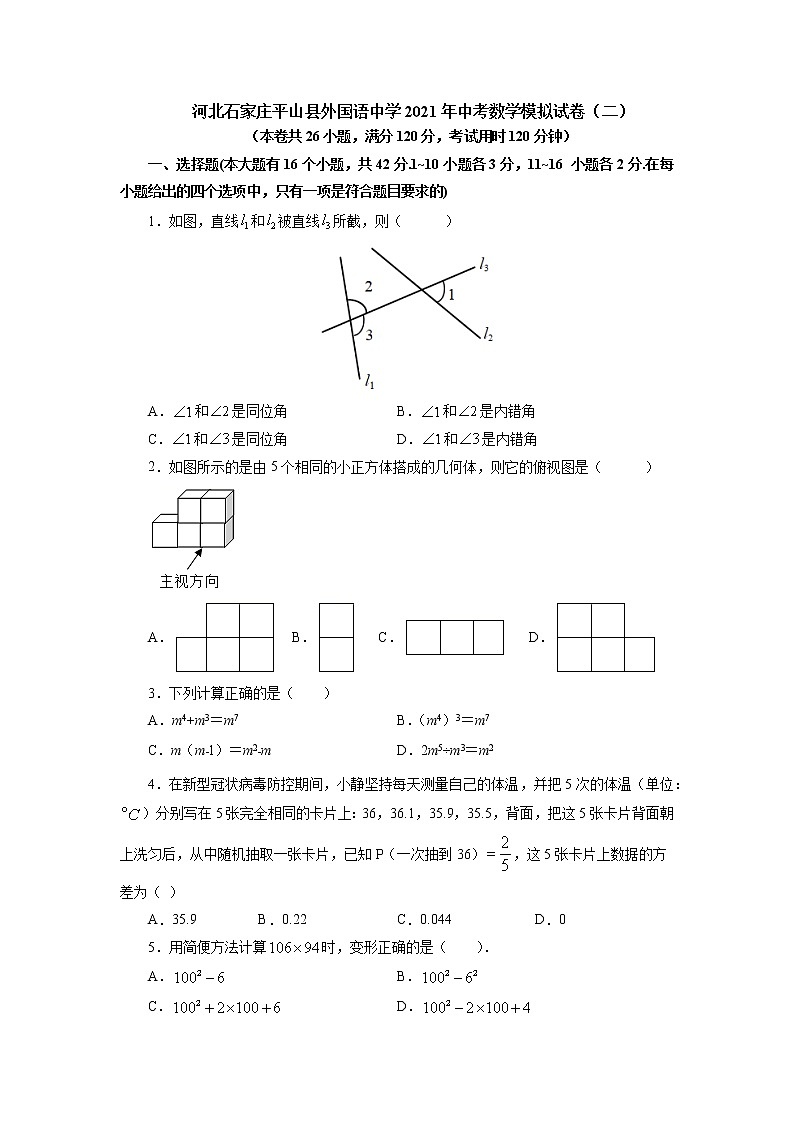
1．如图，直线和被直线所截，则（　　　）

A．和是同位角 B．和是内错角

C．和是同位角 D．和是内错角

2．如图所示的是由5个相同的小正方体搭成的几何体，则它的俯视图是（　　　）

A．  B．   C．   D．

3．下列计算正确的是（　　）

A．m4+m3＝m7 B．（m4）3＝m7

C．m（m﹣1）＝m2﹣m D．2m5÷m3＝m2

4．在新型冠状病毒防控期间，小静坚持每天测量自己的体温，并把5次的体温（单位：）分别写在5张完全相同的卡片上：36，36.1，35.9，35.5，背面，把这5张卡片背面朝上洗匀后，从中随机抽取一张卡片，已知P（一次抽到36），这5张卡片上数据的方差为（ ）

A．35.9 B．0.22 C．0.044 D．0

5．用简便方法计算时，变形正确的是（    ）．

A． B．

C． D．

6．若､使分式有意义，应满足的条件是（    ）

A．   B．，但､不都为零  C．   D．，且

7．一个数用科学记数法表示为，则原数中第一个非零数字前面“”的个数（包括小数点前面的）是（ ）

A． B． C． D．

8．如图，快艇从地出发，要到距离地10海里的地去，先沿北偏东70°方向走了8海里，到达地，然后再从地走了6海里到达地，此时快艇位于地的（    ）．

A．北偏东20°方向上 B．北偏西20°方向上

C．北偏西30°方向上 D．北偏西40°方向上

9．如图，在中，，以顶点为圆心，适当长为半径画弧，分别交，于点，，再分别以点，为圆心，大于长为半径画弧，两弧交于点，作射线交边于点，若，，则的面积是（ ）

A．7 B．30 C．14 D．60

10．如图，点，，以原点O为位似中心，把线段AB缩短为原来的一半，得到线段CD，其中点C与点A对应，点D与点B对应，则点D的横坐标为（ ）

A．2     B．2或-2       C．    D．或-

11．如图：两个同心圆，切小圆于A，切大圆于B，若，，那么两个圆所围成的圆环的面积为（    ）

A． B． C． D．

12．如图，在中，，，，E，F为垂足．设的面积为S，则的面积为（    ）

A． B． C． D．

13．我们知道下面的结论：若（，且），则．利用这个结论解决下列问题：设，，．现给出，，三者之间的三个关系式①，②，③，其中正确的是（    ）

A．① B．①② C．②③ D．①②③

14．已知是自然数，且满足，则的取值不可能是（　　　）

A．5 B．6 C．7 D．8

15．如图，在矩形中，，延长至点E使得，延长交以为直径的半圆O于点F，连结．欧几里得在《几何原本》中利用该图得到了一个重要的结论．现延长交于点G，若，，则的长为（    ）

A． B．3 C． D．

16．如图，抛物线经过点，顶点为，过点作轴的平行线，与抛物线及其对称轴分别交于点，以下结论：

①当时，；

②存在点，使；

③是定值；

④设点关于的轴的对称点为，当时，点在下方．

其中正确的是（    ）

A．①③      B．②③     C．②④     D．①④

二、填空题(本大题有3个小题,共12分.)

17．当时，二次根式的值为_____．

18．在图中，含的直角三角板的直角边，分别经过正八边形的两个顶点，则图中___________．

19．如图，在平面直角坐标系中，点和分别在直线和x轴上．都是等腰直角三角形．如果点，那么点的纵坐标是________．

20．如图，已知、，点在轴上．（1）写出点关于轴对称点的坐标______；（2）当轴平分时，点的坐标为______．

三、解答题(本大题有7个小题,共66分解答应写出文字说明、证明过程或演算步骤)

21．树兰学校初中部和小学部一起在操场做课间操．初中部排成长方形，每排人站成排；小学部排成一个边长的方阵．

（1）初中部比小学部多多少人？（用字母a，b表示）

（2）当时，该学校一共有多少名同学？

22．已知有理数-3，1．

（1）在下列数轴上，标出表示这两个数的点，并分别用A，B表示；

（2）若｜m｜=2，在数轴上表示数m的点，介于点A，B之间，在A的右侧且到点B距离为5的点表示为n．

①计算m+n-mn；

②解关于x的不等式mx+4＜n，并把解集表示在下列数轴上．

23．函数学习中，自变量取值范围及相应的函数值范围问题是大家关注的重点之一，请解决下面的问题．

（1）分别求出当时，两个函数：的最大值和最小值；

（2）若的值不大于2，求符合条件的x的范围；

（3）若，当时既无最大值，又无最小值，求a的取值范围．

24．某茶厂生产某品牌茶叶，它的成本价是每千克180元，售价是每千克230元，年销售量为10000千克．随着产量增加，为了扩大销售量，增加效益，公司决定拿出一定量的资金做广告．根据市场调查，若每年投入广告费为x（万元）时，产品的年销售量将是原销售量的y倍，且y与x之间的关系如图所示，可近似看作是抛物线的一部分．

（1）根据图象提供的信息，求y与x之间的函数关系式；

（2）求年利润S（万元）与广告费x（万元）之间的函数关系式：（年利润S=年销售总额-成本费-广告费）；

（3）问广告费x（万元）在什么范围内，公司获得的年利润S（万元）随广告费的增大而增多？

25．如图，已知A、B是线段上的两点，，，．以A为中心顺时针旋转点M，以B为中心逆时针旋转点N，使从M、N两点重合成一点C，构成，设．

（1）求x的取值范围；

（2）若为直角三角形，求x的值；

（3）探究：的最大面积？

26．已知：如图，在中，点P在上，交于一点Q．

（1）点P在的什么位置时，与四边形的面积相等？

（2）当点P在的什么位置时，将沿翻折，如图2，顶点A刚好落在上？

变式1、在图1中，连结交于点O，如图3

（1）你能得出哪些三角形相似？

（2）若，，你能求出哪些图形的面积？

变式2、在中，若，，，点P为上一点，，动点Q从A如发，沿折线以的速度运动，问经过几秒钟，截所得的新三角形与原三角形相似？

参考答案

1．C

【详解】

同位角是位于两直线及截线的同侧，内错角是位于两直线内侧及截线两侧，故和是同位角；

2．C

解：该几何体的俯视图为：

3． C

解：m4+m3不能合并，故选项A错误；

（m4）3＝m13，故选项B错误；

m（m﹣1）＝m2﹣m，故选项C正确；

2m5÷m3＝2m2，故选项D错误；

4．C

【详解】

∵抽到写有“36”的卡片的概率是，

∴卡片中36的个数为5×＝2，

则这组数据为36，36.1，35.9，35.5，36，

∵＝（36＋36.1＋35.9＋35.5＋36）＝35.9，

∴方差为×[2×（36−35.9）2＋（36.1−35.9）2＋（35.9−35.9）2＋（35.5−35.9）2]＝0.044，

5．B

【详解】

，

6．C

【详解】

由分式的分母不能为0得：，

解得，

故选：C．

7．B

解：，

∴原数中第一个非零数字前面“”的个数为9，

故选：B．

8．B

解：∵ AC=10海里，AB=8海里，BC=6海里，

根据勾股定理的逆定理可知，

∴∠ABC=90°，

∵∠DAB=70°，AD∥BE，

∴∠ABE=110°，

则∠CBE=110°－90°=20°，即点C在点B的北偏西20°方向上．

故选B

9．A

解：过点D作DE⊥AB于点E，如图所示：

∵AD平分∠CAB，∠C=90°，

∴CD=DE，

∵CD=2，

∴DE=2，

∵，

∴；

故选A．

10．D

解：以原点O为位似中心，把线段AB缩短为原来的一半，

∵点B的横坐标为3，

∴点B的对应点D的横坐标为或，

故选：D．

11． D

解：设同心圆的圆心为O，连接OA、OB和OP

∵切小圆于A，切大圆于B，

∴∠OAP=∠OBP=90°

在Rt△OAP中，OP2=OA2＋PA2

在Rt△OBP中，OP2=OB2＋PB2

∴OA2＋PA2=OB2＋PB2

∴OA2＋32=OB2＋22

∴OB2－OA2=32－22=5

∴两个圆所围成的圆环的面积为（OB2－OA2）=

12．C

解：过点F作FH⊥AE于H

∵四边形ABCD为平行四边形，

∴AD=BC，∠D=∠B=60°，∠BAD=180°－∠B=120°

∵，

∴∠BAE=90°－∠B=30°，∠DAF=90°－∠D=30°

∴∠HAF=∠BAD－∠BAE－∠DAF=60°

∵的面积为S，

∴BC·AE=S

在Rt△ADF中，AF=AD·sinD=

在Rt△AHF中，FH=AF·sin∠HAF==

∴S△AEF=AE·FH

=AE·

=·AE

=

故选C．

13．B

解：∵,

∴n=1+m,

∴m= n-1,

∵,

∴p=2+m,

∴p=n+1，m =p-2,

∴n=p-1,

①m+p=n-1+n+1=2n，故此结论正确;

②m+p=p-2+p-1=2p-3，故此结论正确;

③

=

=1，故此结论错误;

故正确结论有：①②．

故选：B．

14．D

解：原式=

∵式中有乘数3的倍数

∴

∵不能被3整除

∴原式中只能有1个3

∴原式化为

∴

∴

∵是自然数

∴

解得

当时，，得；

当时，，得；

当时，，得；

当时，，得；

15．C

解：如图，过点O作于点H，

设，

∵，

∴，，

∵G是AB的中点，

∴，

∴，

在中，，

∵，

∴，

∴，

∴，

∴，

∴，

∵，

∴．

故选：C．

16．A

解：①由题意得：，开口向上，

抛物线对称轴是，且经过点，

抛物线过轴另一个点为，

当时，；

故①正确；

②当在点时，，

，

不可能与重合，

故②不正确；

③，

故③正确；

④把代入中，，

当时，，，点在的上方，

故④不正确；

所以正确的有：①③，

17．解：当时，

，

故答案为：3．

18．

解：如图，∠1+∠2+∠3+∠4=，

∵∠C=90°

∴，

．

19．

20．（1）∵A′与A关于y轴对称，

∴点A(2，2)关于y轴的对称点A′坐标为（-2，2）；

故答案为：（-2，2）；

（2）如图，当y轴平分∠APB时，点A关于y的对称点A'在BP上，

设A'B的表达式为y=kx+b，

把A'（-2，2），B（-4，1）代入，

可得，

解得：，

∴，

令，则，

∴点P的坐标为（0，3），

故答案为：（0，3）．

21． 解：（1）∵树兰学校初中部学生人数为：

小学部学生人数为：

∴树兰学校初中部比小学部多的学生数=

答：树兰学校初中部比小学部多的学生数为名；

（2）树兰学校初中部和小学部一共的学生数=

当时，原式=

答：一共有名学生．

22．解：（1）如图：

．

（2）∵｜m｜=2，

∴m=±2，

∵在数轴上表示数m的点，介于点A，B之间，

∴m=-2，

∵在A的右侧且到点B距离为5的点表示为n，

∴n=6，

①m+n-mn=-2+6-（-2）×6=4-（-12）=4+12=16，

②由-2x+4＜6，

解得x＞-1，

表示在数轴上如图所示：．

23．解：（1）∵中，

∴y随x的增大而增大，

∴当时，y最小＝5；

当时，y最大＝9．

∵中，且抛物线的对称轴为，

∴当时，y最小＝3；

当时，y最大＝19．

（2）令，

解得：或，

∴符合条件的x的范围为或．

（3）如图所示，从下面两种情况进行讨论：

①当k＞0时，如左图得当0＜x≤2时，无最大值，有最小值，同理当a＜0时，且a≤x＜0时，y≤有最大值，无最小值；

②当k＜0时，如右图得当0＜x≤2时，无最小值，有最大值，同理当a＜0时，且a≤x＜0时，y≤有最小值，无最大值，

∴当k＜0，a＜0时，此时，既无最大值，又无最小值，

综上所述，a的取值范围是a＜0．

24．解：（1）设抛物线的解析式为

由图象可知：该抛物线过点（0,1），（1，）和（2，）

∴

解得：

∴y与x之间的函数关系式为（x≥0）；

（2）由题意可知：S=（230－180）y－x

=50（）－x

=（x≥0）

（3）∵S=（x≥0）中，-5＜0，对称轴为直线x==

∴抛物线开口向下

∴当0≤x≤时，公司获得的年利润S（万元）随广告费的增大而增多．

答：当0≤x≤时，公司获得的年利润S（万元）随广告费的增大而增多．

25．解：（1），，，

，

由旋转的性质，得，，

由三角形的三边关系，得

解不等式①得，

解不等式②得，

的取值范围是．

（2）①若AC为斜边，则，

即，

此方程无实根；

②若AB为斜边，则，

解得，满足；

③若BC为斜边，则，

解得，满足；

因此当或时，△ABC是直角三角形．

（3）在中，作于D，

设CD=h，△ABC的面积为S,则S=xh，

①若点D在线段AB上，

则+=x，

，

即x=3x−4，

，

即，

，

当x=时(满足)取最大值，从而S取最大值；

②若点D在线段MA上，

则−=x，

同理可，得

，

易知此时S<，

综合①②得，的最大面积为.

26．解：（1）∵，

∴△APQ∽△ABC

又∵与四边形的面积相等

∴,即

∴

∴点P位于处时，与四边形的面积相等

（2）将沿翻折，如图2，顶点A刚好落在上，连接AA′，交PQ于点M

由折叠性质可得，AA′⊥PQ且AM=A′M

∵，

∴△APQ∽△ABC

∴

∴

∴点P位于AB中点处时，将沿翻折，顶点A刚好落在上

变式1、（1）∵，

∴△APQ∽△ABC，△POQ∽△COB

（2）∵，

∴

∴，，

解得：，，，，

∴，

解得：，，

变式2、设t秒钟，截所得的新三角形与原三角形相似

当点Q在AC边上时，由题意可得：AP=2，AQ=t

当时，

∴，解得：

当时，

∴，解得：

当点Q在BC边上时，由题意可得：BP=4，BQ=13-t

当时，

∴，解得：

当时，

∴，解得：

综上，当秒或秒或秒或10秒钟时，截所得的新三角形与原三角形相似．