2018届中考数学考点总复习课件：第18节　等腰三角形 (共46张PPT)

这是一份2018届中考数学考点总复习课件：第18节　等腰三角形 (共46张PPT)，共46页。PPT课件主要包含了等腰三角形，等边三角形，a＋3b等内容，欢迎下载使用。

1．定义：有_____相等的三角形叫做等腰三角形．2．性质：(1)等腰三角形的两个_____相等(简称“等边对______”)；(2)等腰三角形的顶角_____线、底边上的____、底边上的_____互相重合(简称“三线合一”)．3．判定：如果一个三角形有两个___相等，那么这两个角所对的___也相等(简称“等角对_______”)．
4．定义：______都相等的三角形叫做等边三角形．5．性质：等边三角形的三个____都相等，且都等于_______.6．在直角三角形中，30°的锐角所对的直角边等于______一半．7．判定：(1)三个___都相等的三角形是等边三角形；(2)有一个角是______的______三角形是等边三角形.
腰三角形的性质与判定
【例1】(1)(2017·台州)如图，已知等腰三角形ABC，AB＝AC，若以点B为圆心，BC长为半径画弧，交腰AC于点E，则下列结论一定正确的是( )A．AE＝EC B．AE＝BEC．∠EBC＝∠BAC D．∠EBC＝∠ABE
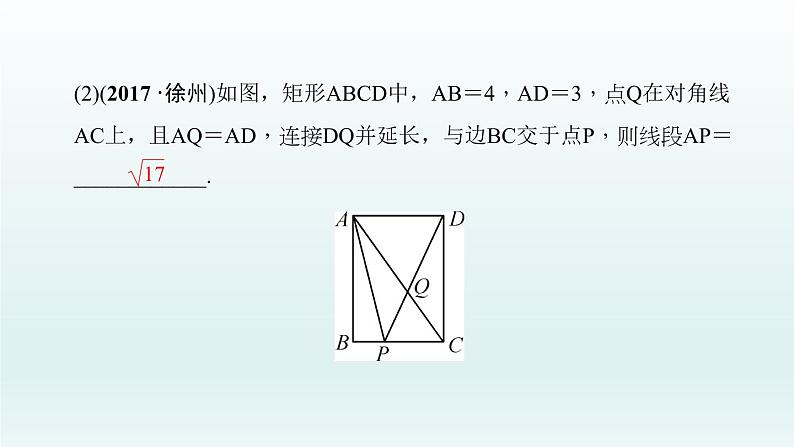
(2)(2017·徐州)如图，矩形ABCD中，AB＝4，AD＝3，点Q在对角线AC上，且AQ＝AD，连接DQ并延长，与边BC交于点P，则线段AP＝____________.
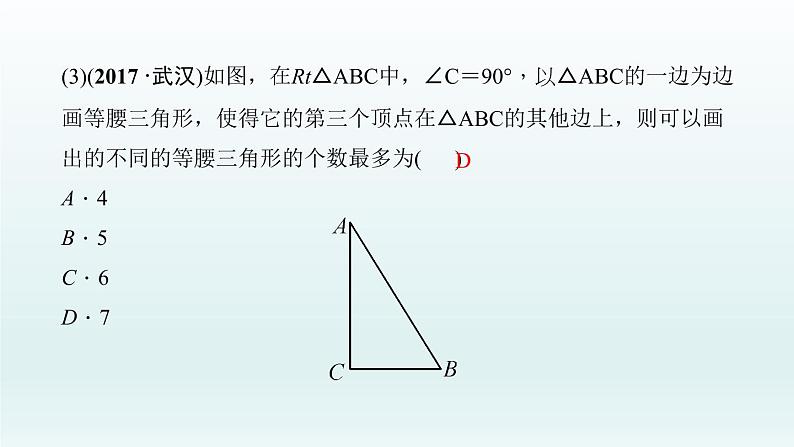
(3)(2017·武汉)如图，在Rt△ABC中，∠C＝90°，以△ABC的一边为边画等腰三角形，使得它的第三个顶点在△ABC的其他边上，则可以画出的不同的等腰三角形的个数最多为( )A．4B．5C．6D．7
【思路引导】(1)根据等腰三角形的判定和性质确定选项．(2)先根据勾股定理得到AC的长，再根据AQ＝AD，得出CP＝CQ＝2，进而得到BP的长，最后在Rt△ABP中，依据勾股定理即可得到AP的长．(3)以△ABC各顶点为圆心、各边长为半径分别画弧，或作各边的垂直平分线可作出等腰三角形．
等边三角形的性质与判定
【例2】(2017·宁夏)在边长为2的等边三角形ABC中，P是BC边上任意一点，过点 P分别作 PM⊥AB，PN⊥AC，M，N分别为垂足．(1)求证：不论点P在BC边的何处时都有PM＋PN的长恰好等于三角形ABC一边上的高；(2)当BP的长为何值时，四边形AMPN的面积最大，并求出最大值．
【对应训练2】(2017·恩施州)如图，△ABC，△CDE均为等边三角形，连接AD，BE交于点O，BE与AC交于点P.求证：∠AOB＝60°.
等腰三角形的情况考虑不全面．
【例3】(1)已知等腰三角形的一个内角为50°，则这个等腰三角形的顶角为( )A．50° B．80°C．50°或80° D．40°或65°
(2)(2016·河北)如图，∠AOB＝120°，OP平分∠AOB，且OP＝2.若点M，N分别在OA，OB上，且△PMN为等边三角形，则满足上述条件的△PMN有( )A．1个B．2个C．3个D．3个以上
30°或150°或90°
1．(2017·烟台)某城市几条道路的位置关系如图所示，已知AB∥CD，AE与AB的夹角为48°，若CF与EF的长度相等，则∠C的度数为( )A．48°B．40°C．30°D．24°
2．(2017·包头)若等腰三角形的周长为10 cm，其中一边长为2 cm，则该等腰三角形的底边长为（ ）A．2 cm B．4 cm C．6 cm D．8 cm
3．如图，在等边三角形ABC中，D是AC边上的中点，延长BC到点E，使CE＝CD，则∠E的度数为( )A．15° B．20° C．30° D．40°
5．(2017·益阳)如图，在△ABC中，AB＝AC，∠BAC＝36°，DE是线段AC的垂直平分线，若BE＝a，AE＝b，则用含a，b的代数式表示△ABC的周长为_________.
6．(2017·海南)已知△ABC的三边长分别为4，4，6，在△ABC所在平面内画一条直线，将△ABC分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画( ).A．3条 B．4条 C．5条 D．6
7．如图，在△ABC中，D为BC的中点，AD⊥BC，E为AD上一点，∠ABC＝60°，∠ECD＝40°，则∠ABE＝( )A．10° B．15° C．20° D．25°
9．如图，△ABC是等边三角形，点P是三角形内的任意一点，PD∥AB，PE∥BC，PF∥AC，若△ABC的周长为12，则PD＋PE＋PF＝___.
10．(2017·江西)如图①是一把园林剪刀，把它抽象为图②，其中OA＝OB.若剪刀张开的角为30°，则∠A＝____度．
11．(2017·内江)如图，AD平分∠BAC，AD⊥BD，垂足为点D，DE∥AC.求证：△BDE是等腰三角形．
证明：∵DE∥AC，∴∠1＝∠3，∵AD平分∠BAC，∴∠1＝∠2，∴∠2＝∠3，∵AD⊥BD，∴∠2＋∠B＝90°，∠3＋∠BDE＝90°，∴∠B＝∠BDE，∴△BDE是等腰三角形．
12．(2017·河池)已知等边△ABC的边长为12，D是AB上的动点，过D作DE⊥AC于点E，过E作EF⊥BC于点F，过F作FG⊥AB于点G.当G与D重合时，AD的长是( )A．3 B．4 C．8 D．9
13．如图，在△ABC中，AB＝AC，D，E两点分别在AC，BC上，BD是∠ABC的平分线，DE∥AB，若BE＝5 cm，CE＝3 cm，则△CDE的周长是( )A．15 cm B．13 cmC．11 cm D．9 cm
14．(2016·黔南州)如图，在△ABC中，∠C＝90°，∠B＝30°，AB的垂直平分线ED交AB于点E，交BC于点D，若CD＝3，则BD的长为____.
16．(2017·北京)如图，在△ABC中，AB＝AC，∠A＝36°，BD平分∠ABC交AC于点D.求证：AD＝BC.
证明：∵AB＝AC，∠A＝36°，∴∠ABC＝C＝72°，∵BD平分∠ABC交AC于点D，∴∠ABD＝∠DBC＝36°，∠BDC＝72°，∴∠A＝∠ABD，∠BDC＝∠C，∴AD＝BD＝BC.
17．(2017·连云港)如图，已知等腰三角形ABC中，AB＝AC，点D，E分别在边AB，AC上，且AD＝AE，连接BE，CD，交于点F.(1)判断∠ABE与∠ACD的数量关系，并说明理由；(2)求证：过点A，F的直线垂直平分线段BC.
解：(1)∠ABE＝∠ACD.理由：易证△ABE≌△ACD.∴∠ABE＝∠ACD.(2)证明：∵AB＝AC，∴∠ABC＝∠ACB.由(1)可知∠ABE＝∠ACD，∴∠FBC＝∠FCB.∴FB＝FC.∵AB＝AC，∴点A，F均在线段BC的垂直平分线上，即直线AF垂直平分线段BC.
18．(导学号65244098)如图，点A，B，C在一条直线上，△ABD，△BCE均为等边三角形，连接AE和CD，AE分别交CD，BD于点M，P，CD交BE于点Q，连接PQ，BM，下面结论：①△ABE≌△DBC；②∠DMA＝60°；③△BPQ为等边三角形；④MB平分∠AMC.其中结论正确的有( )A．1个 B．2个 C．3个 D．4个
19．(导学号65244099)如图，已知OB＝1，以OB为直角边作等腰直角三角形A1BO，再以OA1为直角边作等腰直角三角形A2A1O，如此下去，则线段OAn的长度为______.
20．(导学号65244100)(威海中考)操作发现：将一副直角三角板如图①摆放，能够发现等腰直角三角板ABC的斜边与含30°角的直角三角板DEF的长直角边DE重合．问题解决：将图①中的等腰直角三角板ABC绕点B顺时针旋转30°，点C落在BF上，AC与BD交于点O，连接CD，如图②.(1)求证：△CDO是等腰三角形；(2)若DF＝8，求AD的长．
解：(1)证明：由图①知BC＝DE，∴∠BDC＝∠BCD.∵∠DEF＝30°，∴∠BDC＝∠BCD＝75°.∵∠ACB＝45°，∴∠DCO＋∠BCO＝75°.∴∠DCO＝30°.∵∠DCO＋∠CDO＋∠DOC＝180°，∴∠DOC＝30°＋45°＝75°，∴∠DOC＝∠BDC，∴△CDO是等腰三角形．
21．(导学号65244101)(2017·呼和浩特)如图，等腰三角形ABC中，BD，CE分别是两腰上的中线．(1)求证：BD＝CE；(2)设BD与CE相交于点O，点M，N分别为线段BO和CO的中点，当△ABC的重心到顶点A的距离与底边长相等时，判断四边形DEMN的形状，无需说明理由．