2018届中考数学考点总复习课件：第19节　直角三角形与勾股定理 (共48张PPT)

这是一份2018届中考数学考点总复习课件：第19节　直角三角形与勾股定理 (共48张PPT)，共48页。PPT课件主要包含了直角三角形的性质，a2＋b2＝c2，直角三角形的判定，①②③④，－103等内容，欢迎下载使用。

1．直角三角形的两锐角______．2．勾股定理：如果直角三角形的两直角边长分别为a，b，斜边长为c，那么_______________.3．在直角三角形中，______上的中线等于斜边的一半．4．在直角三角形中，30°角所对的直角边是_______的一半．
5．有一个角是_____的三角形是直角三角形．6．有两个角_____的三角形是直角三角形．7．勾股定理的逆定理：如果三角形的三边长a，b，c满足a2＋b2＝c2，那么这个三角形是_______三角形．8．如果一个三角形一边上的______等于这边的一半，那么这个三角形是直角三角形.
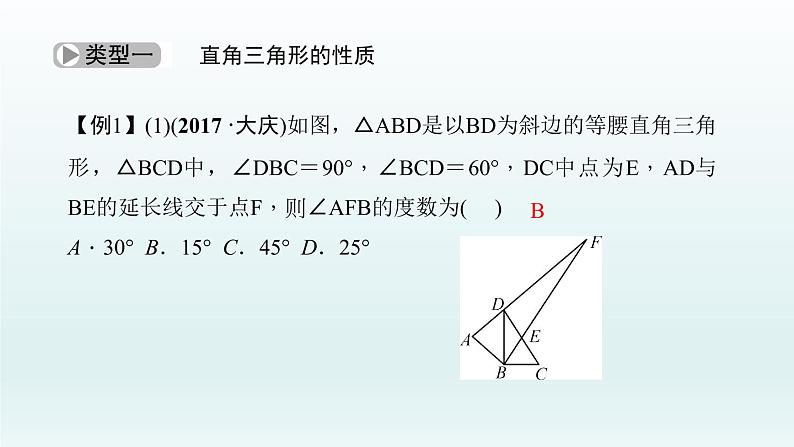
【例1】(1)(2017·大庆)如图，△ABD是以BD为斜边的等腰直角三角形，△BCD中，∠DBC＝90°，∠BCD＝60°，DC中点为E，AD与BE的延长线交于点F，则∠AFB的度数为( )A．30° B．15° C．45° D．25°
勾股定理及勾股定理的逆定理
(2)(2016·朝阳)如图，在平面直角坐标系中，矩形ABCO的边CO，OA分别在x轴、y轴上，点E在边BC上，将该矩形沿AE折叠，点B恰好落在边OC上的F处．若OA＝8，CF＝4，则点E的坐标是_________．
(3)(2017·黑龙江)如图，在△ABC中，AB＝BC＝8，AO＝BO，点M是射线CO上的一个动点，∠AOC＝60°，则当△ABM为直角三角形时，AM的长为______________.
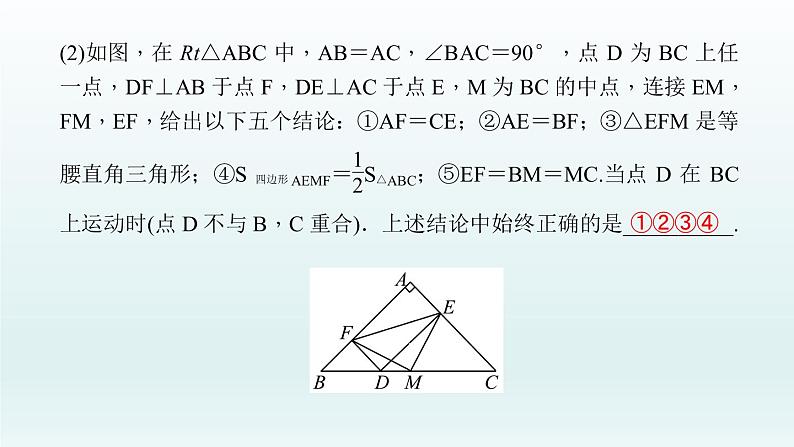
【思路引导】 (1)设AM＝2a，BM＝b.则正方形ABCD的面积＝4a2＋b2，由题意可知EF＝(2a－b)－2(a－b)＝2a－b－2a＋2b＝b，由此即可解决问题．(2)根据题意可以得到CE、OF的长度，根据点E在第二象限，从而可以得到点E的坐标．(3)分三种情况讨论：①当M在AB下方且∠AMB＝90°时，②当M在AB上方且∠AMB＝90°时，③当∠ABM＝90°时，分别根据含30°直角三角形的性质、直角三角形斜边的中线的性质或勾股定理，进行计算求解．
(2)(2017·襄阳)“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为a，较短直角边长为b，若(a＋b)2＝21，大正方形的面积为13，则小正方形的面积为( )A．3 B．4C．5 D．6
勾股定理及勾股定理的逆定理的应用
【例3】(1)(2017·绍兴)如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离为0.7 m，顶端距离地面2.4 m，如果保持梯子底端位置不动，将梯子斜靠在右墙时，顶端距离地面2 m，则小巷的宽度为( )A．0.7 m B．1.5 mC．2.2 m D．2.4 m
(2)(2017·东营)我国古代有这样一道数学问题：“枯木一根直立地上，高二丈，周三尺，有葛藤自根缠绕而上，五周而达其顶，问葛藤之长几何？”题意是：如图所示，把枯木看作一个圆柱体，因一丈是十尺，则该圆柱的高为20尺，底面周长为3尺，有葛藤自点A处缠绕而上，绕五周后其末端恰好到达点B处，则问题中葛藤的最短长度是___尺．
【思路引导】(1)根据勾股定理可求出梯子的长，进而求出梯子底端到右墙角的距离．(2)这种立体图形求最短路径问题，可以展开成为平面内的问题解决，展开后图形为直角三角形，所以是个直角三角形求斜边的问题，根据勾股定理可求出．
对直角三角形的第三边是斜边还是直角边的情况考虑不周全．
1．(2017·长沙)一个三角形的三个内角的度数之比为1∶2∶3，则这个三角形一定是( )A．锐角三角形 B．直角三角形C．钝角三角形 D．等腰直角三角形
2．如图，一个矩形纸片，剪去部分后得到一个三角形，则图中∠1＋∠2的度数是( )A．30° B．60°C．90° D．120°
3．(2016·南京)下列长度的三条线段能组成钝角三角形的是( )A．3，4，4 B．3，4，5 C．3，4，6 D．3，4，7
4．(2017·荆州)《九章算术》中的“折竹抵地”问题：今有竹高一丈，末折抵地，去根六尺．问折高者几何？意思是：一根竹子，原高一丈(一丈＝10尺)，一阵风将竹子折断，其竹梢恰好抵地，抵地处离竹子底部6尺远，问折断处离地面的高度是多少？设折断处离地面的高度为x尺，则可列方程为( )A．x2－6＝(10－x)2 B．x2－62＝(10－x)2C．x2＋6＝(10－x)2 D．x2＋62＝(10－x)2
5．(2017·株洲)如图，在△ABC中，∠B＝_______.
6．(2017·益阳)如图，△ABC中，AC＝5，BC＝12，AB＝13，CD是AB边上的中线．则CD＝_____.
7．(2017·安顺)三角形三边长分别为3，4，5，那么最长边上的中线长等于_____.
8．(2017·乐山)点A，B，C在格点图中的位置如图所示，格点小正方形的边长为1，则点C到线段AB所在直线的距离是______.
9．如图，在△ABC中，D为AC边的中点，且DB⊥BC，BC＝4，CD＝5.(1)求DB的长；(2)在△ABC中，求BC边上高的长．
10．直角三角形的一个锐角是另一个锐角的4倍，那么这个锐角的度数是( )A．18° B．36° C．54° D．72°
14．(导学号65244102)(2017·青岛)如图，在四边形ABCD中，∠ABC＝∠ADC＝90°，E为对角线AC的中点，连接BE，ED，BD.若∠BAD＝58°，则∠EBD的度数为____度．
16．勾股定理是一条古老的数学定理，它有很多种证明方法．我国汉代数学家赵爽根据弦图，利用面积进行了证明．著名数学家华罗庚提出把“数形关系”(勾股定理)带到其他星球，作为地球人与其他星球“人”进行第一次“谈话”的语言．(1)请根据图①中直角三角形叙述勾股定理；
19．(导学号65244105)如图，有两条公路OM，ON相交成30°角，沿公路OM方向离O点80 m处有一所学校A.当重型运输卡车P沿道路ON方向行驶时，在以P为圆心50 m长为半径的圆形区域内都会受到卡车噪声的影响，且卡车P与学校A的距离越近噪声影响越大．若已知重型运输卡车P沿道路ON方向行驶的速度为18 km/h.(1)求对学校A的噪声影响最大时卡车P与学校A的距离；(2)求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间．
解：(1)过点A作AD⊥ON于点D，∵∠NOM＝30°，AO＝80 m，∴AD＝40 m，即对学校A的噪声影响最大时卡车P与学校A的距离为40 m.
20．(导学号65244106)如图，在Rt△ABC中，∠B＝90°，AC＝60 cm，∠A＝60°，点D从点C出发沿CA方向以4 cm/s的速度向点A匀速运动，同时点E从点A出发沿AB方向以2 cm/s的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t s(0＜t≤15)．过点D作DF⊥BC于点F，连接DE，EF.(1)求证：AE＝DF；(2)四边形AEFD能够成为菱形吗？如果能，求出相应的t值，如果不能，说明理由；(3)当t为何值时，△DEF为直角三角形？请说明理由．