





2018届中考数学考点总复习课件:第20节 锐角三角函数与解直角三角形 (共54张PPT)
展开锐角三角函数及特殊角的三角函数值
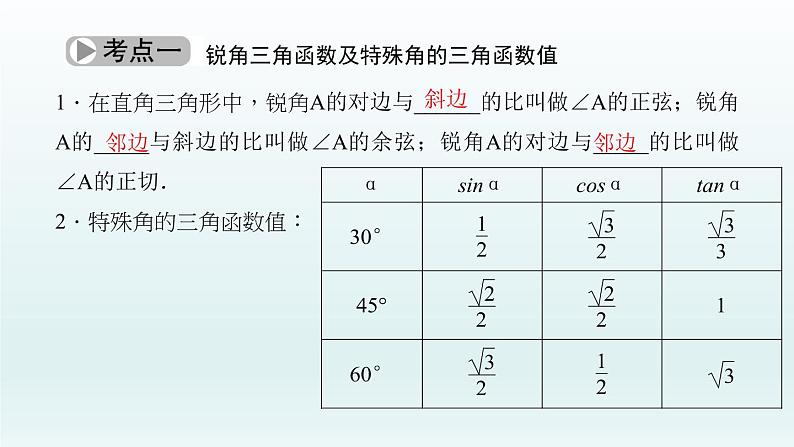
1.在直角三角形中,锐角A的对边与______的比叫做∠A的正弦;锐角A的_____与斜边的比叫做∠A的余弦;锐角A的对边与_____的比叫做∠A的正切.2.特殊角的三角函数值:
3.三角函数的增减性:当0°<α<90°时,sinα及tanα均随α的增大而 _____(或减小而____),csα随α的增大而 _____(或减小而______).
解直角三角形及其应用
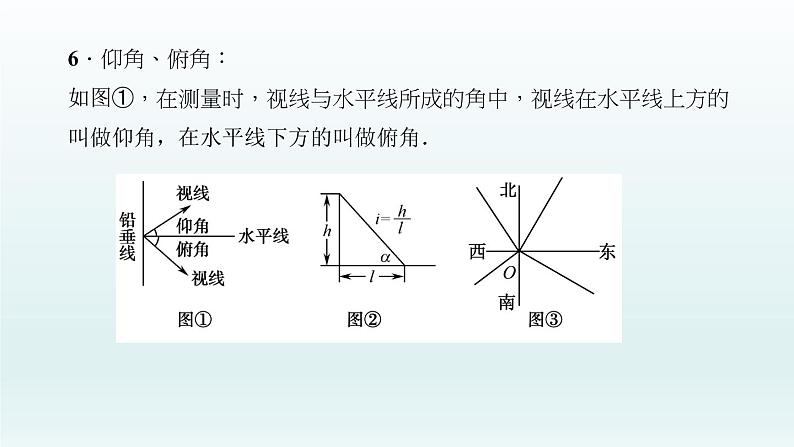
6.仰角、俯角:如图①,在测量时,视线与水平线所成的角中,视线在水平线上方的叫做仰角,在水平线下方的叫做俯角.
锐角三角函数及特殊的三角函数值
(2)(2017·无锡)在如图的正方形方格纸中,每个小的四边形都是相同的正方形,A,B,C,D都在格点处,AB与CD相交于点O,则tan∠BOD的值等于____.
【思路引导】(1)根据勾股定理求出BC,由正弦的概念进行计算.(2)根据平移的性质和锐角三角函数以及勾股定理,通过转化的数学思想可以求得tan∠BOD的值.
【例2】有一块三角形形状的花圃ABC,现可直接测得∠A=30°,AC=40 m,BC=25 m,请你求出这块花圃的边AB的长.【思路引导】注意∠B可能是锐角也可能是钝角,需分类讨论.
【例3】(1)(2017·白银)美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132 m,求观景亭D到南滨河路AC的距离约_____m .(结果精确到1米,参考数据:sin65°≈0.91,cs65°≈0.42,tan65°≈2.14)
(2)(2017·随州)风电已成为我国继煤电、水电之后的第三大电源,风电机组主要由塔杆和叶片组成(如图①),图②是从图①引出的平面图.假设你站在A处测得塔杆顶端C的仰角是55°,沿HA方向水平前进43 m到达山底G处,在山顶B处发现正好一叶片到达最高位置,此时测得叶片的顶端D(D,C,H在同一直线上)的仰角是45°.已知叶片的长度为35 m(塔杆与叶片连接处的长度忽略不计),山高BG为10 m,BG⊥HG,CH⊥AH,则塔杆CH=____m.(参考数据:tan55°≈1.4,tan35°≈0.7,sin55°≈0.8,sin35°≈0.6)
(3)(2017·海南)为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供的方案是:水坝加高2 m(即CD=2 m),背水坡DE的坡度i=1∶1(即DB∶EB=1∶1),如图所示,已知AE=4 m,∠EAC=130°,求水坝原来的高度BC.(参考数据:sin50°≈0.77,cs50°≈0.64,tan50°≈1.2)
【思路引导】设BC=x m,用x表示出AB的长,利用坡度的定义得到BD=BE,进而列出x的方程,求出x的值即可.
没有分锐角三角形或钝角三角形讨论而出错.
7.(2017·大庆)如图,已知一条东西走向的河流,在河流对岸有一点A,小明在岸边点B处测得点A在点B的北偏东30°方向上,小明沿河岸向东走80 m后到达点C,测得点A在点C的北偏西60°方向上,则点A到河岸BC的距离为_______m.
9.(2017·宜昌)△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列选项中,错误的是( )A.sinα=csα B.tanC=2C.sinβ=csβ D.tanα=1
12.(2016·娄底)如图,已知在Rt△ABC中,∠ABC=90°,点D沿BC自B向C运动(点D与点B,C不重合),作BE⊥AD于点E,CF⊥AD于点F,则BE+CF的值( )A.不变 B.增大C.减小 D.先变大再变小
13.(2017·兰州)如图,一个斜坡长130 m,坡顶离水平地面的距离为50 m,那么这个斜坡与水平地面夹角的正切值等于______.
15.(导学号65244107)(2017·百色)如图,在距离铁轨200 m的B处,观察由南宁开往百色的“和谐号”动车,当动车车头在A处时,恰好位于B处的北偏东60°方向上;10 s后,动车车头到达C处,恰好位于B处的西北方向上,则这时段动车的平均速度是____________m/s.
16.(2016·丽水)数学拓展课程《玩转学具》课堂中,小陆同学发现:一副三角板中,含45°的三角板的斜边与含30°的三角板的长直角边相等,于是,小陆同学提出一个问题:如图,将一副三角板直角顶点重合拼放在一起,点B,C,E在同一直线上,若BC=2,求AF的长.请你运用所学的数学知识解决这个问题.
18.(导学号65244108)(2017·重庆)如图,已知点C与某建筑物底端B相距306 m(点C与点B在同一水平面上),某同学从点C出发,沿同一剖面的斜坡CD行走195 m至坡顶D处,斜坡CD的坡度(或坡比)i=1∶2.4,在D处测得该建筑物顶端A的俯视角为20°,则建筑物AB的高度约为(精确到0.1 m,参考数据:sin20°≈0.342,cs20°≈0.940,tan20°≈0.364) ( ) A.29.1 m B.31.9 mC.45.9 m D.95.9 m
19.(导学号65244109)(2017·杭州)如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( )A.x-y2=3 B.2x-y2=9C.3x-y2=15 D.4x-y2=21
22.(导学号65244112)(2017·鄂州)小明想要测量学校食堂和食堂正前方一棵树的高度,他从食堂楼底M处出发,向前走3 m到达A处,测得树顶端E的仰角为30°,他又继续走下台阶到达C处,测得树的顶端E的仰角是60°,再继续向前走到大树底D处,测得食堂楼顶N的仰角为45°.已知A点离地面的高度AB=2 m,∠BCA=30°,且B,C,D三点在同一直线上.(1)求树DE的高度;(2)求食堂MN的高度.
2018届中考数学考点总复习课件:第23节 圆的有关性质 (共54张PPT): 这是一份2018届中考数学考点总复习课件:第23节 圆的有关性质 (共54张PPT),共54页。PPT课件主要包含了半圆劣弧,同心圆,两条弧,垂直于,弦圆心角,圆心角,圆周角,垂径定理及推论,圆周角定理及推论,°或105°等内容,欢迎下载使用。
2018届中考数学考点总复习课件:第4节 分 式 (共26张PPT): 这是一份2018届中考数学考点总复习课件:第4节 分 式 (共26张PPT),共26页。PPT课件主要包含了B≠0,B=0,A=0且B≠0,公因式,基本性质,同分母,最简公分母,x-1,分式的基本性质用错等内容,欢迎下载使用。
2018届中考数学考点总复习课件:第29节 投影与视图 (共40张PPT): 这是一份2018届中考数学考点总复习课件:第29节 投影与视图 (共40张PPT),共40页。PPT课件主要包含了垂直于,三视图,主视图,俯视图,左视图,+15π等内容,欢迎下载使用。












