2018届中考数学专题复习课件：专题十　与几何图形有关的探究题 (共38张PPT)

这是一份2018届中考数学专题复习课件：专题十　与几何图形有关的探究题 (共38张PPT)，共38页。

本题型基本上是每年中考的必考题，且多以几何压轴题的形式出现，常把圆、四边形与三角函数的知识结合起来考查，综合程度较高，所以难度较大．预计2018年仍会考查与几何图形有关的探究题．
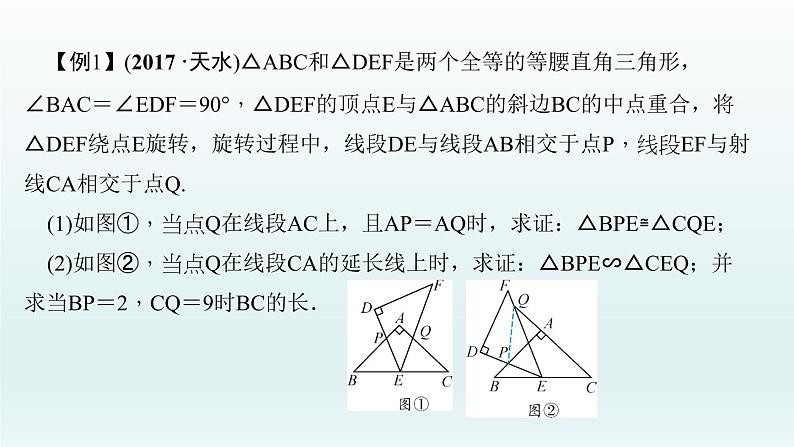
【例1】(2017·天水)△ABC和△DEF是两个全等的等腰直角三角形，∠BAC＝∠EDF＝90°，△DEF的顶点E与△ABC的斜边BC的中点重合，将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q.(1)如图①，当点Q在线段AC上，且AP＝AQ时，求证：△BPE≌△CQE；(2)如图②，当点Q在线段CA的延长线上时，求证：△BPE∽△CEQ；并求当BP＝2，CQ＝9时BC的长．
【思路引导】(1)由△ABC是等腰直角三角形，得∠B＝∠C＝45°，AB＝AC，又由AP＝AQ，E是BC的中点，利用SAS，可证得△BPE≌△CQE.(2)由已知，易得∠B＝∠C＝∠DEF＝45°，然后利用三角形的外角的性质，即可得∠BEP＝∠EQC，从而可证得△BPE∽△CEQ；再根据相似三角形的对应边成比例，从而可求得BE的长，由此可得BC的长．
【例2】(2017·东营)如图，在等腰三角形ABC中，∠BAC＝120°，AB＝AC＝2，点D是BC边上的一个动点(不与B，C重合)，在AC上取一点E，使∠ADE＝30°.(1)求证：△ABD∽△DCE；
【思路引导】根据已知条件找到两组对应角相等，从而证明△ABD∽△DCE.
证明：∵△ABC是等腰三角形，且∠BAC＝120°，∴∠ABD＝∠ACB＝30°.∴∠ABD＝∠ADE＝30°.∵∠ADC＝∠ADE＋∠EDC＝∠ABD＋∠DAB，∴∠EDC＝∠DAB.∴△ABD∽△DCE.
(2)设BD＝x，AE＝y，求y关于x的函数解析式，并写出自变量x的取值范围；【思路引导】如图，作高AF，根据含30 °角的直角三角形的性质求AF的长，根据勾股定理求BF的长，则可得BC的长，根据(1)中的相似三角形列比例式可得函数解析式，并确定自变量的取值范围．
2．(导学号65244268)(2017·天门)在Rt△ABC中，∠ACB＝90°，点D与点B在AC同侧，∠DAC＞∠BAC，且DA＝DC，过点B作BE∥DA交DC于点E，M为AB的中点，连接MD，ME.(1)如图①，当∠ADC＝90°时，线段MD与ME的数量关系是MD＝ME；(2)如图②，当∠ADC＝60°时，试探究线段MD与ME的数量关系，并证明你的结论；
3．(导学号65244269)(1)如图①，在平行四边形纸片ABCD中，AD＝5，S▱ABCD＝15，过点A作AE⊥BC，垂足为E，沿AE剪下△ABE，将它平移至△DCE′的位置，拼成四边形AEE′D，则四边形AEE′D的形状为 ．A．平行四边形 B．菱形C．矩形 D．正方形
(2)如图②，在(1)中的四边形纸片AEE′D中，在EE′上取一点F，使EF＝4，剪下△AEF，将它平移至△DE′F′的位置，拼成四边形AFF′D.①求证：四边形AFF′D是菱形．②求四边形AFF′D的两条对角线的长．
4．(导学号65244270)(2017·郴州)如图①，△ABC是边长为4 cm的等边三角形，边AB在射线OM上，且OA＝6 cm，点D从O点出发，沿OM的方向以1 cm/s的速度运动，当D不与点A重合时，将△ACD绕点C逆时针方向旋转60°得到△BCE，连接DE.(1)求证：△CDE是等边三角形；(2)如图②，当6＜t＜10时，△BDE的周长是否存在最小值？若存在，求出△BDE的最小周长；若不存在，请说明理由；(3)如图③，当点D在射线OM上运动时，是否存在以D，E，B为顶点的三角形是直角三角形？若存在，求出此时t的值；若不存在，请说明理由．
(3)存在．Ⅰ.∵当点D与点B重合时，D，B，E不能构成三角形，∴当点D与点B重合时，不符合题意；Ⅱ.当0≤t＜6时，由旋转可知，∠ABE＝60°，∠BDE＜60°，∴∠BED＝90°.由(1)可知，△CDE是等边三角形，∴∠DEC＝60°.∴∠CEB＝30°.∵∠CEB＝∠CDA，∴∠CDA＝30°.∵∠CAB＝60°，∴∠ACD＝∠ADC＝30°.∴DA＝CA＝4 cm.∴OD＝OA－DA＝6－4＝2 cm，∴t＝2÷1＝2；
Ⅲ.当6＜t＜10时，由∠DBE＝120°＞90°，∴此时不存在；Ⅳ.当t＞10时，由旋转的性质可知，∠DBE＝60°，又由(1)知∠CDE＝60°，∴∠BDE＝∠CDE＋∠BDC＝60°＋∠BDC.而∠BDC＞0°，∴∠BDE＞60°.∴只能∠BDE＝90°.从而∠BED＝∠BCD＝∠BDC＝30°.∴BD＝BC＝4 cm.∴OD＝14 cm，∴t＝14÷1＝14 s．综上所述：当t＝2或14时，以D，E，B为顶点的三角形是直角三角形．
5．(导学号65244271)(2017·淄博)如图，将矩形纸片ABCD沿直线MN折叠，顶点B恰好与CD边上的动点P重合(点P不与点C，D重合)，折痕为MN，点M，N分别在边AD，BC上，连接MB，MP，BP，BP与MN相交于点F.(1)求证：△BFN∽△BCP；(2)①在图2中，作出经过M，D，P三点的⊙O(要求保留作图痕迹，不写作法)；②设AB＝4，随着点P在CD上的运动，若①中的⊙O恰好与BM，BC同时相切，求此时DP的长．
解：(1)证明：∵将矩形纸片ABCD沿直线MN折叠，顶点B恰好与CD边上的动点P重合，∴MN垂直平分线段BP.∴∠BFN＝90°.∵四边形ABCD为矩形，∴∠C＝90°.∵∠FBN＝∠CBP，∴△BFN∽△BCP.(2)①在图甲中，作MD，DP的垂直平分线，交于点O，以OD为半径作圆即可，如图所示．