






2018届中考数学专题复习课件:专题五 统计与概率的应用 (共37张PPT)
展开在中考中,对统计单独进行考查较少,但概率为常考点,主要考查:①简单概率的计算;②用列表法或画树状图法计算概率;③面积法求概率.一般综合统计与概率的知识考查,常以解答题的形式出现,预计2018年中考仍会以此形式进行考查.
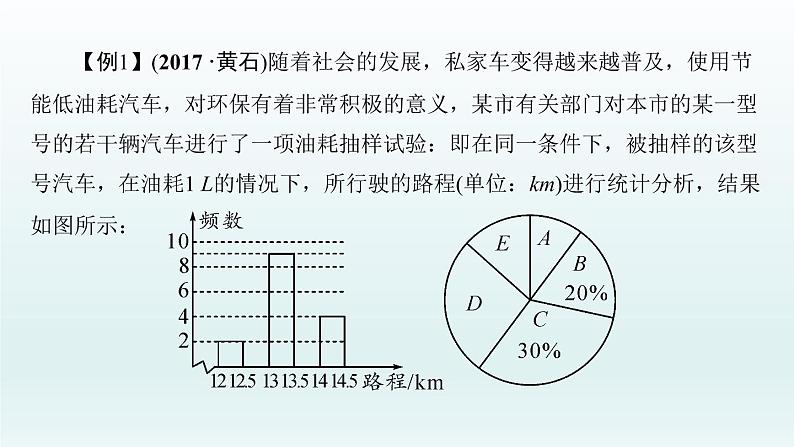
【例1】(2017·黄石)随着社会的发展,私家车变得越来越普及,使用节能低油耗汽车,对环保有着非常积极的意义,某市有关部门对本市的某一型号的若干辆汽车进行了一项油耗抽样试验:即在同一条件下,被抽样的该型号汽车,在油耗1 L的情况下,所行驶的路程(单位:km)进行统计分析,结果如图所示:
(注:记A为12~12.5,B为12.5~13,C为13~13.5,D为13.5~14,E为14~14.5)请依据统计结果回答以下问题:(1)试求进行该试验的车辆数;(2)请补全频数分布直方图;(3)若该市有这种型号的汽车约900辆(不考虑其他因素),请利用上述统计数据初步预测,该市约有多少辆该型号的汽车,在耗油1 L的情况下可以行驶13 km以上?
【思路引导】(1)根据C所占的百分比以及频数,即可得到进行该试验的车辆数.(2)根据B的百分比,计算得到B的频数,进而得到D的频数,据此补全频数分布直方图.(3)根据C,D,E所占的百分比之和乘该市这种型号的汽车的总数,即可得到结果.
解:(1)进行该试验的车辆数为:9÷30%=30(辆).(2)B:20%×30=6(辆),D:30-2-6-9-4=9(辆),补全频数分布直方图如下:
【例2】(2017·湘潭)从-2,1,3这三个数中任取两个不同的数,作为点的坐标.(1)写出该点所有可能的坐标;(2)求该点在第一象限的概率.【思路引导】(1)首先根据题意画出树状图,然后由树状图可得所有等可能的结果.(2)由(1)得出点刚好落在第一象限的情况,由概率公式即可求出问题答案.
解:(1)画树状图得:
∴所有可能的坐标为(1,3),(1,-2),(3,1),(3,-2),(-2,1),(-2,3).
【例3】(2017·十堰)某中学艺术节期间,学校向学生征集书画作品,杨老师从全校30个班中随机抽取了4个班(用A,B,C,D表示),对征集到的作品的数量进行了分析统计,制作了两幅不完整的统计图.请根据以上信息,回答下列问题:(1)杨老师采用的调查方式是 (填“普查”或“抽样调查”);(2)请你将条形统计图补充完整,并估计全校共征集多少件作品;
(3)如果全校征集的作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生,现要在获得一等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求恰好选取的两名学生性别相同的概率.解:画树状图得:
1.(2017·武汉)某公司共有A,B,C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图:各部门人数及每人所创年利润统计表
(1)①在扇形图中,C部门所对应的圆心角的度数为 ;②在统计表中,b=__,c=___;(2)求这个公司平均每人所创年利润.
2.(2017·大庆)某校为了解学生平均每天课外阅读的时间,随机调查了该校部分学生一周内平均每天课外阅读的时间(以分钟为单位,并取整数),将有关数据统计整理并绘制成尚未完成的频率分布表和频数分布直方图.请你根据图表中所提供的信息,解答下列问题.
(注:这里的15~25表示大于等于15同时小于25)(1)求被调查的学生人数;(2)直接写出频率分布表中的a和b的值,并补全频数分布直方图;(3)若该校共有学生500名,则平均每天课外阅读的时间不少于35分钟的学生大约有多少名?
(3)平均每天课外阅读的时间不少于35分钟的学生大约有500×(0.40+0.12+0.10)=310(人).
3.(导学号65244240)(2017·宜昌)宜昌市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够,导致出现需要租用却未租到车的现象,现随机抽取的某五天在同一时段的调查数据汇成如下表格:
请回答下列问题:(1)表格中的五个数据(人数)的中位数是多少?(2)由随机抽样估计,平均每天在7:00~8:00需要租用公共自行车的人数是多少?
解:(1)表格中5个数据按从小到大的顺序排列为1 200,1 200,1 300,1 300,1 500,所以中位数是1 300.(2)平均每天需要租用自行车却未租到车的人数:(1 500+1 200+1 300+1 300+1 200)÷5=1 300(人),∵宜昌市首批一次性投放公共自行车700辆供市民租用出行,∴平均每天需要租用公共自行车的人数是1 300+700=2 000(人).
4.市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表:
(1)把表中所空各项数据填写完整;(2)分别计算甲、乙六次测试成绩的方差;(3)根据(1)(2)计算的结果,你认为推荐谁参加省比赛更合适?请说明理由.
(3)推荐甲参加省比赛更合适,理由如下:两人的平均成绩相等,说明实力相当;但甲的六次测试成绩的方差比乙小,说明甲发挥较为稳定,故推荐甲参加比赛更合适.
5.(2017·鄂州)某兴趣小组为了了解本校学生参加课外体育锻炼情况,随机抽取本校40名学生进行问卷调查,统计整理并绘制了如下两幅尚不完整的统计图:根据以上信息解答下列问题:
(1)课外体育锻炼情况扇形统计图中,“经常参加”所对应的圆心角的度数为 ;经常参加课外体育锻炼的学生最喜欢的一种项目条形统计图中,喜欢足球的人数有1人,补全条形统计图;(2)该校共有1 200名学生,请估计全校学生中经常参加课外体育锻炼并喜欢的项目是乒乓球的人数有多少人;(3)若在“乒乓球”、“篮球”、“足球”、“羽毛球”项目中任选两个项目成立兴趣小组,请用列表法或画树状图的方法求恰好选中“乒乓球”、“篮球”这两个项目的概率.
解:(1)补全统计图如图所示:
6.(导学号65244241)(2017·毕节)由于只有1张市运动会开幕式的门票,小王和小张都想去,两人商量采取转转盘(如图,转盘盘面被分为面积相等,且标有数字1,2,3,4的4个扇形区域)的游戏方式决定谁胜谁去观看.规则如下:两人各转动转盘一次,当转盘指针停止,如两次指针对应盘面数字都是奇数,则小王胜;如两次指针对应盘面数字都是偶数,则小张胜;如两次指针对应盘面数字是一奇一偶,视为平局.若为平局,继续上述游戏,直至分出胜负.如果小王和小张按上述规则各转动转盘一次,求:(1)小王转动转盘,当转盘指针停止,对应盘面数字为奇数的概率是多少?(2)该游戏是否公平?请用列表或画树状图的方法说明理由.
7.(导学号65244242)(2017·呼和浩特)为了解某地某个季度的气温情况,用适当的抽样方法从该地这个季度中抽取30天,对每天的最高气温x(单位:℃)进行调查,并将所得的数据按照12≤x<16,16≤x<20,20≤x<24,24≤x<28,28≤x<32分成五组,得到如图频数分布直方图.(1)求这30天最高气温的平均数和中位数(各组的实际数据用该组的组中值代表);(2)每月按30天计算,各组的实际数据用该组的组中值代表,估计该地这个季度中最高气温超过(1)中平均数的天数;(3)如果从最高气温不低于24 ℃的两组内随机选取两天,请你直接写出这两天都在气温最高一组内的概率.
8.(导学号65244243)(2017·连云港)为落实“垃圾分类”,环卫部门要求垃圾要按A,B,C三类分别装袋、投放,其中A类指废电池、过期药品等有毒垃圾,B类指剩余食品等厨房垃圾,C类指塑料、废纸等可回收垃圾.甲投放了一袋垃圾,乙投放了两袋垃圾,这两袋垃圾不同类.(1)直接写出甲投放的垃圾恰好是A类的概率;(2)求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.
中考数学复习第十一章解答题突破(二)第40课时统计与概率的应用课件: 这是一份中考数学复习第十一章解答题突破(二)第40课时统计与概率的应用课件,共25页。PPT课件主要包含了数据分析表等内容,欢迎下载使用。
初中数学中考复习 专题五 动态问题课件PPT: 这是一份初中数学中考复习 专题五 动态问题课件PPT,共5页。
2018年中考数学总复习课件:专题五、六 计算专题、应用题专题 (共15张PPT): 这是一份2018年中考数学总复习课件:专题五、六 计算专题、应用题专题 (共15张PPT),共15页。PPT课件主要包含了专题六应用题专题等内容,欢迎下载使用。












