






高中数学人教版新课标A必修31.3 算法与案例备课ppt课件
展开计算机程序(程序语言)
[问题1]:在小学,我们已经学过求最大公约数的知识,你能求出18与90的最大公约数吗?
∴18和90的最大公约数是2×3×3=18.
辗转相除法(欧几里得算法)
观察用辗转相除法求8251和6105的最大公约数的过程
第一步 用两数中较大的数除以较小的数,求得商和余数8251=6105×1+2146
结论:8251和6105的公约数就是6105和2146的公约数,求8251和6105的最大公约数,只要求出6105和2146的公约数就可以了。
第二步 对6105和2146重复第一步的做法6105=2146×2+1813同理6105和2146的最大公约数也是2146和1813的最大公约数。
思考:从上述的过程你体会到了什么?思考:从上述的过程你体会到了什么?
8251=6105×1+2146
6105=2146×2+1813
2146=1813×1+333
1813=333×5+148
333=148×2+37
例2 用辗转相除法求225和135的最大公约数
225=135×1+90
135=90×1+45
显然37是148和37的最大公约数,也就是8251和6105的最大公约数
显然45是90和45的最大公约数,也就是225和135的最大公约数
思考1:从上面的两个例子可以看出计算的规律是什么?
1、辗转相除法(欧几里得算法)
(1)算理:所谓辗转相除法,就是对于给定的两个数,用较大的数除以较小的数。若余数不为零,则将余数和较小的数构成新的一对数,继续上面的除法,直到大数被小数除尽,则这时较小的数就是原来两个数的最大公约数。
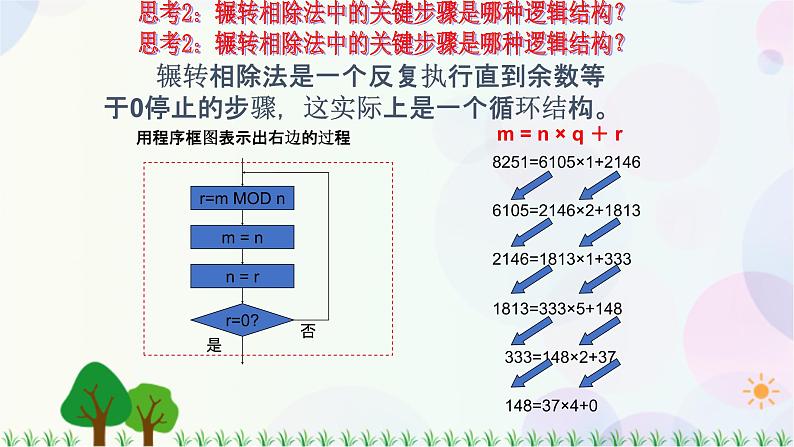
辗转相除法是一个反复执行直到余数等于0停止的步骤,这实际上是一个循环结构。
m = n × q + r
用程序框图表示出右边的过程
思考2:辗转相除法中的关键步骤是哪种逻辑结构? 思考2:辗转相除法中的关键步骤是哪种逻辑结构?
第一步:输入两个正整数m,n(m>n).第二步:计算m除以n所得的余数r.第三步:m=n,n=r.第四步:若r=0,则m,n的最大公约数等于m; 否则转到第二步. 第五步:输出最大公约数m.
INPUT“m,n=“;m,nDO r=m MOD n m=n n=rLOOP UNTIL r=0PRINT mEND
1.所谓辗转相除法定义 就是对于给定的两个数,用较大的数除以较小的数。若余数不为零,则将除数变被除数,余数变除数,继续上面的除法,直到大数被小数除尽,则这时最后的除数就是原来两个数的最大公约数。
辗转相除法是一个反复执行直到余数等于0停止的算法
2.辗转相除法求最大公约数算法步骤第一步,给定两个正数m,n第二步,计算m除以n所得到余数r第三步,m=n,n=r第四步,若r=0,则m,n的最大公约数等于m; 否则,返回第二步
LOOP UNTIL r=0
3辗转相除法的程序框图
问题3.介绍我国《九章算术》中的更相减损术
算理:可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也,以等数约之。
第一步:任意给定两个正整数;判断他们是否都是偶数。若是,则用2约简;若不是则执行第二步。
第二步:以较大的数减较小的数,接着把所得的差与较小的数比较,并以大数减小数。继续这个操作,直到所得的减数和差相等为止,则这个等数就是所求的最大公约数。
例2用更相减损术求98与63的最大公约数.
解:由于63不是偶数,把98和63以大数减小数,并辗转相减,
即:98-63=35; 63-35=28; 35-28=7; 28-7=21; 21-7=14; 14-7=7.
所以,98与63的最大公约数是7。
例3 用更相减损术求98与63的最大公约数
解:由于63不是偶数,把98和63以大数减小数,并辗转相减
98-63=35 63-35=28 35-28=7 28-7=2121-7=2114-7=7
所以,98和63的最大公约数等于7
第一步:输入两个正整数a,b(a>b);第二步:若a不等于b ,则执行第三步;否则转到第五步;第三步:把a-b的差赋予r;第四步:如果b>r, 那么把b赋给a,把r赋给b;否则把r赋给a,执行第二步;第五步:输出最大公约数b.
INPUT “a,b=“;a,bWHILE a<>b r=a-b IF b>r THEN a=b b=r ELSE a=r END IFWENDPRINT bEND
1.所谓更相减损术定义 就是对于给定的两个数,用较大的数减去较小的数,然后将差和较小的数构成新的一对数,再用较大的数减去较小的数,反复执行此步骤直到差数和较小的数相等,此时相等的两数便为原来两个数的最大公约数。
2.辗转相除法与更相减损术的比较(1)都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主;计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显。(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损术则以减数与差相等而得到.
秦九韶算法 秦九韶算法
1、求两个数的最大公约数的两种方法分别是( )和( )。2、两个数21672,8127的最大公约数是 ( )A、2709 B、2606 C、2703 D、2706
怎样求多项式f(x)=x5+x4+x3+x2+x+1当x=5时的值呢?
共做了1+2+3+4=10次乘法运算,5次加法运算
共做了4次乘法运算,5次加法运算。
《数书九章》——秦九韶算法
对该多项式按下面的方式进行改写:
思考:当知道了x的值后该如何求多项式的值?思考:当知道了x的值后该如何求多项式的值?
这是怎样的一种改写方式?最后的结果是什么?
要求多项式的值,应该先算最内层的一次多项式的值,即
然后,由内到外逐层计算一次多项式的值,即
这种将求一个n次多项式f(x)的值转化成求n个一次多项式的值的方法,称为秦九韶算法。
思考:在求多项式的值上,这是怎样的一个转化?思考:在求多项式的值上,这是怎样的一个转化?
第一步:输入多项式次数n、最高次项的系数an和x的值.
第二步:将v的值初始化为an,将i的值初始化为1.
第三步:输入i次项的系数an-i.
第四步:v=vx+an-i,i=i+1.
第五步:判断i是否小于或等于n,若是,则返回第三步;否则,输出多项式的值v。
这是一个在秦九韶算法中反复执行的步骤,因此可用循环结构来实现。
特点:通过一次式的反复计算,逐步得出高次多项式的值,对于一个n次多项式,只需做n次乘法和n次加法即可。
例2 已知一个五次多项式为
用秦九韶算法求这个多项式当x = 5的值。
按由里到外的顺序,依此计算一次多项式当x = 5时的值:
所以,当x = 5时,多项式的值等于17255.2
你从中看到了怎样的规律?怎么用程序框图来描述呢?
练习、已知多项式f(x)=x5+5x4+10x3+10x2+5x+1用秦九韶算法求这个多项式当x=-2时的值的过程中,求
2、最常见的进位制是什么?除此之外还有哪些常见的进位制?请举例说明.
进位制是人们为了计数和运算方便而约定的记数系统。
进位制是一种记数方式,用有限的数字在不同的位置表示不同的数值。可使用数字符号的个数称为基数,基数为n,即可称n进位制,简称n进制。
我们常见的数字都是十进制的,比如一般的数值计算,但是并不是生活中的每一种数字都是十进制的.古人有半斤八两之说,就是十六进制与十进制的转换.比如时间和角度的单位用六十进位制, 计算“一打”数值时是12进制的。电子计算机用的是二进制
3、我们了解十进制吗?所谓的十进制,它是如何构成的?
其它进位制的数又是如何的呢?
(用10个数字来记数,称基数为10)
二进制是用0、1两个数字来描述的.如11001
区分的写法:11001(2)或者(11001)2
anan-1an-2…a1(k)?
三、二进制与十进制的转换
1、二进制数转化为十进制数
例1 将二进制数110011(2)化成十进制数
所以,110011(2)=51.
注意:1.最后一步商为0,2.将上式各步所得的余数从下到上排列,得到: 89=1011001(2)
2、十进制转换为二进制
例2 把89化为二进制数
例3 把89化为五进制数
3、十进制转换为其它进制
以5作为除数,相应的除法算式为:
所以,89=324(5)
练习:完成下列进位制之间的转化:(1)10231(4)= (10);(2)235(7)= (10);(3)137(10)= (6);(4)1231(5)= (7);(5)213(4)= (3);(6)1010111(2)= (4)。
1.进位制是一种记数方式,用有限的数字在不同的位置表示不同的数值。可使用数字符号的个数称为基数,基数为k,即可称k进位制,简称k进制。k进制需要使用k个数字;
2.十进制与二进制之间转换的方法; 先把这个k进制数写成用各位上的数字与k的幂的乘积之和的形式,再按照十进制数的运算规则计算出结果。
人教版新课标A必修33.1.2概率的意义备课ppt课件: 这是一份人教版新课标A必修33.1.2概率的意义备课ppt课件,共31页。PPT课件主要包含了概率的正确理解,游戏的公平性,这样的游戏公平吗等内容,欢迎下载使用。
人教版新课标A1.2.3循环语句备课课件ppt: 这是一份人教版新课标A1.2.3循环语句备课课件ppt,共23页。PPT课件主要包含了选出该城市,有一城市得过半票,淘汰得票最少者,当型循环,直到型循环,循环体,Next,i50,ii+1,f10f21等内容,欢迎下载使用。
高中数学人教版新课标A必修3第三章 概率3.2 古典概型3.2.1古典概型备课课件ppt: 这是一份高中数学人教版新课标A必修3第三章 概率3.2 古典概型3.2.1古典概型备课课件ppt,共31页。PPT课件主要包含了考察两个试验,基本事件有什么特点,树状图,问题2,有限性,等可能性,古典概型,抽象概括,古典的概率模型,思考交流等内容,欢迎下载使用。













