小学数学北师大版六年级下册总复习数与代数复习课件ppt

这是一份小学数学北师大版六年级下册总复习数与代数复习课件ppt，共21页。PPT课件主要包含了2列数量关系式，可以列表，可以画图，5千米，答要6小时完成，答能做70根跳绳等内容，欢迎下载使用。
1.使学生进一步理解比的意义和基本性质以及比、分数与除法的关系；理解比的基本性质与分数的基本性质、商不变的规律内在一致性；理解比例的意义和基本性质。 2.能运用比和比例的知识解决一些简单实际问题，丰富解决问题策略，积累解决问题的经验。3.通过一题多变、一题多解等形式，由浅入深，由易到难，培养学生思维的灵活性。
【重点】能运用比和比例的知识解决一些简单实际问题。
【难点】解决一题多变、一题多解等形式的实际问题。
用比例知识解决问题的步骤
(1)认真审题，判断哪两种量成什么比例。
(3)设未知数，列出等式并解答。
(4)检验结果是否正确。
如：某农场每天收割小麦60公顷，20天完成。如果每天收割80公顷，多少天可以完成？
解：设x 天可以完成。 80x =60×20 80x =1200 x =15 答：15天可以完成。
收割的总量一定，每天收割的公顷数与天数成反比例
原每天收割的公顷数×天数=现每天收割的公顷数×天数
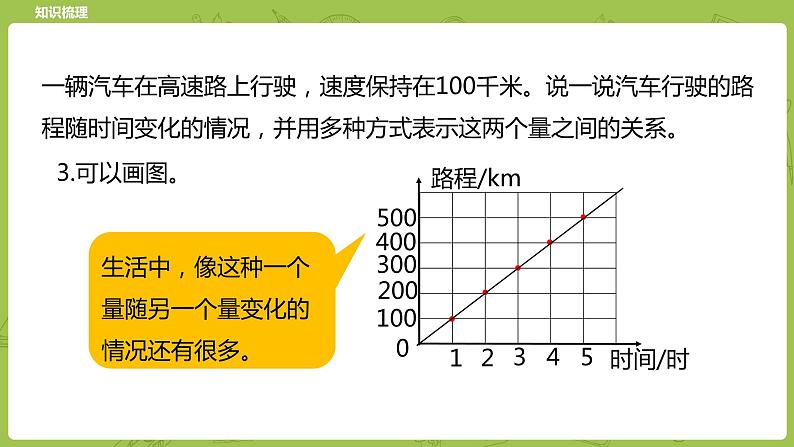
一辆汽车在高速路上行驶，速度保持在100千米。说一说汽车行驶的路程随时间变化的情况，并用多种方式表示这两个量之间的关系。
2.可以用式子来表示。
如果用t表示汽车行驶的时间，S表示汽车行驶的路程，那么
生活中，像这种一个量随另一个量变化的情况还有很多。
4.判断两种量成什么比例关系？
某工厂四月份（30天）计划生产一批零件，平均每天要生产400个才能完成任务，实际上前6天就生产了3000个。照这样计算，完成原计划任务要用多少天？（分别用正、反比例解）
答：完成原计划任务要用24天。
为什么同样的题目既可以用正比例解，也可以用反比例解呢？
我们仔细分析一下这两种解法，首先第二种解法是抓住“计划生产一批零件”我们知道了生产零件总个数是一定的，再根据“每天生产的零件个数×生产的天数＝原计划一共要生产的零件个数（积一定）”，因此，可以用反比例方法解答。
那么上面这道题这样的解法都对吗？为什么呢？
但是这道题如果从“实际上前6天就生产3000个。照这样计算。”这两个条件再分析得知：“生产的零件个数÷生产的天数＝每天生产的零件个数（商一定）”，因而可以用正比例的方法来解答。
修一条公路，总长12千米，开工3天修了1.5千米。照这样计算，修完这条路要多少天？
解：设修完这条公路还要x天。
答：修完这条路要24天。
工作效率一定,工作总量和时间成正比例
一个比例的两个内项都是质数,它们的积是10,一个外项是0.4,这个比例是多少?并求出另一个外项。
积是10的两个数并且又是质数的是2和5。
比一比，想一想，列比例求解。
每分钟加工零件的数量一定，加工总量和加工时间成正比例。
答：8分钟加工120 个。
加工总量一定，每分钟加工零件的数量和加工时间成反比例。
大齿轮与小齿轮的齿数比为4∶3。大齿轮有36个齿，小齿轮有多少个齿？
答：小齿轮有27个齿。
学校买来126米塑料绳,每9米能做5根跳绳。照这样计算,能做多少根跳绳?
磁悬浮列车匀速行驶时，路程与时间的关系如下。
1.图中的点A表示时间1分钟，磁悬浮列车驶过的路程为7km，请你试着描出其他各点。2.连接各点，它们在一条直线上吗？3.列车运行2.5分时，行驶的路程是多少？
（2）连接各点，它们在一条直线上。（3）列车运行2.5分时，行驶的路程是17.5km。