2020-2021学年鲁教版（五四制）七年级下册 期中复习试卷1（word版 含答案）

这是一份2020-2021学年鲁教版（五四制）七年级下册 期中复习试卷1（word版 含答案），共16页。试卷主要包含了下列四个命题，将一副三角板，下列说法正确的是等内容，欢迎下载使用。
2020-2021学年鲁教五四新版七年级下册数学期中复习试卷1
一．选择题（共12小题，满分48分，每小题4分）
1．方程组的解为，则被遮盖的前后两个数分别为（　　）
A．1、2 B．1、5 C．5、1 D．2、4
2．下列四个命题：①±4是64的立方根；②5是25的算术平方根；③如果两条直线都与第三条直线平行，那么这两条直线也互相平行；④在平面直角坐标系中，与两坐标轴距离都是2的点有且只有2个．其中真命题有（　　）个．
A．1 B．2 C．3 D．4
3．将一副三角板（∠A＝30°）按如图所示方式摆放，使得AB∥EF，则∠1等于（　　）

A．75° B．90° C．105° D．115°
4．下列说法正确的是（　　）
A．篮球队员在罚球线上投篮一次，则“投中”是随机事件
B．明天的降水概率为40%，则“明天下雨”是确定事件
C．任意抛掷一枚质地均匀的硬币10次，则“5次正面朝上”是必然事件
D．a是实数，则“|a|≥0”是不可能事件
5．如图，一飞镖游戏板由大小相等的小正方形格子构成，向游戏板随机投掷一枚飞镖，击中黑色区域的概率是（　　）

A． B． C． D．
6．某市举办中学生足球赛，按比赛规则，每场比赛都要分出胜负，胜1场得3分，负一场扣1分，菁英中学队在8场比赛中得到12分，若设该队胜的场数为x，负的场数为y，则可列方程组为（　　）
A． B．
C． D．
7．池塘中放养了鲤鱼2000条，鲢鱼若干条，在几次随机捕捞中，共捕到鲤鱼200条，鲢鱼300条，估计池塘中原来放养了鲢鱼（　　）
A．10000条 B．2000条 C．3000条 D．4000条
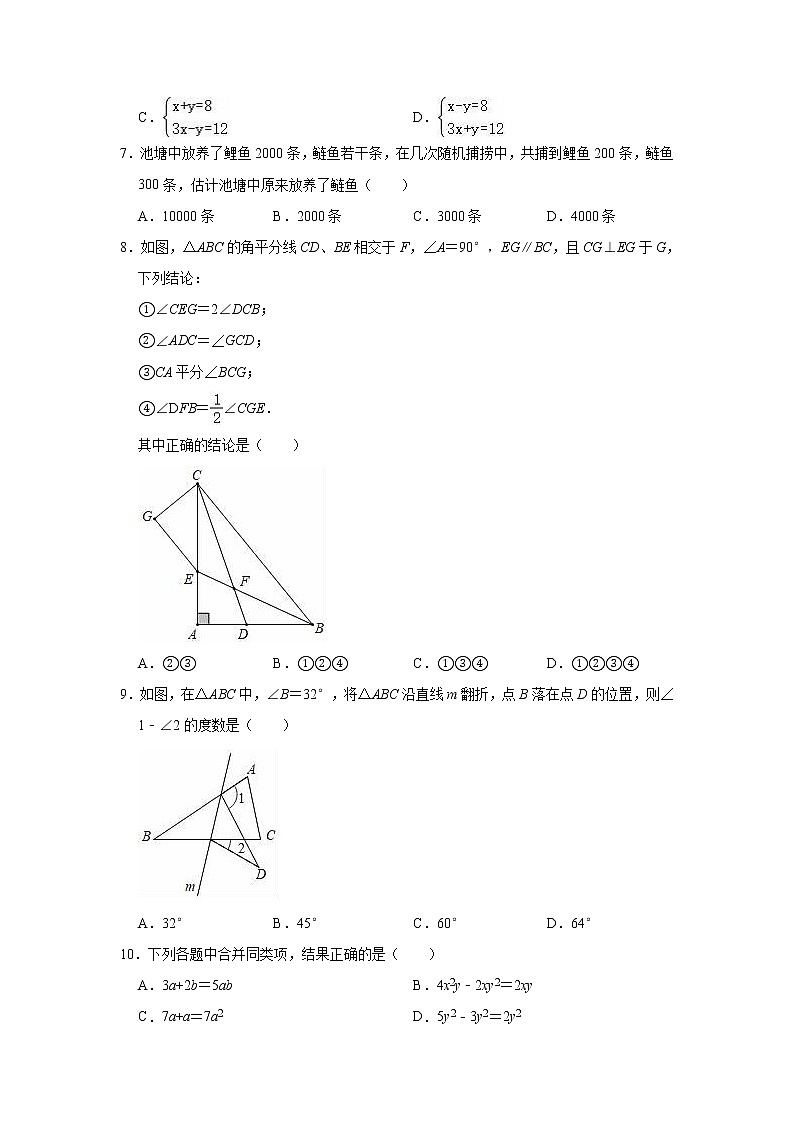
8．如图，△ABC的角平分线CD、BE相交于F，∠A＝90°，EG∥BC，且CG⊥EG于G，下列结论：
①∠CEG＝2∠DCB；
②∠ADC＝∠GCD；
③CA平分∠BCG；
④∠DFB＝∠CGE．
其中正确的结论是（　　）

A．②③ B．①②④ C．①③④ D．①②③④
9．如图，在△ABC中，∠B＝32°，将△ABC沿直线m翻折，点B落在点D的位置，则∠1﹣∠2的度数是（　　）

A．32° B．45° C．60° D．64°
10．下列各题中合并同类项，结果正确的是（　　）
A．3a+2b＝5ab B．4x2y﹣2xy2＝2xy
C．7a+a＝7a2 D．5y2﹣3y2＝2y2
11．已知直线y＝kx+2与直线y＝x交于点P，且点P的横坐标为2，下列结论：其中正确的是（　　）
①关于x的方程kx+2＝0的解为x＝3；
②对于直线y＝kx+2，当x＜3时，y＞0；
③方程组的解为，
A．①② B．①③ C．②③ D．①②③
12．把一副三角板放在水平桌面上，摆放成如图所示的形状，使两个直角顶点重合，两条斜边平行，则∠1的度数是（　　）

A．90° B．105° C．120° D．135°
二．填空题（共6小题，满分24分，每小题4分）
13．方程组的解是　 　．
14．有6张看上去无差别的卡片，上面分别写着0，π，，，0.1010010001，﹣随机抽取1张，则取出的数是无理数的概率是　 　．
15．如图，△ABC中，∠A＝55°，将△ABC沿DE翻折后，点A落在BC边上的点A′处．如果∠A′EC＝70°，那么∠A′DB的度数为　 　．

16．如图，直线a，b被c所截，∠1＝50°，若要a∥b，则需增加条件　 　（填图中某角的度数）；依据是　 　．

17．把命题“对顶角相等”改写成“如果…那么…”的形式：　 　．
18．将一列有理数﹣1，2，﹣3，4，﹣5，6…如图所示有序排列，4所在位置为峰1，﹣9所在位置为峰2…．
（1）处在峰5位置的有理数是　 　；
（2）2022应排在A，B，C，D，E中　 　的位置上．

三．解答题（共7小题，满分78分）
19．（6分）如图，已知，AB⊥BC，AD∥BC，∠BAC＝∠D＝60°．
（1）试求∠C和∠DEC的度数；
（2）说明直线AC与DE的关系，并说明理由．

20．（15分）解方程组
（1）；
（2）；
21．（9分）小明和小刚用如图所示的两个转盘做游戏，游戏规则如下：分别旋转两个转盘，当两个转盘所转到的数字之积为奇数时，小明得2分；当所转到的数字之积为偶数时，小刚得1分．这个游戏对双方公平吗？若公平，说明理由．若不公平，如何修改规则才能使游戏对双方公平？

22．（12分）如图，EF∥AD，AD∥BC，CE平分∠BCF，∠DAC＝120°，∠ACF＝20°，求∠FEC的度数．

23．（12分）某校组织“大手拉小手，义卖献爱心”活动，计划购买黑白两种颜色的文化衫进行手绘设计后出售，并将所获利润全部捐给山区困难孩子．已知该学校从批发市场花4800元购买了黑白两种颜色的文化衫200件，每件文化衫的批发价及手绘后的零售价如表：

批发价（元）
零售价（元）
黑色文化衫
25
45
白色文化衫
20
35
（1）学校购进黑、白文化衫各几件？
（2）通过手绘设计后全部售出，求该校这次义卖活动所获利润．
24．（12分）如图：已知在平面直角坐标系中点A（a，b）点B（a，0），且满足|2a﹣b|+（b﹣4）2＝0．
（1）求点A、点B的坐标．
（2）已知点C（0，b），点P从B点出发沿x轴负方向以1个单位每秒的速度移动．同时点Q从C点出发，沿y轴负方向以2个单位每秒的速度移动，某一时刻，如图所示且S阴＝S四边形OCAB，求点P移动的时间？
（3）在（2）的条件下，AQ交x轴于M，作∠ACO，∠AMB的角平分线交于点N，判断是否为定值，若是定值求其值；若不是定值，说明理由．

25．（12分）快车和慢车分别从A市和B市两地同时出发，匀速行驶，先相向而行，慢车到达A市后停止行驶，快车到达B市后，立即按原路原速度返回A市（调头时间忽略不计），结果与慢车同时到达A市．快、慢两车距B市的路程y1、y2（单位：km）与出发时间x（单位：h）之间的函数图象如图所示．
（1）A市和B市之间的路程是　 　km；
（2）求a的值，并解释图中点M的横坐标、纵坐标的实际意义；
（3）快车与慢车迎面相遇以后，再经过多长时间两车相距20km？


参考答案与试题解析
一．选择题（共12小题，满分48分，每小题4分）
1．解：将x＝2代入第二个方程可得y＝1，
将x＝2，y＝1代入第一个方程可得2x+y＝5
∴被遮盖的前后两个数分别为：5，1
故选：C．
2．解：①∵4是64的立方根，
∴①是假命题；
②∵5是25的算术平方根，
∴②是真命题；
③∵如果两条直线都与第三条直线平行，那么这两条直线也互相平行，
∴③是真命题；
④∵在平面直角坐标系中，与两坐标轴距离都是2的点有且只有4个，
∴④是假命题；
真命题的个数有2个，
故选：B．
3．解：∵AB∥EF，
∴∠BDE＝∠E＝45°，
又∵∠A＝30°，
∴∠B＝60°，
∴∠1＝∠BDE+∠B＝45°+60°＝105°，
故选：C．
4．解：A．篮球队员在罚球线上投篮一次，则“投中”是随机事件，此选项正确；
B．明天的降水概率为40%，则“明天下雨”是随机事件，此选项错误；
C．任意抛掷一枚质地均匀的硬币10次，则“5次正面朝上”是随机事件，此选项错误；
D．a是实数，则“|a|≥0”是必然事件，此选项错误；
故选：A．
5．解：黑色区域的面积＝3×3﹣×3×1﹣×2×2﹣×3×1＝4，
所以击中黑色区域的概率＝＝．
故选：C．
6．解：依题意得：．
故选：C．
7．解：由题意可得，
2000÷×
＝2000×
＝3000（条），
即估计池塘中原来放养了鲢鱼3000条，
故选：C．
8．解：∵EG∥BC，
∴∠CEG＝∠BCA，
∵CD平分∠ACB，
∴∠BCA＝2∠DCB，
∴∠CEG＝2∠DCB，故①正确，
∵CG⊥EG，
∴∠G＝90°，
∴∠GCE+∠CEG＝90°，
∵∠A＝90°，
∴∠BCA+∠ABC＝90°，
∵∠CEG＝∠ACB，
∴∠ECG＝∠ABC，
∵∠ADC＝∠ABC+∠DCB，∠GCD＝∠ECG+∠ACD，∠ACD＝∠DCB，
∴∠ADC＝∠GCD，故②正确，
假设AC平分∠BCG，则∠ECG＝∠ECB＝∠CEG，
∴∠ECG＝∠CEG＝45°，显然不符合题意，故③错误，
∵∠DFB＝∠FCB+∠FBC＝（∠ACB+∠ABC）＝45°，∠CGE＝45°，
∴∠DFB＝∠CGE，故④正确，
故选：B．

9．解：如图所示：
由折叠的性质得：∠D＝∠B＝32°，
根据外角性质得：∠1＝∠3+∠B，∠3＝∠2+∠D，
∴∠1＝∠2+∠D+∠B＝∠2+2∠B＝∠2+64°，
∴∠1﹣∠2＝64°．
故选：D．

10．解：（A）原式＝3a+2b，故A错误；
（B）原式＝4x2y﹣2xy2，故B错误；
（C）原式＝8a，故C错误；
故选：D．
11．解：当x＝2时，y＝x＝，则P（2，），
把P（2，）代入y＝kx+2得2k+2＝，解得k＝﹣，
∴直线y＝kx+2的解析式为y＝﹣x+2，
当y＝0时，﹣ x+2＝0，解得x＝3，
∴关于x的方程kx+2＝0的解为x＝3，所以①正确；
当y＞0，﹣ x+2＞0，解得x＜3，所以②正确；
∵直线y＝kx+2与直线y＝x交点为P（2，），
∴方程组的解为，所以③正确．
故选：D．
12．解：作直线OE平行于直角三角板的斜边．
可得：∠A＝∠AOE＝60°，∠C＝∠EOC＝45°，
故∠1的度数是：60°+45°＝105°．
故选：B．

二．填空题（共6小题，满分24分，每小题4分）
13．解：将x＝1代入x+y＝5，
∴y＝4，
∴方程组的解为：，
故答案为：，
14．解：在0，π，，，0.1010010001，﹣中，无理数有π，，共2个，
∴取出的数是无理数的概率是＝；
故答案为：．
15．解：由翻折的性质可知：∠ADE＝∠EDA′，∠AED＝∠A′ED＝（180°﹣70°）＝55°，
∵∠A＝55°，
∴∠ADE＝∠EDA′＝180°﹣55°﹣55°＝70°，
∴∠A′DB＝180°﹣140°＝40°，
故答案为40°．
16．解：∵∠3＝50°，1＝50°，
∴∠1＝∠3，
∴a∥b（同位角相等，两直线平行）．
故答案为：∠3＝50°；同位角相等；两直线平行．
17．解：题设为：两个角是对顶角，结论为：这两个角相等，
故写成“如果…那么…”的形式是：如果两个角是对顶角，那么这两个角相等，
故答案为：如果两个角是对顶角，那么这两个角相等．
18．解：（1）观察发现：峰n中，A位置的绝对值可以表示为：5n﹣3；
B位置的绝对值可以表示为：5n﹣2；
C位置（峰顶）的绝对值可以表示为：5n﹣1；
D位置的绝对值可以表示为：5n；
E位置的绝对值可以表示为：5n+1；
∴处在峰5位置的有理数是5×5﹣1＝24；
（2）根据规律，∵2022＝5×405﹣3，
∴2022应排在A的位置．
故答案为：（1）24；（2）A．
三．解答题（共7小题，满分78分）
19．解：如图所示：

（1）∵AB⊥BC，
∴∠B＝90°，
又∵∠BAC＝60°，∠BAC+∠C＝90°，
∴∠C＝30°，
又∵AD∥BC，
∴∠D＝∠DEC，
（2）AC⊥DE，理由如下，
∵∠D＝60°，
∴∠DEC＝60°，
又∵∠DEC+∠C+∠EFC＝180°，
∴∠EFC＝90°，
∴AC⊥DE．
20．解：（1），
①×2+②得：﹣9y＝﹣9，
解得：y＝1，
把y＝1代入②得：x＝1，
则方程组的解为；
（2）方程组整理得：，
①×2+②得：11x＝22，
解得：x＝2，
把x＝2代入①得：y＝3，
则方程组的解为．
21．解：公平．
画树状图得：
从表中可以得到：P积为奇数＝＝，P积为偶数＝＝，
∴小明的积分为×2＝，小刚的积分为×1＝＝．

22．解：∵EF∥AD，AD∥BC，
∴EF∥BC，
∴∠ACB+∠DAC＝180°，
∵∠DAC＝120°，
∴∠ACB＝60°，
又∵∠ACF＝20°，
∴∠FCB＝∠ACB﹣∠ACF＝40°，
∵CE平分∠BCF，
∴∠BCE＝20°，
∵EF∥BC，
∴∠FEC＝∠ECB，
∴∠FEC＝20°．
23．解：（1）设学校购进黑文化衫x件，白文化衫y件，
依题意，得：，
解得：．
答：学校购进黑文化衫160件，白文化衫40件．
（2）（45﹣25）×160+（35﹣20）×40＝3800（元）．
答：该校这次义卖活动共获得3800元利润．
24．解：（1）∵|2a﹣b|+（b﹣4）2＝0．
∴2a﹣b＝0，b﹣4＝0，
∴a＝2，b＝4，
∴点A的坐标为（2，4）、点B的坐标（2，0）；
（2）方法一：如图2，设P点运动时间为ts，则t＞2，所以P点坐标为（2﹣t，0），Q点坐标为（0，4﹣2t），
设直线AQ的解析式为y＝kx+4﹣2t，
把A（2，4）代入得2k+4﹣2t＝4，解得k＝t，
∴直线AQ的解析式为y＝tx+4﹣2t，
直线AQ与x轴交点坐标为（，0），
∴S阴影＝（+t﹣2）×4+××（2t﹣4），
而S阴＝S四边形OCAB，
∴（+t﹣2）×4+××（2t﹣4）＝×2×4，
整理得t2﹣3t＝0，
解得t1＝0（舍去），t2＝3，
∴点P移动的时间为3s；
方法二：过P点作PM⊥AC于M，QN⊥AB于N，如图，
易得四边形OPMC和四边形ACQN都为矩形，
S阴影＝S矩形OPMC+S矩形ACQN﹣S△AMC﹣S△AQN＝4（t﹣2）+2×2t﹣×t×4﹣×2t×2，
∵S阴＝S四边形OCAB，
∴4（t﹣2）+2×2t﹣×t×4﹣×2t×2＝×2×4，解得t＝3；
（3）为定值．理由如下：
如图3，∵∠ACO，∠AMB的角平分线交于点N，
∴∠ACN＝45°，∠1＝∠2，
∵AC∥BP，
∴∠CAM＝∠AMB＝2∠1，
∵∠ACN+∠CAM＝∠N+∠1，
∴45°+2∠1＝∠N+∠1，
∴∠N＝45°+∠1，
∵∠AMB＝∠APB+∠PAQ，
∴∠APB+∠PAQ＝2∠1，
∵∠AQC+∠OMQ＝90°，
而∠OMQ＝2∠1，
∴∠AQC＝90°﹣2∠1，
∴＝＝．


25．解：（1）由图可知，
A市和B市之间的路程是360km，
故答案为：360；
（2）根据题意可知快车速度是慢车速度的2倍，
设慢车速度为x km/h，则快车速度为2x km/h，
2（x+2x）＝360，
解得，x＝60
2×60＝120，
则a＝120，
点M的横坐标、纵坐标的实际意义是两车出发2小时时，在距B市120 km处相遇；
（3）快车速度为120 km/h，到达B市的时间为360÷120＝3（h），
方法一：
当0≤x≤3时，y1＝﹣120x+360，
当3＜x≤6时，y1＝120x﹣360，
y2＝60x，
当0≤x≤3时，
y2﹣y1＝20，即60x﹣（﹣120x+360）＝20，
解得，x＝，﹣2＝，
当3＜x≤6时，
y2﹣y1＝20，即60x﹣（120x﹣360）＝20，
解得，x＝，﹣2＝，
所以，快车与慢车迎面相遇以后，再经过或h两车相距20 km．
方法二：
设快车与慢车迎面相遇以后，再经过t h两车相距20 km，
当0≤t≤3时，60t+120t＝20，
解得，t＝；
当3＜t≤6时，60（t+2）﹣20＝120（t+2）﹣360，
解得，t＝．
所以，快车与慢车迎面相遇以后，再经过或h两车相距20 km．