

江苏省高邮市临泽中学2020-2021学年下学期高一开学数学质量检测试卷
展开2020-2021学年度第二学期高一开学质量检测
数学试卷
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把答案填涂在答题卡相应位置上
1. 集合,,则( )
A. B. C. D.
2.若集合M={x|x2<1},N={x|0≤x<2},则M∩N=( )
A.{x|﹣1<x<2} B.{x|0≤x<1} C.{x|0<x<1} D.{x|﹣1<x<0}
3.已知函数,若,且,则的取值范围是( )
A. B. C. D.
4.已知函数,若相邻两个极值点的距离为,且当时,取得最小值,将的图象向左平移m个单位,得到一个偶函数图象,则满足题意的m的最小正值为( )
A. B. C. D.
5.命题:“,”的否定为( )
A. , B. ,
C. , D. ,
6.函数的周期为( )
A. 2π B. π C. D.
7.函数的单调递增区间是( )
A. B. C. D.
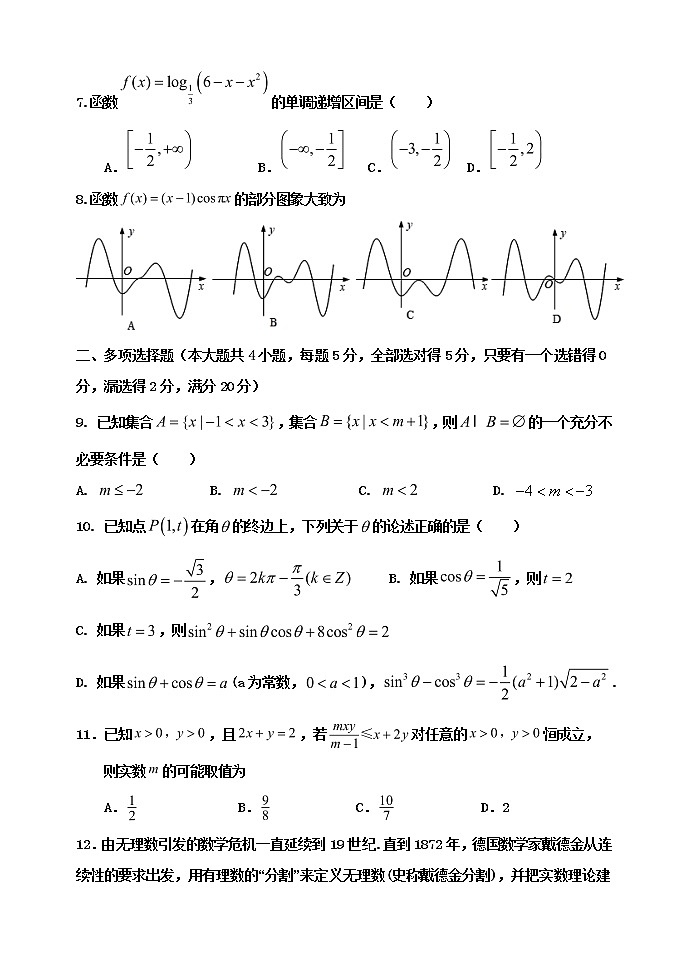
8.函数的部分图象大致为
二、多项选择题(本大题共4小题,每题5分,全部选对得5分,只要有一个选错得0分,漏选得2分,满分20分)
9. 已知集合,集合,则的一个充分不必要条件是( )
A. B. C. D.
10. 已知点在角的终边上,下列关于的论述正确的是( )
A. 如果, B. 如果,则
C. 如果,则
D. 如果(a为常数,),.
11.已知,且,若对任意的恒成立,
则实数的可能取值为
A. B. C. D.2
12.由无理数引发的数学危机一直延续到19世纪.直到1872年,德国数学家戴德金从连续性的要求出发,用有理数的“分割”来定义无理数(史称戴德金分割),并把实数理论建立在严格的科学基础上,才结束了无理数被认为“无理”的时代,也结束了持续2000多年的数学史上的第一次大危机.所谓戴德金分割,是指将有理数集划分为两个非空的子集与,且满足,,中的每一个元素都小于中的每一个元素,则称为戴德金分割.试判断下列选项中,可能成立的是( )
A.是一个戴德金分割
B.没有最大元素,有一个最小元素
C.有一个最大元素,有一个最小元素
D.没有最大元素,也没有最小元素
三、填空题:本大题共4小题,每小题5分,共20分.
13. 已知b克盐水中含有克盐,若给盐水加热,蒸发了克水后盐水更咸了,请将这一事实表示一个不等式:______.
14. 已知函数的图象的一条对称轴是直线,则的值为______.
15.将函数的图像上各点的横坐标缩短到原来的倍(纵坐标不变),再把得到的图像向左平移个单位长度得到函数的图像,则在区间上的值域为 .
16. 已知函数f(x)的定义域为R,对任意的实数x,有f(1-x)=f(1+x),当x≤1时,,则不等式的解集为____.
四、解答题:共6小题,共70分。请在答题卡指定区域内做答。解答时应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分)
已知,.
(1)若p为真,求实数x的取值范围;
(2)若p是q成立的充分不必要条件,求实数m的取值范围.
18. 已知.
(1)化简;
(2)若锐角满足,求值.
19. 在①②这两个条件中任选一个,补充在下面的问题中.
问题.已知全集U=R,A={x|2x-1<0},且_________,求
注:如果选择多个条件分别解答,按第一个解答计分.
20市博览会于2020年9月28日至11月28日在锦绣园举办,本届园林博览会以“辉煌荆楚,生态园博”为主题,展示当地生态之美,文化之韵,吸引更多优秀企业来荆投资,从而促进当地经济快速发展.在此次博览会期间,某公司带来了一种智能设备供采购商洽谈采购,并决定大量投放当地市场.
已知该种设备年固定研发成本为50万元,每生产一台需另投入80元,设该公司一年内生产该设备x万台且全部售完,每万台的销售收入(万元)与年产量x(万台)满足如下关系式:.
(Ⅰ)写出年利润(万元)关于年产量x(万台)的函数解析式;(利润=销售收入-成本)
(Ⅱ)当年产量为多少万台时,该公司获得的年利润最大?并求最大利润.
21. 已知函数.
(1)求函数的单调增区间;
(2)当时,函数有四个零点,求实数的取值范围.
22.已知a∈R,函数f(x)=log2(+a).
(1)设a>0,若对任意t∈[,1],函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过2,求a的最小值;
(2)若关于x的方程f()﹣log2[(a﹣2)x+3a﹣5]=0的解集中恰好只有一个元素,求a的取值范围.
参考答案
单选01-08 BBBAA CCB
多选9.BD 10. ACD 11.ACD 12.BD
填空13. 14. 15.
16. (或)
17.(1);(2).
(1)由得,解得,
所以p为真时,实数x的取值范围是;
(2)由,解得
若p是q成立的充分不必要条件,
则是的真子集,
所以 ,解得
所以实数m的取值范围是
18.(1);
(2)因为,且锐角,所以,所以,
则
.
19. 若选择①,;若选择②,
因为,所以,
若选择①,或,
所以.
若选择②,由得或,所以或,
所以.
20. 20.解:(Ⅰ).
(Ⅱ)当时,,
∴.
当时,
.
当且仅当即时等号成立,
∴.
∵,
∴当年产量为29万台时,该公司获得的利润最大为1360万元.
21(1),(2)
22.已知a∈R,函数f(x)=log2(+a).
(1)设a>0,若对任意t∈[,1],函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过2,求a的最小值;
(2)若关于x的方程f()﹣log2[(a﹣2)x+3a﹣5]=0的解集中恰好只有一个元素,求a的取值范围.
解:(1)因为在x∈[t,t+1]上为减函数,
所以,
又因为y=log2x在上为增函数,
所以,
所以在恒成立,
即对恒成立,
即3at2+3(a+1)t﹣1≥0对恒成立,
等价于y=3at2+3(a+1)t﹣1在的最小值大于等于0,
因为y=3at2+3(a+1)t﹣1在为增函数,
所以,
故,解得,
所以a的最小值为;
(2)方程f()﹣log2[(a﹣2)x+3a﹣5]=0,
即,
可转化为(a﹣2)x2+(2a﹣5)x﹣2=0且,
①当a﹣2=0,即a=2时,x=﹣2,符合题意;
②当a﹣2≠0,即a≠2时,,
1°当,即时,符合题意;
2°当,即a≠﹣2且时,
要满足题意,则有或,解得;
综上可得,a的取值范围为.
高邮市临泽中学2021-2022学年高二下学期期中模拟数学试卷: 这是一份高邮市临泽中学2021-2022学年高二下学期期中模拟数学试卷,共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2021-2022学年江苏省高邮市临泽中学高二下学期期中学情调研数学试题(Word版): 这是一份2021-2022学年江苏省高邮市临泽中学高二下学期期中学情调研数学试题(Word版),共13页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2021-2022学年江苏省高邮市临泽中学高二下学期期中学情调研数学试题含答案: 这是一份2021-2022学年江苏省高邮市临泽中学高二下学期期中学情调研数学试题含答案,共13页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












