浙教版七年级上册5.4 一元一次方程的应用图文ppt课件

这是一份浙教版七年级上册5.4 一元一次方程的应用图文ppt课件，共20页。PPT课件主要包含了古代曹冲称象，形状改变体积不变，方案如下，方案一，方案二，方案三，方案四，合作探究，解这个方程得x4，本题还有哪些解法等内容，欢迎下载使用。
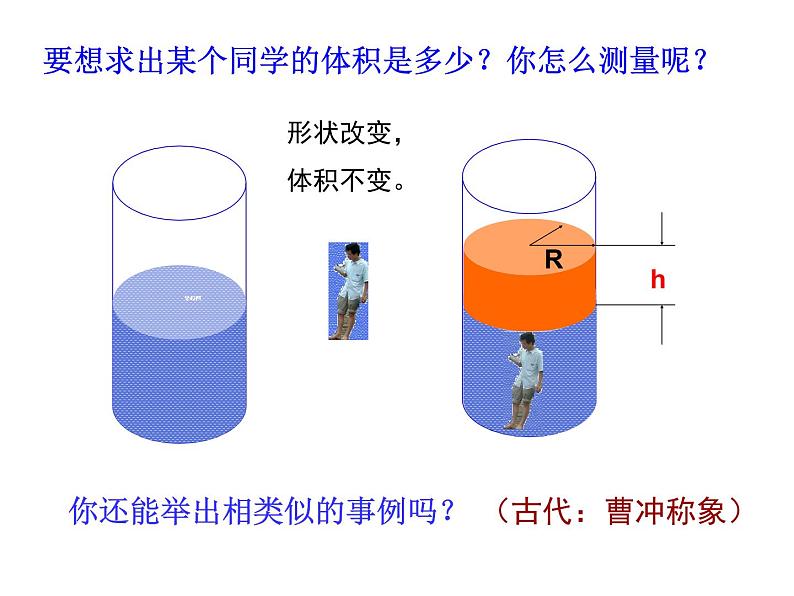
要想求出某个同学的体积是多少？你怎么测量呢？
你还能举出相类似的事例吗？
教学目标⒈继续体验方程是刻画现实世界的有效数学模型⒉掌握有关图形面积，体积计算和等积变形中常见的数量关系，进一步掌握分析数量关系， 并列出方程的方法
教学重点：掌握有关图形面积，体积计算和等积变形中常见的数量关系，进一步掌握分析数量关系， 并列出方程的方法教学难点：从问题情境 中找出用来列方程的不变量，需要较强的观察和分析能力，是本节的难点。
教材分析： 1、学生通过自学，小组合作能掌握的知识点是基本的面积公式，体积公式以及一些简单的数量关系 2、学生自学不能掌握的知识点在具体的问题中如何去寻找各种等量关系，如何设元及列方程，需要多找几个题目加以练习从中得到提升和巩固。
想一想： 请指出下列过程中，哪些量发生了变化，哪些量保持不变？1、把一小杯水倒入另一只大杯中； 2、用一根15cm长的铁丝围成一个三角形，然后把它围成长方形； 3、用一块橡皮泥先做成一个立方体，再把它改变成球。
解：水的底面积、高度发生了变化，水的体积和质量都保持不变
解：围成的图形的面积发生了变化，但铁丝的长度不变
解：形状改变，体积不变
自学书本128-129，思考下面问题：例题3中的阴影面积怎么表示，144块花岗岩的总面积是多少，两者有什么关系？例题4中长方体的体积和圆柱体的体积公式是什么，它们有什么关系？
一纪念碑建筑的底面呈正方形，其四周铺上花岗石，形成一个宽为3.2米的正方形边框（如图中阴影部分），已知铺这个边框恰好用了144块边长为0.8米的正方形花岗石（接缝忽略不计）,问纪念碑建筑底面的边长是多少米?
分析：如图,若用x表示中间空白正方形的边长，本题的等量关系是什么？
阴影部分的面积＝ 144块边长为0.8米的正方形花岗石的面积
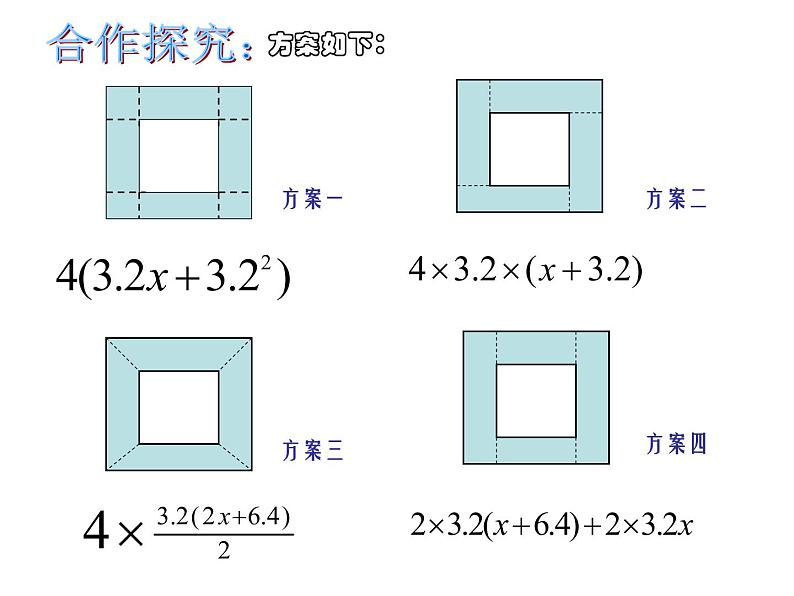
怎样用含x的代数式表示阴影部分的面积呢? 你能设计几种不同的计算方法。
一纪念碑建筑的底面呈正方形，其四周铺上花岗岩，形成一个宽为3.2米的正方形边框（如图中阴影部分），已知铺这个边框恰好用了144块边长为0.8米的正方形花岗岩,问纪念碑建筑底面的边长是多少米?
阴影部分的面积= 144块边长为0.8正方形花岗岩的面积阴影部分的面积= 4个长为(x+3.2)米、宽为3.2米的长方形
解： 设纪念碑建筑底面的边长为x米，根据题意，得
答：纪念碑建筑底面的边长为4米.
1、在应用方程解决问有关实际问题时，清楚地分辨量之间的关系，尤其相等关系是建立方程的关键。2、解题中的检验对确保答案的正确和合理很有帮助，但具体过程可省略不写。3、对于等积变形问题，它的基本数量关系是相关的面积公式，相等关系的特征是存在不变量，也就是用不同的方法来计算阴影部分的面积，面积不变。
例2：用直径为200mm的钢柱锻造一块长、宽、高分别为300mm，300mm，80mm的长方体毛坯底板，应截取圆柱多少长？（圆柱的体积=底面积×高。计算时，要求结果误差不超过1mm）
1.一书架能放厚为6.3cm 的书45本.现在准备 放厚为2.1cm 的书,问能放这种书多少本?
2、一种小麦磨成面粉后，质量将减少15%，为了得到5100千克面粉，需多少千克小麦？
如图，有A,B两个圆柱形容器，A容器的底面积是B容器底面积的2倍，B容器的壁高为22cm。已知A容器内装水的高度为10cm，若把这些水倒入B容器，水会溢出吗？
按图示的方法搭1个三角形需要3根火柴棒,搭2个三角形需要5根火柴棒.设共搭成n 个三角形,你怎样用关于是 n 的代数式表示n 个三角形需要火柴棒的根数? 现有2009根火柴棒,能搭几个这样的三角形? 2100根呢?
本节课同学们学到些什么？
1、善于利用图形的面积、体积、周长及质量等捕捉等量关系，从而列出方程。
如图一个铁片长30cm,宽20cm，打算从四个角各截去一个小正方形，然后把四边折起来做一个无盖的铁盒，铁盒的底面周长为60cm,问铁盒的高是多少？
铁盒的底面周长=60cm
例2、学校组织植树活动，已知在甲处植树的有23人，在乙处植树的有17人，现调20人去支援，使在甲处植树的人数是乙处植树人数的2倍，应调往甲、乙两处各多少人？
分析 : 设应调往甲处x人，题目中涉及的有关数量及其关系能用表格去表示吗？
甲处增加后人数=2×乙处增加后人数
解：设应调往甲处x人，根据题意，得 ２３＋x＝２（１７＋２０－x） 解这个方程，得x＝１７ ∴２０－x＝３ 答:应调往甲处１７人，乙处３人。
想一想：若设调往乙处的人数为x，方程又应怎样列?
２３+２０ － x＝２（１７＋x）
在解决实际问题时,我们一般可以通过分析实际问题, 抽象出数学问题, 然后运用数学思想方法解决问题.用列表分析数量关系是常用的方法.