初中数学华师大版八年级下册第19章 矩形、菱形与正方形19.1 矩形1. 矩形的性质习题课件ppt

这是一份初中数学华师大版八年级下册第19章 矩形、菱形与正方形19.1 矩形1. 矩形的性质习题课件ppt，共26页。

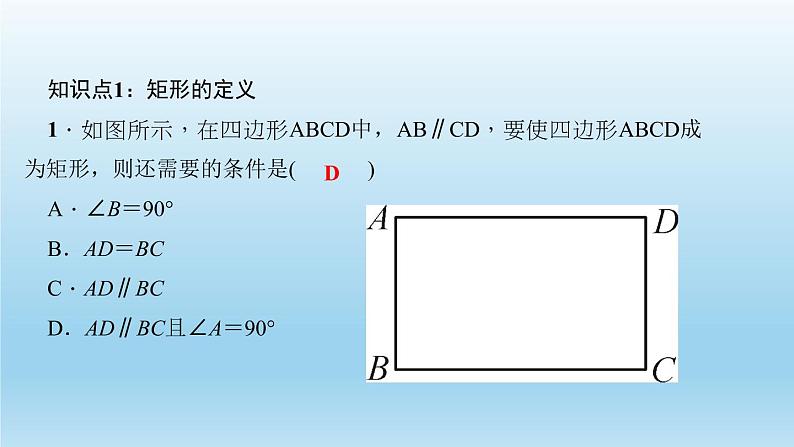
知识点1：矩形的定义1．如图所示，在四边形ABCD中，AB∥CD，要使四边形ABCD成为矩形，则还需要的条件是( )A．∠B＝90° B．AD＝BCC．AD∥BC D．AD∥BC且∠A＝90°
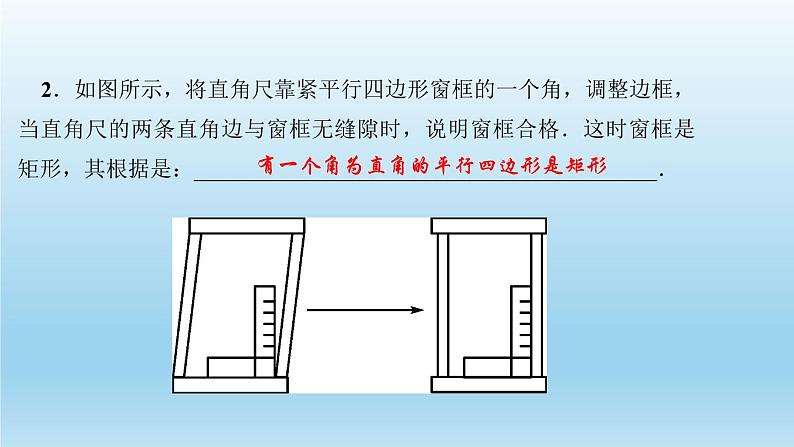
2．如图所示，将直角尺靠紧平行四边形窗框的一个角，调整边框，当直角尺的两条直角边与窗框无缝隙时，说明窗框合格．这时窗框是矩形，其根据是：__________________________________________．
有一个角为直角的平行四边形是矩形
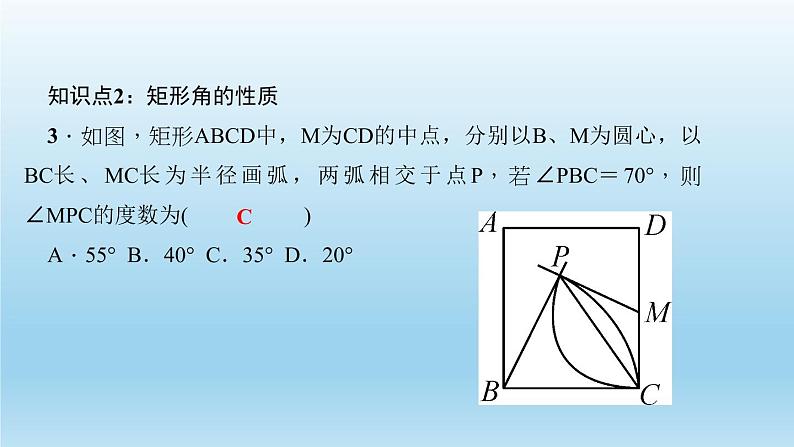
知识点2：矩形角的性质3．如图，矩形ABCD中，M为CD的中点，分别以B、M为圆心，以BC长、MC长为半径画弧，两弧相交于点P，若∠PBC＝70°，则∠MPC的度数为( )A．55° B．40° C．35° D．20°
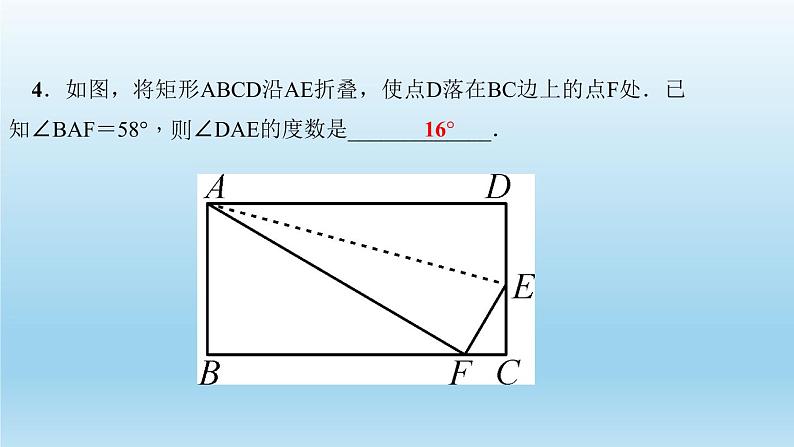
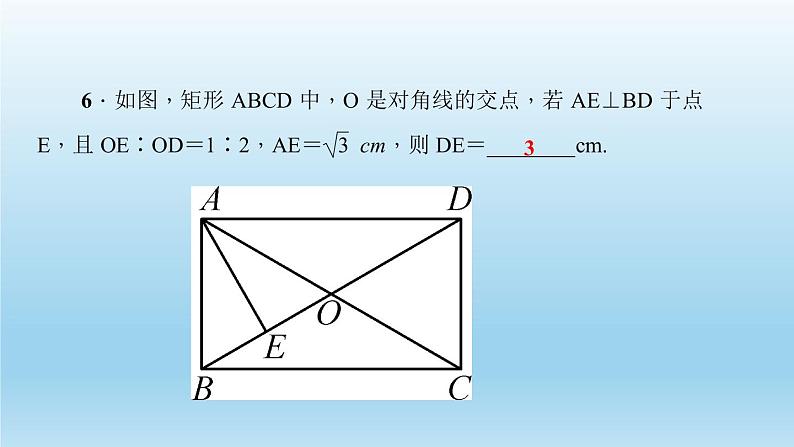
4．如图，将矩形ABCD沿AE折叠，使点D落在BC边上的点F处．已知∠BAF＝58°，则∠DAE的度数是_____________．
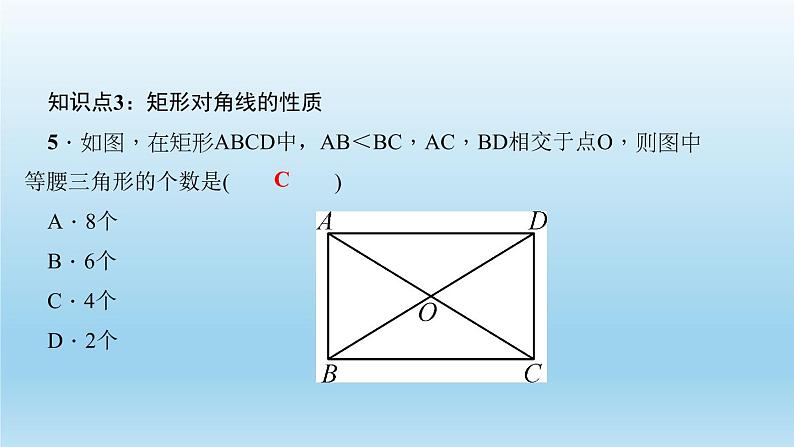
知识点3：矩形对角线的性质5．如图，在矩形ABCD中，AB＜BC，AC，BD相交于点O，则图中等腰三角形的个数是( )A．8个B．6个C．4个D．2个
7．如图所示，已知矩形ABCD被两条对角线分成四个小三角形，如果四个小三角形周长的和为86 cm，矩形的对角线长为13 cm，则矩形周长是_____________．
8．如图所示，已知四边形ABCD是矩形，对角线AC和BD相交于点O，CE∥DB交AB的延长线于点E，求证：AC＝CE.
证明：∵四边形ABCD是矩形，∴AC＝BD，AB∥CD，即BE∥CD.∵CE∥DB，∴四边形BECD是平行四边形，∴BD＝CE，∴AC＝CE.
易错点：不能利用矩形的性质对问题进行转化
9．如图，点A、D、G、M在半圆O上，四边形ABOC、DEOF、HMNO均为矩形．设BC＝a，EF＝b，NH＝c，则下列各式中正确的是( )A．a＞b＞c B．b＞c＞aC．c＞a＞b D．a＝b＝c
10．(2017·兰州)如图，矩形ABCD的对角线AC与BD交于点O，∠ADB＝30°，AB＝4，则OC＝( )A．5 B．4 C．3.5 D．3
11．如图，矩形ABCD的对角线AC和BD相交于点O，过点O的一直线分别交AD和BC于点E、F，AB＝2，BC＝3，则图中阴影部分的面积为( )A．3 B．4 C．5 D．6
14．(导学号19414097)如图所示，矩形ABCD中，AE平分∠BAD交BC于E，∠CAE＝15°，则下面的结论：①△ODC是等边三角形；②BC＝2AB；③∠AOE＝135°；④S△AOE＝S△COE，其中正确结论有( )A．1个 B．2个 C．3个 D．4个
15．(2016·巴中)如图，延长矩形ABCD的边BC至点E，使CE＝BD，连结AE，如果∠ADB＝30°，则∠E＝_____________．
17．如图，矩形ABCD的对角线交于点O，过点O作EF⊥AC分别交AD、BC于点E、F，求证：四边形AECF是平行四边形．
证明：∵四边形ABCD是矩形，∴AD∥BC，∴∠CAD＝∠ACB.∵EF⊥AC，∴∠AOE＝∠COF＝90°.∵点O为矩形ABCD对角线的交点，∴OA＝OC，∴△AOE≌△COF，∴AE＝CF.又∵AE∥CF，∴四边形AECF是平行四边形．
18．(导学号19414098)如图，在矩形ABCD中，E是AB边的中点，沿EC对折矩形ABCD，使点B落在点P处，折痕为EC，连结EC，连结AP并延长AP交CD于点F，连结BP，交CE于点H.(1)若∠PBA∶∠PBC＝1∶2，判断△PBC的形状并说明理由；(2)求证：四边形AECF为平行四边形．
解：(1)△PBC是等边三角形．理由：∵四边形ABCD是矩形，∴∠ABC＝90°.∵∠PBA∶∠PBC＝1∶2，∴∠PBC＝60°.∵沿EC对折矩形ABCD，使点B落在点P处，∴PC＝BC，∴△PBC是等边三角形．