2021年高考数学二轮复习课时跟踪检测08《由三视图求面积与体积》小题练(含答案详解)

这是一份2021年高考数学二轮复习课时跟踪检测08《由三视图求面积与体积》小题练(含答案详解)，共8页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。

一、选择题
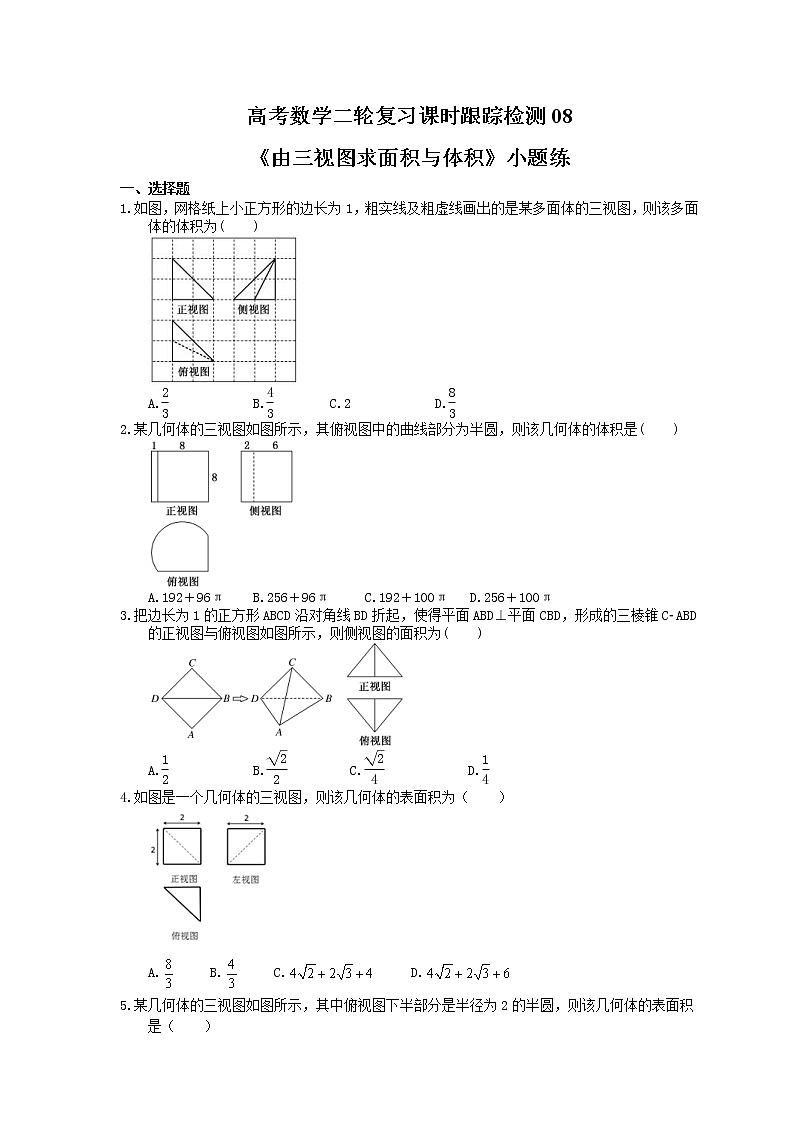
如图，网格纸上小正方形的边长为1，粗实线及粗虚线画出的是某多面体的三视图，则该多面体的体积为( )
A.eq \f(2,3) B.eq \f(4,3) C.2 D.eq \f(8,3)
某几何体的三视图如图所示，其俯视图中的曲线部分为半圆，则该几何体的体积是( )
A.192＋96π B.256＋96π C.192＋100π D.256＋100π
把边长为1的正方形ABCD沿对角线BD折起，使得平面ABD⊥平面CBD，形成的三棱锥C­ABD的正视图与俯视图如图所示，则侧视图的面积为( )
A.eq \f(1,2) B.eq \f(\r(2),2) C.eq \f(\r(2),4) D.eq \f(1,4)
如图是一个几何体的三视图，则该几何体的表面积为（ ）
A. B. C. D.
某几何体的三视图如图所示，其中俯视图下半部分是半径为2的半圆，则该几何体的表面积是（ ）
A. B. C. D.
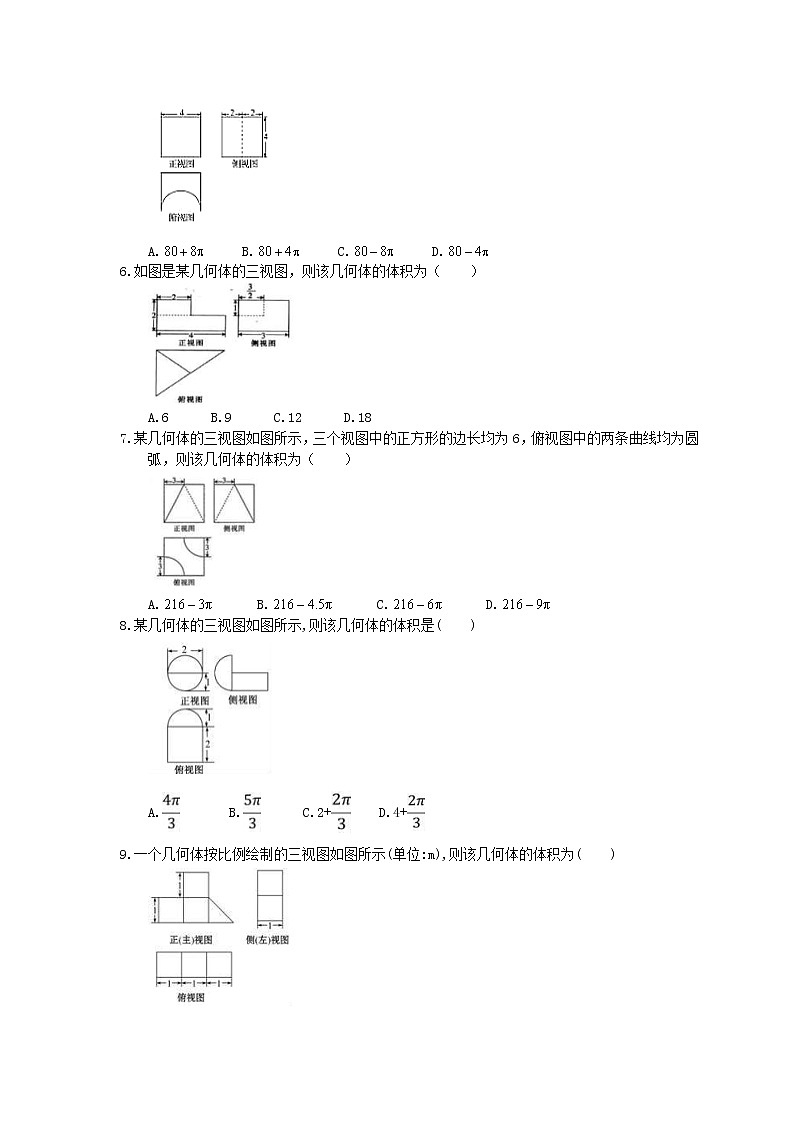
如图是某几何体的三视图，则该几何体的体积为（ ）
A.6 B.9 C.12 D.18
某几何体的三视图如图所示，三个视图中的正方形的边长均为6，俯视图中的两条曲线均为圆弧，则该几何体的体积为（ ）
A. B. C. D.
某几何体的三视图如图所示,则该几何体的体积是( )
A. B. C.2+ D.4+
一个几何体按比例绘制的三视图如图所示(单位:m),则该几何体的体积为( )
A. m3B.4.5 m3 C.3.5 m3 m3
如图是一个四棱锥的三视图,则该几何体的体积为（ ）
A. B. C. D.
某四面体的三视图如下图所示，该四面体的体积是（ ）
A.8 B. C.10 D.
已知一个三棱锥的三视图如图所示，其中三视图的长、宽、高分别为2，，，
且，则此三棱锥外接球表面积的最小值为（ ）
A. B. C. D.
二、填空题
某四面体的三视图如图所示，则该四面体高的最大值是__________.
三棱锥及其三视图中的主视图和左视图如图所示，则棱的长为__________.
某几何体的三视图如图所示，则该几何体最长边长是_____该几何体的体积是_______.
网格纸上小正方形的边长为1，粗虚、实线画出的是某个长方体挖去一个几何体得到的几何图形的三视图，则该被挖去的几何体的体积为__________.
\s 0 参考答案
答案为：A；
解析：由三视图可知，该几何体为三棱锥，将其放在棱长为2的正方体中，
如图中三棱锥A­BCD所示，故该几何体的体积V=eq \f(1,3)×eq \f(1,2)×1×2×2=eq \f(2,3).
答案为：C；
解析：题中的几何体是由一个直三棱柱和一个半圆柱构成的几何体，其中直三棱柱的底面是两直角边分别为8和6的直角三角形，高为8，该半圆柱的底面圆的半径为5，高为8，因此该几何体的体积为eq \f(1,2)×8×6×8＋eq \f(1,2)π×52×8=192＋100π，选C.
答案为：D；
解析：由三棱锥C­ABD的正视图、俯视图得三棱锥C­ABD的侧视图为直角边长是eq \f(\r(2),2)的等腰直角三角形，其形状如图所示，所以三棱锥C­ABD的侧视图的面积为eq \f(1,4)，故选D.
答案为：D
解析：由三视图还原该几何体如图：
其体积：，
故选D.
答案为：B
解析：根据三视图可知几何体是棱长为4的正方体挖掉半个圆柱所得的组合体，
且圆柱底面圆的半径是2、母线长是4，
∴该几何体的表面积，故选B.
答案为：B
解析：由已知中的三视图可得：该几何体是两个三棱柱形成的组合体，
下部的三棱柱，底面面积为，高为1，体积为6；
上部的三棱柱，底面面积为，高为1，体积为3；
故组合体的体积，故选B.
答案为：D
解析：几何体如下图所示，是一个正方体中挖去两个相同的几何体（它是个圆锥），
故体积为，故选D.
答案为：B；
解析：几何体是由直径为2的半球,和底面直径为2,高为2的半圆柱(被轴截面一分为二)构成,所以体积V=×πR3+×πR2h=×π·13+×π×12×2=.
答案为：C；
解析：该几何体是三个正方体和半个正方体的组合体,
所以几何体体积为3×13+×13=3.5(m3).
答案为：A
解析：根据几何体的三视图，得该几何体是如图所示的直四棱锥，
且四棱锥的底面为梯形，梯形的上底长为1，下底长为4，高为4；
所以，该四棱锥的体积为，故选A.
答案为：A
解析：由三视图可知该几何体是三棱锥，它的高是4，底面是直角三角形，
两直角边的长分别为3和4，故体积为，故选A.
答案为：B
解析：由已知条件及三视图得，此三棱锥的四个顶点位于长方体
的四个顶点，即为三棱锥，且长方体的长、宽、高分别为
2，，，
∴此三棱锥的外接球即为长方体的外接球，
且球半径为，
∴三棱锥外接球表面积为，
∴当且仅当，时，三棱锥外接球的表面积取得最小值为，故选B.
二、填空题
答案为：2
解析：如图是原几何体，
其在正方体中的位置，正方体棱长为2，则该四面体高的最大值为2，故答案为2.
答案为：
解析：由题意结合三视图可知，则.
答案为：，20
解析：由三视图还原可知，原图形为一个直三棱柱，切去了一个三棱锥剩下部分的图形，
如下图.
且，，，所以最长边为，
体积为.
答案为：2
解析：根据三视图知长方体挖去部分是一个底面为等腰梯形（上底为2，下底为4，高为2）高为2的直四棱柱，所以.