初中数学华师大版八年级下册第19章 矩形、菱形与正方形综合与测试课前预习课件ppt

这是一份初中数学华师大版八年级下册第19章 矩形、菱形与正方形综合与测试课前预习课件ppt，共24页。

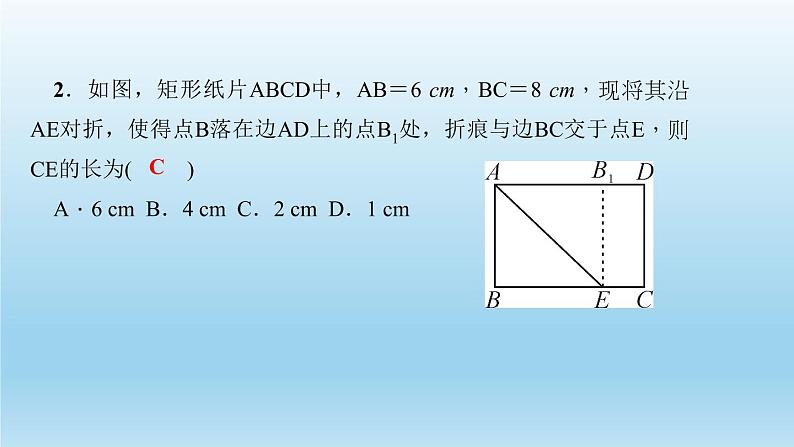
2．如图，矩形纸片ABCD中，AB＝6 cm，BC＝8 cm，现将其沿AE对折，使得点B落在边AD上的点B1处，折痕与边BC交于点E，则CE的长为( )A．6 cm B．4 cm C．2 cm D．1 cm
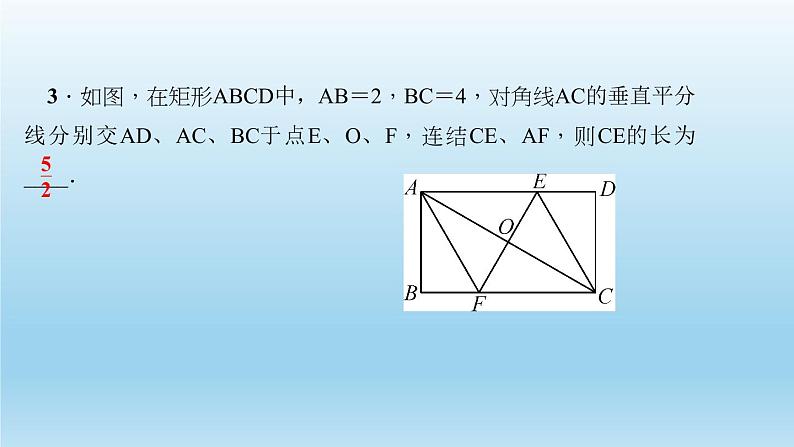
3．如图，在矩形ABCD中，AB＝2，BC＝4，对角线AC的垂直平分线分别交AD、AC、BC于点E、O、F，连结CE、AF，则CE的长为____．
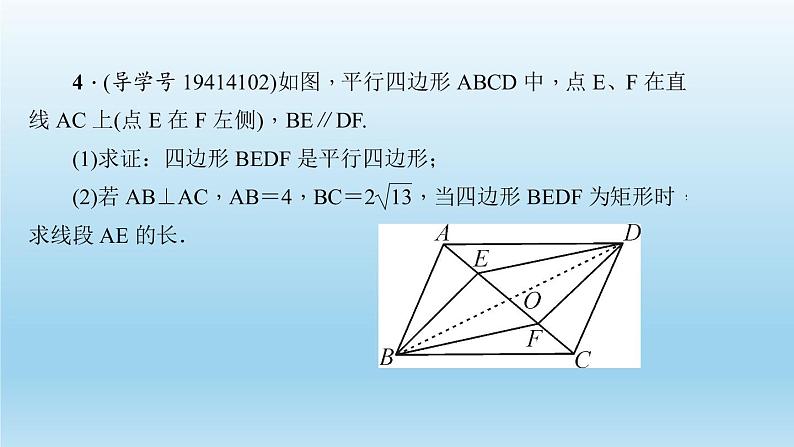
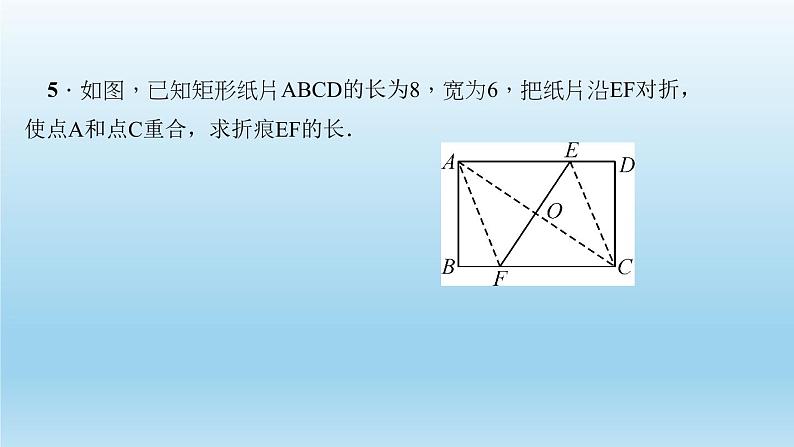
5．如图，已知矩形纸片ABCD的长为8，宽为6，把纸片沿EF对折，使点A和点C重合，求折痕EF的长．
类型二　综合利用矩形的判定解题6．在数学活动课上，老师和同学们判断一个四边形门框是否为矩形，下面是一个学习小组拟定的方案，其中正确的是( )A．测量对角线是否相互平分B．测量两组对边是否分别相等C．测量对角线是否相等D．测量其中三个角是否都为直角
7．如图，▱ABCD中，对角线AC、BD相交于点O，OA＝3，若要使平行四边形ABCD为矩形，则OB的长为( )A．4 B．3 C．2 D．1
8．如图，已知四边形ABCD，以下条件不能判别四边形ABCD是矩形的是( )A．AB＝CD，AD＝BC，∠A＝90°B．OA＝OB＝OC＝ODC．AB＝CD，AB∥CD，AC＝BDD．AB＝CD，AB∥CD，OA＝OC，OB＝OD
9．(导学号19414103)如图，在△ABC中，AB＝AC，D为BC边上一点，以AB、BD为邻边作平行四边形ABDE，连结AD、EC.(1)求证：△ADC≌△ECD；(2)当点D在什么位置时，四边形ADCE是矩形？请说明理由．
解：(1)证明：∵AB＝AC，∴∠B＝∠ACB.又∵▱ABDE中，AB＝DE，AB∥DE，∴∠B＝∠EDC＝∠ACB，AC＝DE.又∵DC＝CD，∴△ADC≌△ECD.
(2)当点D在BC的中点时，四边形ADCE是矩形．理由：∵四边形ABDE是平行四边形，∴AE＝BD，AE∥BC.∵D为BC的中点，∴BD＝CD，∴AE＝CD，AE∥CD，∴四边形ADCE是平行四边形．∵△ADC≌△ECD，∴AC＝DE，∴四边形ADCE是矩形．∴点D在BC的中点时，四边形ADCE是矩形．
10．如图，在▱ABCD中，∠ABD的平分线BE交AD于点E，∠CDB的平分线DF交BC于点F，连结BD.(1)求证：△ABE≌△CDF；(2)若AB＝DB，求证：四边形DFBE是矩形．
(2)∵△ABE≌△CDF，∴AE＝CF.∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC，∴DE∥BF，DE＝BF，∴四边形DFBE是平行四边形．∵AB＝DB，BE平分∠ABD，∴BE⊥AD，即∠DEB＝90°，∴平行四边形DFBE是矩形．
类型三　综合利用矩形的性质与判定解题11．已知▱ABCD的对角线AC、BD相交于点O，△AOB是等边三角形，AO＝4，则▱ABCD的面积为________．
12．(导学号19414104)如图，在▱ABCD中，点P是AB边上一点(不与A、B重合)，CP＝CD，过点P作PQ⊥CP，交AD边于点Q，连结CQ.(1)若∠BPC＝∠AQP，求证：四边形ABCD是矩形；(2)在(1)的条件下，当AP＝2，AD＝6时，求AQ的长．
解：(1)证明：∵∠BPQ＝∠BPC＋∠CPQ＝∠A＋∠AQP，∠BPC＝∠AQP，∴∠CPQ＝∠A.∵PQ⊥CP，∴∠A＝∠CPQ＝90°.又∵四边形ABCD是平行四边形，∴四边形ABCD是矩形．
13．(导学号19414105)如图，四边形ABCD中，对角线AC、BD相交于点O，AO＝CO，BO＝DO，且∠ABC＋∠ADC＝180°.(1)求证：四边形ABCD是矩形；(2)若DF⊥AC，∠ADF∶∠FDC＝3∶2，则∠BDF的度数是多少？
解：(1)证明：∵AO＝CO，BO＝DO，∴四边形ABCD是平行四边形，∴∠ABC＝∠ADC.∵∠ABC＋∠ADC＝180°，∴∠ABC＝∠ADC＝90°，∴四边形ABCD是矩形．