




华师大版七年级上册1 对顶角多媒体教学课件ppt
展开对顶角的定义对顶角的性质
2021/4/26 17:04
定义:两个角具有相同的顶点,并且一个角的两边与另一个角的两边互为反向延长线,我们把这样的两个角叫做对顶角.如图,∠1和∠3是对顶角,∠2和∠4也是对顶角.
例1 如图,直线a,b,c相交于一点,下面互为对角的一组角是( ) A.∠1与∠2 B.∠1与∠4 C.∠1与∠3 D.∠2与∠3
导引:判断两个角是不是对顶角,要紧扣对顶角的定义:∠1与∠2仅一边互为反向延长线,因此是对顶角;∠1与∠4的两边都不互为反向延长线,因此不是对顶角;∠1与∠3符合对顶角的定义;∠2与∠3的两边都不互为反向延长线,因此也不是对顶角.
判断两个角是否互为对顶角的方法:一看它们有没有公共顶点;二看这两个角的两边是否互为反向延长线,实质就是看这两个角是否是两条直线相交所成的没有公共边的两个角.
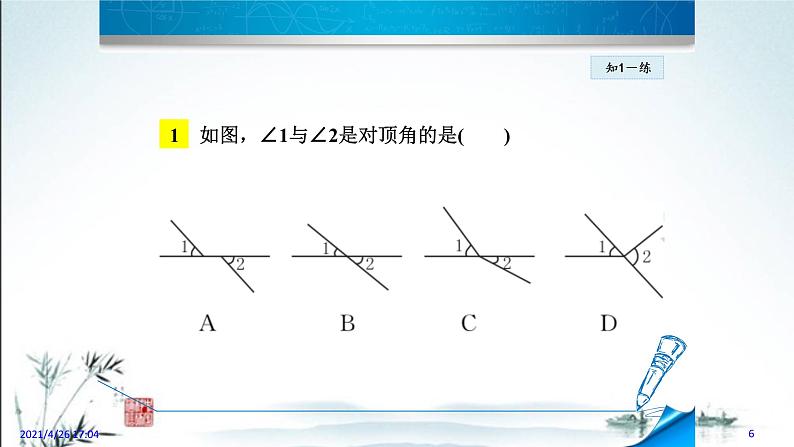
1 如图,∠1与∠2是对顶角的是( )
2 下列语句正确的是( ) A. 顶点相对的两个角是对顶角 B. 有公共顶点并且相等的两个角是对顶角 C. 两条直线相交,有公共顶点的两个角是对顶角 D. 两条直线相交,有公共顶点且没有公共边的两个 角是对顶角
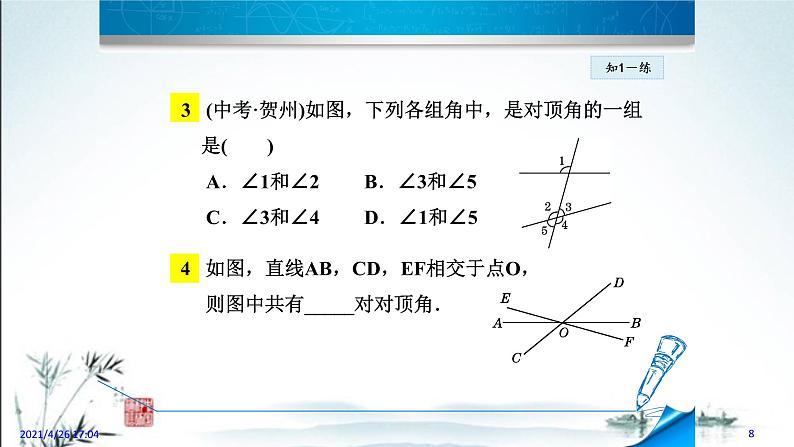
4 如图,直线AB,CD,EF相交于点O, 则图中共有_____对对顶角.
3 (中考·贺州)如图,下列各组角中,是对顶角的一组 是( ) A.∠1和∠2 B.∠3和∠5 C.∠3和∠4 D.∠1和∠5
例2 在图中,∠1=30。,那么∠2、∠3和∠4 各等 于多少度?图中存在哪些相等关系? 解:∠2 = 180°-∠1 =180°-30° = 150°, ∠3 = 180°- ∠2 = 180°-150° =30°, ∠4 = 180°-∠1 =180°-30° = 150°. 由此,我们得到 ∠1 = ∠3,∠2 =∠4.
对顶角的性质:对顶角相等.
例3 如图,直线AB、CD相交于点E,∠AEC=50。,求 ∠BED的度数.
解:因为直线AB、CD相交于点 E,所以∠AEC与∠BED是 对顶角.根据对顶角相等,得 ∠BED =∠AEC = 50°.
例4 如图,已知直线AB,CD,EF相交于点O, ∠DOE =90°,∠AOE=36°,求∠BOC的度数.
导引:因为∠BOC=∠AOD,∠BOC =∠BOF+∠COF,所以有两 种途径;求∠AOD或∠BOF, ∠COF;而它们都可由已知∠DOE =90°,∠AOE=36°求出.
解法一:因为直线AB、CD相交于点O, 所以∠BOC=∠AOD(对顶角相等). 因为∠DOE=90°,∠AOE=36°, 所以∠AOD=∠DOE+∠AOE=90°+36°=126°. 所以∠BOC=∠AOD=126°. 解法二:因为直线AB,CD,EF相交于点O, 所以∠COF=∠DOE,∠BOF=∠AOE(对顶角相等). 因为∠DOE=90°, ∠AOE=36°, 所以∠COF=90°, ∠BOF=36°. 所以∠BOC=∠COF+∠BOF =126°.
在进行计算或证明时,“对顶角相等”这个结论常常被用来将要求的角和特征相同的两个角转化成与已知条件相关的角;即对顶角构建了一个已知条件和待求结论之间的“桥梁”.
例5 如图,OC平分∠AOB,反向延长OC至D,反向 延长OA至E,∠3=25°,求∠BOE的度数.
导引:由图可知∠BOE+∠AOB= 180°,故要求∠BOE的度 数,只需求出∠AOB的度数 即可.因为OC平分∠AOB,即∠AOB=2∠2, 所以只需求出∠2的度数即可求出∠AOB的度数.
解:由对顶角相等,得∠2=∠3=25°. 因为OC平分∠AOB, 所以∠AOB=2∠2=50°. 又因为∠BOE与∠AOB互为邻补角, 所以∠BOE=180°-∠AOB=180°-50°=130°.
本例把两直线相交所成的角与角平分线有机地结合在一起,通过邻补角及对顶角反映不同位置上的角之间的关系,求角及证明相关角之间的关系是解决几何问题的一种重要手段.
1 如图,直线 AB,CD相交于点O,若∠1=30°,则 ∠2,∠3的度数分别为( ) A.120°,60° B.130°,50° C.140°,40° D.150°,30°
2 如图,三条直线AB,CD,EF相交于一点O,则 ∠AOE+∠DOB+∠COF等于( ) A.150° B.180° C.210° D.120°
3 如图,直线AB,CD相交于点O,∠AOC=75°, OE把∠BOD分成两部分,且∠BOE∶∠EOD= 1∶2,则∠AOE=( ) A.165° B.155° C.150° D.130°
华师大版七年级上册1 对顶角评课ppt课件: 这是一份华师大版七年级上册1 对顶角评课ppt课件,共15页。PPT课件主要包含了对顶角的定义,对顶角条件,邻补角互补,说一说,议一议等内容,欢迎下载使用。
初中数学华师大版七年级上册1 对顶角教学演示课件ppt: 这是一份初中数学华师大版七年级上册1 对顶角教学演示课件ppt,共15页。PPT课件主要包含了学习目标,新课引入,对顶角的概念,新课讲解,对顶角,随堂即练,对顶角的性质,对顶角相等,课堂小结等内容,欢迎下载使用。
初中数学华师大版七年级上册1 对顶角教学ppt课件: 这是一份初中数学华师大版七年级上册1 对顶角教学ppt课件,共14页。













