2021年云南省曲靖市罗平县中考数学模拟试卷

这是一份2021年云南省曲靖市罗平县中考数学模拟试卷，共6页。试卷主要包含了下列计算正确的是，下列事件中，是随机事件的是，如果﹣a＝2，则a＝　 　，分解因式等内容，欢迎下载使用。
一．选择题（满分32分，每小题4分）
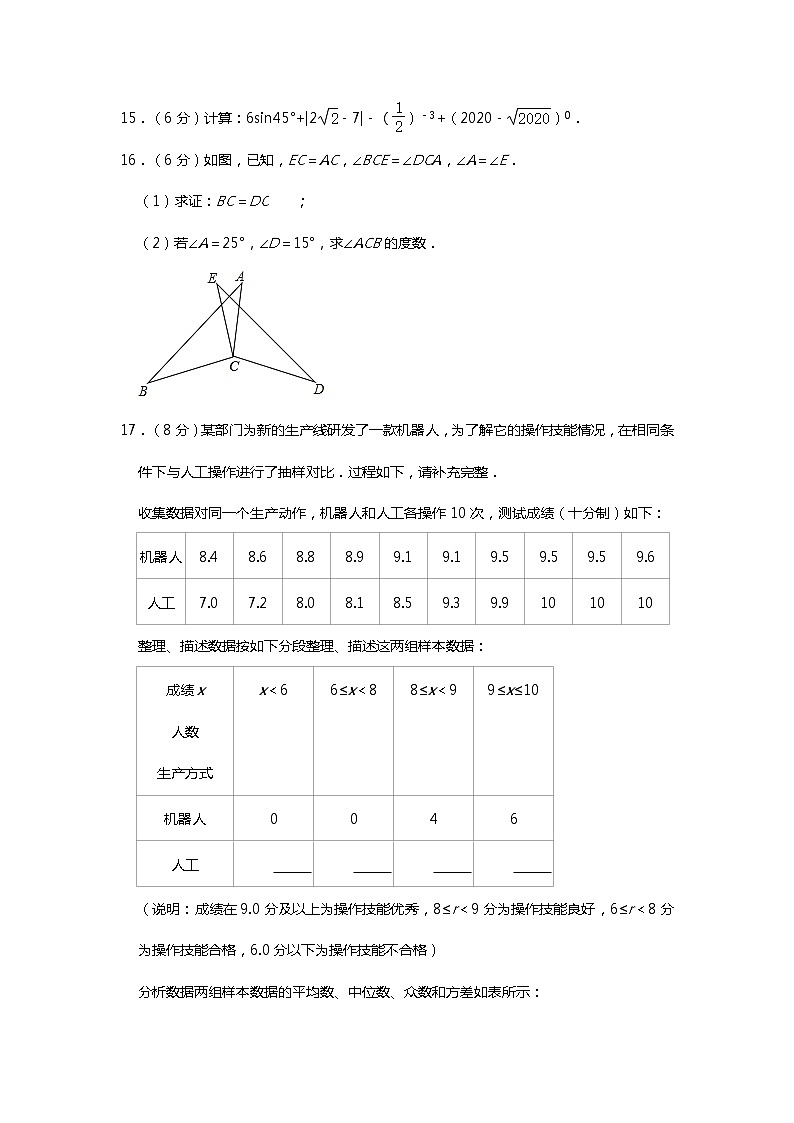
1．如图所示的几何体的从左面看到的图形为（ ）
A．B．C．D．
2．下列把2034000记成科学记数法正确的是（ ）
A．2.034×106B．20.34×105C．0.2034×106D．2.034×103
3．下列计算正确的是（ ）
A．2a4+3a4＝5a8B．（3a2）3＝9a6
C．5a2•4a2＝20a2D．a2•a3＝a5
4．若正多边形的一个外角是60°，则这个正多边形的边数是（ ）
A．4B．5C．6D．7
5．下列事件中，是随机事件的是（ ）
A．画一个三角形，其内角和是180°
B．投掷一枚正六面体骰子，朝上一面的点数为5
C．在只装了红色卡片的袋子里，摸出一张白色卡片
D．明天太阳从东方升起
6．一项工程，甲单独做a天完成，乙单独做b天完成．甲乙两人合做这项工程需要的时间是（ ）天．
A．B．C．D．
7．已知圆锥的底面半径为6cm，母线长为10cm，则这个圆锥的全面积是（ ）
A．60πcm2B．96πcm2C．132πcm2D．168πcm2
8．已知关于x的分式方程＝+2的解满足﹣4＜x＜﹣1，且k为整数，则符合条件的所有k值的乘积为（ ）
A．正数B．负数C．零D．无法确定
二．填空题（满分18分，每小题3分）
9．如果﹣a＝2，则a＝ ．
10．分解因式：2n2﹣8＝ ．
11．两个角的两边两两互相平行，且一个角的等于另一个角的，则这两个角中较小角的度数为 °．
12．函数中，自变量x的取值范围是 ．
13．已知反比例函数y＝的图象经过点（2，﹣4），则k的值为 ．
14．如图，在平面直角坐标系中，矩形ABCO的边CO、OA分别在x轴、y轴上，点E在边BC上，将该矩形沿AE折叠，点B恰好落在边OC上的F处．若OA＝6，AB＝10，则点E的坐标是 ．
三．解答题
15．（6分）计算：6sin45°+|2﹣7|﹣（）﹣3+（2020﹣）0．
16．（6分）如图，已知，EC＝AC，∠BCE＝∠DCA，∠A＝∠E．
（1）求证：BC＝DC；
（2）若∠A＝25°，∠D＝15°，求∠ACB的度数．
17．（8分）某部门为新的生产线研发了一款机器人，为了解它的操作技能情况，在相同条件下与人工操作进行了抽样对比．过程如下，请补充完整．
收集数据对同一个生产动作，机器人和人工各操作10次，测试成绩（十分制）如下：
整理、描述数据按如下分段整理、描述这两组样本数据：
（说明：成绩在9.0分及以上为操作技能优秀，8≤r＜9分为操作技能良好，6≤r＜8分为操作技能合格，6.0分以下为操作技能不合格）
分析数据两组样本数据的平均数、中位数、众数和方差如表所示：
得出结论：
（1）请结合数据分析写出机器人在操作技能方面两条优点；
（2）如果生产出一个产品，需要完成同样的操作200次，估计机器人生产这个产品达到操作技能优秀的次数为 ．
18．（6分）列二元一次方程组解应用题：
小颖家离学校1880米，其中有一段为上坡路，另一段为下坡路．她跑步去学校共用了16分钟，已知小颖在上坡路上的平均速度是80米/分钟，在下坡路上的平均速度是200米/分钟．求小颖上坡、下坡各用了多长时间？
19．（7分）有四张正面分别写有数字：20，15，10，5的卡片，背面完全相同，将卡片洗匀后背面朝上放在桌面上，小明先随机抽取一张，记下牌面上的数字（不放回），再从剩下的卡片中随机抽取一张，记下牌面上的数字．如果卡片上的数字分别对应价值为20元，15元，10元，5元的四件奖品，请用列表或画树状图法求小明两次所获奖品总值不低于30元的概率？
20．（8分）如图，在▱ABCD中，对角线AC，BD交于点O，E是AD上一点，连接EO并延长，交BC于点F．连接AF，CE，EF平分∠AEC．
（1）求证：四边形AFCE是菱形；
（2）若∠DAC＝60°，AC＝2，求四边形AFCE的面积．
21．（8分）某商店销售一种商品，经市场调查发现：当该商品的售价是50元时，可以销售100件，且利润为1000元；当该商品的售价是60元时，可以销售80件，且利润为1600元．
（1）该商品的进价是多少元/件？
（2）当用字母x表示商品的售价，用字母y表示商品的销售量时，发现本题中x，y的值总是满足关系式：y＝kx+b，请同学们根据题目提供的数据求出k，b的值，并求出当售价为70元时，销售利润是多少？
（3）在第2问的基础上，商品的销售量y与商品的售价x的关系保持不变，当商品的售价为80元时，每售出一件商品将捐赠a（a＞0）元给希望工程，要使最大利润不小于1400，求出a的取值范围．
22．（9分）如图，已知二次函数y＝ax2+bx+c（a≠0）的图象与x轴交于点A（﹣1，0），与x轴交于另一点B，与y轴交于点C（0，3），对称轴是直线x＝1，顶点是点M．
（1）求二次函数的解析式；
（2）求△MBC的面积；
（3）过原点的直线l平分△MBC面积，求l的解析式．
23．（12分）对于平面内⊙C和⊙C外一点P，若过点P的直线l与⊙C有两个不同的公共点M，N，点Q为直线l上的另一点，且满足（如图1所示），则称点Q是点P关于⊙O的密切点．
已知在平面直角坐标系xOy中，⊙O的半径为2，点P（4，0）．
（1）在点D（﹣2，1），E（1，0），F（3，）中，是点P关于⊙O的密切点的为 ．
（2）设直线l方程为y＝kx+b，如图2所示，
①k＝﹣时，求出点P关于O的密切点Q的坐标；
②⊙T的圆心为T（t，0），半径为2，若⊙T上存在点P关于⊙O的密切点，直接写出t的取值范围．
机器人
8.4
8.6
8.8
8.9
9.1
9.1
9.5
9.5
9.5
9.6
人工
7.0
7.2
8.0
8.1
8.5
9.3
9.9
10
10
10
成绩x
人数
生产方式
x＜6
6≤x＜8
8≤x＜9
9≤x≤10
机器人
0
0
4
6
人工




平均数
中位数
众数
方差
机器人
9.1

9.5

人工

8.9

1.28