




中考冲刺-数学-第13课 反比例函数及其图像
展开要点梳理1.概念: 函数 叫做反比例函数.2.图象: 反比例函数的图象是双曲线,不与两坐标轴相交的两条双曲线.3.性质: (1)当k>0时,其图象位于第一、三象限 ,在每个象限内,y随x的增大而减小; (2)当k<0时,其图象位于第二、四象限,在每个象限内,y随x的增大而增大; (3)其图象是关于原点对称的中心对称图形,又是轴对称图形.4.应用: 如图,点A和点C是反比例函数 的图象上任意两点,画AB⊥x轴于B,CD⊥y轴于D,则有S△AOB=S△COD=
第13课 反比例函数及其图象
考点巩固测试 1. 已知图中的曲线是反比例函数 图象的一支.(1)这个反比例函数图象的另一支在第几象限?常数m的取值范围是什么?解 这个反比例函数图象的另一支在第三象限. ∵m-5>0,∴m>5.(2)若该函数的图象与正比例函数y=2x的图象在第一象限内的交点为A,过A点作x轴的垂线,垂足为B,当△OAB的面积为4时,求点A的坐标及反比例函数的解析式. 解 ∵点A在直线y=2x上, ∴设点A的坐标为(x0,2x0)(x0>0), 则点B的坐标为(x0,0). ∵S△OAB=4, ∴ ½ ·x0·2x0=4,x02=4,x0=±2(舍去负值), ∴点A的坐标为(2,4).
感悟提高 一次函数与比例函数的图象的性质取决于系数的值,同样由图象的性质,反过来也可以确定系数的符号.要熟记函数的性质并灵活应用这些性质.变式测试1 (2013·聊城) 如图,已知一次函数y=kx+b的图象交反比例函数 图象于点A、B,交x轴于点C. (1)求m的取值范围; (2)若点A的坐标是(2,-4),且= 求m的值和一次函数的解析式.
解 (1)∵反比例函数的图象在第四象限,∴4-2m<0,解得m>2. (2)∵点A(2,-4)在反比例函数图象上,解 ∵点A(2,-4)在反比例函数图象上,过点A、B分别作AM⊥OC于点M,BN⊥OC于点N,∴∠BNC=∠AMC=90°.又∵∠BCN=∠ACM,∴△BCN∽△ACM, ∵AM=4,∴BN=1,∴点B的纵坐标为-1.∵点B在反比例函数的图象上,∴当y=-1时,x=8,∴点B的坐标为(8,-1).∵一次函数y=kx+b的图象过点A(2,-4),B(8,-1),
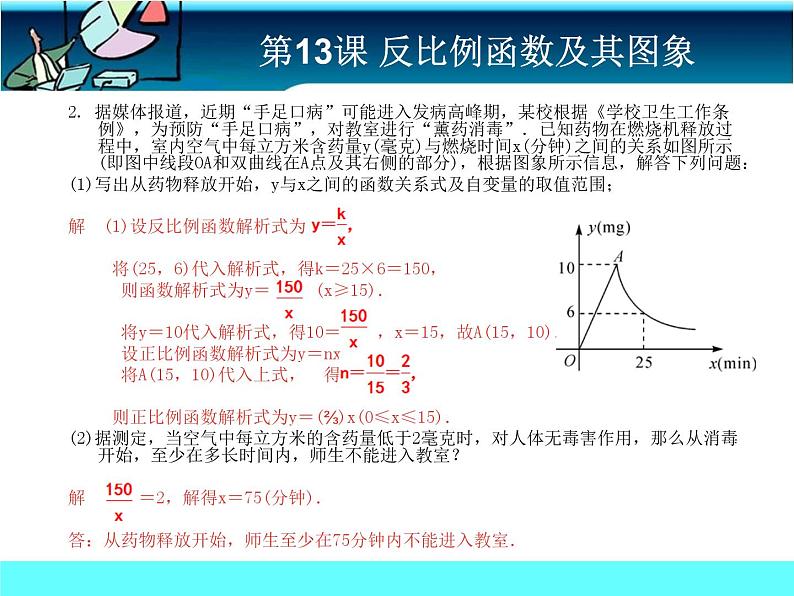
2. 据媒体报道,近期“手足口病”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“手足口病”,对教室进行“薰药消毒”.已知药物在燃烧机释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示(即图中线段OA和双曲线在A点及其右侧的部分),根据图象所示信息,解答下列问题:(1)写出从药物释放开始,y与x之间的函数关系式及自变量的取值范围; 解 (1)设反比例函数解析式为 将(25,6)代入解析式,得k=25×6=150, 则函数解析式为y= (x≥15). 将y=10代入解析式,得10= ,x=15,故A(15,10). 设正比例函数解析式为y=nx, 将A(15,10)代入上式, 得 则正比例函数解析式为y=(⅔)x(0≤x≤15).(2)据测定,当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始,至少在多长时间内,师生不能进入教室?解 =2,解得x=75(分钟).答:从药物释放开始,师生至少在75分钟内不能进入教室.
感悟提高 现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.若问题中两个变量不是单一的一次函数或反比例函数关系,而是二者的复合,则应分段讨论,并注意在实际问题中提炼出函数模型,往往要加自变量的取值范围.变式测试2 (2013·烟台) 如图,在平面直角坐标系中,A、B两点的纵坐标分别为7和1,直线AB与y轴所夹锐角为60°. (1)求线段AB的长; (2)求经过A、B两点的反比例函数的解析式.解 (1)分别过点A、B作AC⊥x轴,BD⊥AC,垂足分别为点C、D,由题意,知∠BAC=60°,AD=7-1=6,
(2)将等腰梯形ABCD向上平移2个单位后,问点B是否落在双曲线上? 解 将等腰梯形ABCD向上平移2个单位后得到梯形A′B′C′D′,得点B′(6,2),故当x=6时,y=12/6=2,即点B′恰好落在双曲线上. 3.如图,等腰梯形ABCD放置在平面坐标系中,已知A(-2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C. (1)求点C的坐标和反比例函数的解析式; 解 过点C作CE⊥AB于点E,∵四边形ABCD是等腰梯形,∴AD=BC,DO=CE,∴△AOD≌△BEC,∴AO=BE=2,∵BO=6,∴DC=OE=4,∴C(4,3).
感悟提高 C点的纵坐标与D点的纵坐标相同,过点C作CE⊥AB于点E,则△AOD≌△BEC,即可求得BE的长度,则OE的长度即可求得,即可求得C点的横坐标,然后利用待定系数法即可求得反比例函数的解析式;将等腰梯形ABCD向上平移2个单位后,点B向上平移2个单位长度得到的点的坐标即可得到,代入函数解析式判断即可. 本题是反比例函数与梯形的综合题,以及待定系数法求函数的解析式,利用数形结合解决此类问题,是非常有效的方法.
4.(2013·宜宾) 如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3),B(-4,0). (1)求经过点C的反比例函数的解析式; (2)设P是(1)中所求函数图象上一点,以P、O、A为顶点的三角形的面积与△COD的面积相等.求点P的坐标. 解 (1)由题意知,OA=3,OB=4, 在Rt△AOB中, ∵四边形ABCD为菱形, ∴AD=BC=AB=5,∴C(-4,-5). 设经过点C的反比例函数的解析式为y= 则 =-5,解得k=20, ∴所求的反比例函数的解析式为y= (2)设P(x,y), ∵AD=AB=5,OA=3, ∴OD=2,S△COD=(½)×2×4=4,即(½)·OA·|x|=4,
《中考大一轮数学复习》课件 课时15 反比例函数及其图像: 这是一份《中考大一轮数学复习》课件 课时15 反比例函数及其图像,共18页。PPT课件主要包含了夯实基本知已知彼,知识结构梳理,课前预测你很棒,热点看台快速提升等内容,欢迎下载使用。
《中考大一轮数学复习》课件 课时15 反比例函数及其图像: 这是一份《中考大一轮数学复习》课件 课时15 反比例函数及其图像,共18页。PPT课件主要包含了夯实基本知已知彼,知识结构梳理,课前预测你很棒,热点看台快速提升等内容,欢迎下载使用。
中考冲刺-数学-第14课 二次函数及其图像: 这是一份中考冲刺-数学-第14课 二次函数及其图像,共16页。PPT课件主要包含了考点跟踪训练等内容,欢迎下载使用。












