中考冲刺-数学-第20课 线段、角、相交线和平行线

这是一份中考冲刺-数学-第20课 线段、角、相交线和平行线，共14页。PPT课件主要包含了考点跟踪训练等内容，欢迎下载使用。

要点梳理1．线段沿着一个方向无限延长就成为射线；线段向两方无限延长就成为直线；线段是直线上两点间的部分，射线是直线上某一点一旁的部分．2．直线的基本性质：两点确定一条直线 ．线段的基本性质：两点之间线段最短 ，连结两点的线段的长度 ，叫做两点之间的距离．3．有公共端点的两条射线所组成的图形叫做角，也可以把角看成是由一条射线绕着它的端点旋转而成的图形．　　(1)1周角＝2平角＝4直角＝360° ，1°＝60′ ，1′＝60″ ．　　(2)小于直角的角叫做锐角；大于直角而小于平角的角叫做钝角；度数是90°的角叫做直角．4．两个角的和等于90°时，称这两个角互为余角 ，同角(或等角)的余角相等．两个角的和等于180°时，称这两个角互为补角 ，同角(或等角)的补角相等．5．角平分线和线段中垂线的性质：角平分线上的点到角两边的距离相等．线段中垂线上的点到线段两个端点的距离相等 ．到角两边的距离相等的点在角平分线上．到线段两个端点的距离相等的点在线段的中垂线上．6．两条直线相交，只有一个交点 ．两条直线相交形成四个角，我们把其中相对的每一对角叫做对顶角，对顶角相等．7．两条直线相交所组成的四个角中有一个是直角时，我们说这两条直线互相垂直，其中的一条直线叫做另一条直线的垂线，它们的交点叫做垂足．从直线外一点到这条直线的垂线段的长度 ，叫做点到直线的距离．连接直线外一点与直线上各点的所有线段中垂线段最短 ．
第20课　线段、角、相交线和平行线
8．垂直于一条线段并且平分这条线段的直线，叫做这条线段的垂直平分线 ，也叫线段的中垂线．9．在同一平面内不相交的两条直线叫做平行线．经过直线外一点，有且只有一条直线和这条直线平行．10．平行线的判定及性质：　　(1)判定：　　　　①在同一平面内不相交的两条直线叫做平行线；　　　　②同位角相等，两直线平行；　　　　③内错角相等，两直线平行；　　　　④同旁内角互补 ，两直线平行；　　　　⑤在同一平面内垂直于同一直线的两直线平行；　　　　⑥平行于同一直线的两直线平行．　　(2)性质：　　①两直线平行，同位角相等；　　②两直线平行，内错角相等；　　③两直线平行，同旁内角互补．两个重要公理　　(1)直线公理：经过两点有且只有一条直线．简称：两点确定一条直线．“有”表示存在性；“只有”体现“唯一性”，直线公理也称直线性质公理．　　(2)线段公理：两点之间，线段最短．
考点巩固测试 1.　已知E、F两点把线段AB分成2∶3∶4三部分，D是线段AB的中点，FB＝12，求DF的长及AE∶AD.　　　解　　　　　　　　　如图，设AE＝2x，EF＝3x，FB＝4x，则AB＝9x.　　　∵D是AB的中点，∴AD＝BD＝4.5x.　　　∵FB＝12，∴4x＝12，x＝3.　　　又∵AF＝2x＋3x＝5x，　　　∴DF＝5x－4.5x＝0.5x＝0.5×3＝1.5.　　　∴AE∶AD＝2x∶4.5x＝2∶4.5＝4∶9.感悟提高　　在解答有关线段的计算问题时，一般要注意以下几个方面：　　①按照题中已知条件画出符合题意的图形是正确解题的前提条件；　　②学会观察图形，找出线段之间的关系，列算式或方程来解答．
变式测试1　在直线l上，线段AB＝7 cm，BC＝3 cm，D是AC的中点，求DB的长度．　　　解　(1)当点C在线段AB延长线上，如图： 有AC＝AB＋BC＝7＋3＝10.　　　∵D是AC的中点，　　　∴DB＝AB－AD＝7－5＝2(cm)．　　　(2)当点C在线段AB上，如图：　　　有AC＝AB－BC＝7－3＝4.　　　∵D是AC的中点，∴AD＝CD＝½AC＝2.　　　∴DB＝DC＋CB＝2＋3＝5(cm)．　　　综上，DB的长度为2 cm或5 cm.
2.如图，直线AB、CD相交于点O，OE⊥AB，垂足为O，如果∠EOD＝42°，则∠AOC＝________．解析　∵OE⊥AB，∴∠AOE＝90°.∴∠AOC＋∠EOD＝180°－∠AOE＝90°.∵∠EOD＝42°，∴∠AOC＝90°－42°＝48°.感悟提高 当已知中有“相交线”出现的时候，要充分挖掘其中隐含的“邻补角和对顶角”，以帮助解题．变式测试2　(1)(2013·宁波) 如图，直线AB与直线CD相交于点O，E是∠AOD内一点，已知OE⊥AB，∠BOD＝45°，则∠COE的度数是(　　)　　A．125° B．135° C．145° D．155°　　　解析　∵OE⊥AB，∴∠EOA＝90°.　　　∵∠AOC＝∠BOD＝45°，　　　∴∠COE＝∠EOA＋∠AOC＝90°＋45°＝135°.
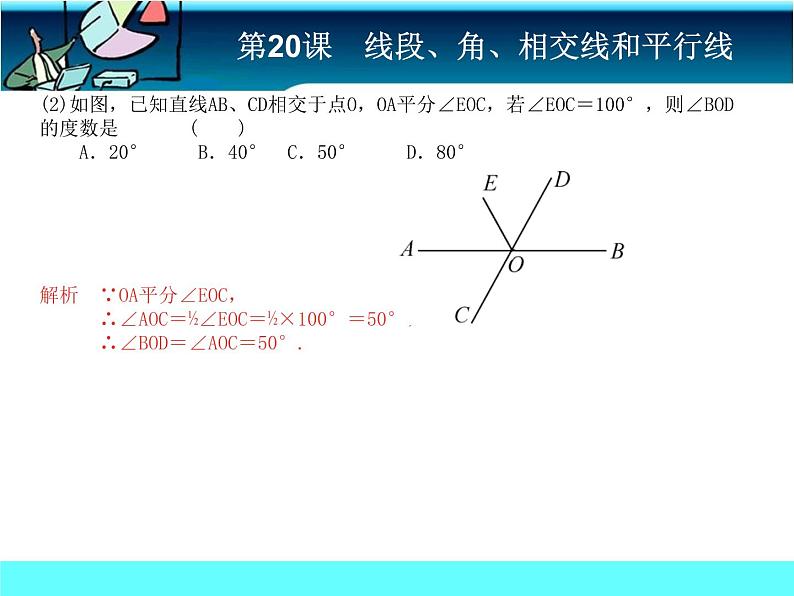
(2)如图，已知直线AB、CD相交于点O，OA平分∠EOC，若∠EOC＝100°，则∠BOD的度数是 (　　)　　A．20° B．40° C．50° D．80° 　　　解析　∵OA平分∠EOC，　　　∴∠AOC＝½∠EOC＝½×100°＝50°，　　　∴∠BOD＝∠AOC＝50°.
3.(1)(2013·张家界) 如图，直线a、b被直线c所截，下列说法正确的是 (　　)　　A．当∠1＝∠2时，一定有a∥b B．当a∥b时，一定有∠1＝∠2　　C．当a∥b时，一定有∠1＋∠2＝90° D．当∠1＋∠2＝180°时，一定有a∥b解析　A．若∠1＝∠2，不符合a∥b的条件，故本选项错误；B．若a∥b，则∠1＋∠2＝180°，∠1不一定等于∠2，故本选项错误；C．若a∥b，则∠1＋∠2＝180°，故本选项错误；D．如图，由于∠1＝∠3，当∠3＋∠2＝180°时，a∥b，所以当∠1＋∠2＝180°时，一定有a∥b，故本选项正确．(2)如图，a∥b，M、N分别在a、b上，P为两平行线间一点，求∠1＋∠2＋∠3之和．
解　思路一：延长MP交b于Q，　　　∵a∥b，∴∠1＝∠4，　　　∴∠1＋∠2＋∠3＝∠4＋∠2＋∠3，　　　∵△PQN的三外角之和等于360°，　　　∴∠1＋∠2＋∠3＝360°.思路二：连接MN，则原∠1被分成∠5、∠6之和，原∠3被分成∠7、∠8之和，∵∠5＋∠8＝180°，∠2＋∠6＋∠7＝180°，∴∠1＋∠2＋∠3＝(∠6＋∠2＋∠7)＋(∠5＋∠8)＝360°.　　　 思路三：过P画c∥a，　　　∵a∥b，∴c∥b，　　　则原∠2被分成∠9、∠10之和，　　　∵∠1＋∠9＝180°，∠3＋∠10＝180°，　　　∴∠1＋∠2＋∠3＝360°.
感悟提高　　本例中集中给出了多种辅助线的作法，以构造平行线或构造“三线八角”基本图形为主要原则，利用平行线的性质求角度．变式测试3　(2012·连云港) 如图，将三角尺的直角顶点放在直线a上，a∥b，∠1＝50°，∠2＝60°，则∠3＝(　　) 　　A．50° 　　　B．60° C．70° 　　　D．80°　　　解析　∵∠1＝50°，∠2＝60°，　　　∴∠4＝180°－∠1－∠2　　　＝180°－50°－60°＝70°，　　　∴∠5＝∠4＝70°，　　　∵a∥b，　　　∴∠3＝∠5＝70°.
4.　阅读下列材料并填空：(1)探究：平面上有n个点(n≥2)且任意3个点不在同一条直线上，经过每两点画一条直线，一共能画多少条直线？ 我们知道，两点确定一条直线，平面上有2个点时， 可以画(2X1）/2＝1(条)直线；平面内有3个点时，一共可以画(3x2)/2＝3(条)直线；平面上有4个点时，一共可以画(4x3)/2＝6(条)直线；平面内有5个点时，一共可以画________条直线……平面上有n个点时，一共可以画_____ ___条直线．(2)迁移：某足球比赛中有n个球队(n≥2)进行单循环比赛(每两队之间必须比赛一场)，一共要进行多少场比赛？ 有2个球队时，要进行(2x1)/2＝1(场)比赛，有3个球队时，要进行(3x2)/2＝3(场)比赛，有4个球队时，要进行______场比赛．感悟提高　　此题给出了几种特殊情况，从分子、分母数字的变化规律也可以得到探究结果，熟记本题的探究结果，对解决一些问题会有所帮助．
变式测试4　(1)(2013·柳州)如图，点A、B、C是直线l上的三个点，图中共有线段条数是 (　　) 　　 A．1条 B．2条 C．3条 D．4条　　　解析　有三条线段AB、AC、BC.(2)在某次商业聚会中，聚会结束后同桌的六个客人都互相握了手，聚会开始时这六个客人也都互相问了好，那么，他们一共有多少次握手，多少次问好？