初中数学人教版八年级下册18.2.1 矩形教学演示ppt课件

这是一份初中数学人教版八年级下册18.2.1 矩形教学演示ppt课件，共24页。PPT课件主要包含了学习目标，举例讲解，探索新知，对边平行且相等，对角相等邻角互补，对角线互相平分，矩形的一般性质，矩形特殊的性质，数学语言，矩形的对角线相等等内容，欢迎下载使用。
1.掌握矩形的概念和性质，理解矩形与平行四边形的　区别与联系.重点
2.会初步运用矩形的概念和性质来解决有关问题.难点
下面这些物体是什么形状,它们是轴对称图形吗?有几条对称轴?
　　当独木桥前后运动时，四边形ABCD是什么形状？当独木桥最后停下时，四边形ABCD有什么特殊的变化？当独木桥静止时，四边形ABCD是什么图形？
　　有一个角是直角 的平行四边形叫做矩 形．
　　小学中学习过的长方形是矩形吗？正 方形是矩形吗？
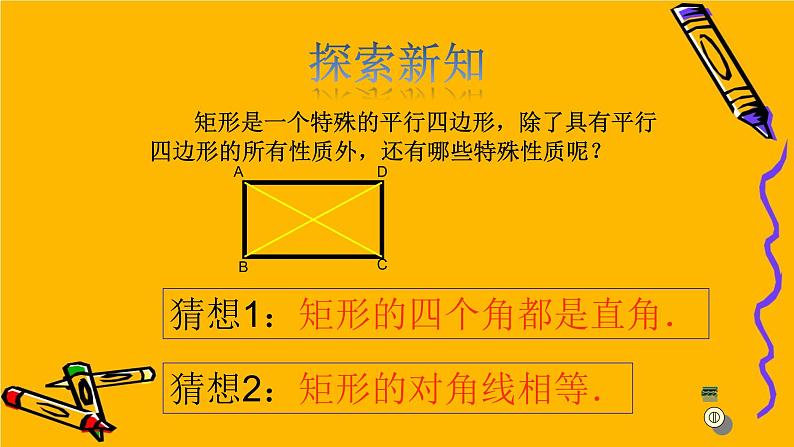
矩形是一个特殊的平行四边形，除了具有平行四边形的所有性质外，还有哪些特殊性质呢？
猜想1：矩形的四个角都是直角．
猜想2：矩形的对角线相等．
求证：矩形的四个角都是直角．
已知：如图，四边形ABCD是矩形,
求证：∠A=∠B=∠C=∠D=90°.
证明： ∵四边形ABCD是矩形,
又 矩形ABCD是平行四边形,
∴ ∠A=∠C ∠B = ∠D. ∠A +∠B = 90°.
∴ ∠A=∠B=∠C=∠D=90°,即矩形的四个角都是直角.
已知：如图,四边形ABCD是矩形, 求证：AC = BD.
证明：在矩形ABCD中,
∵∠ABC = ∠DCB = 90°,
又∵AB = DC ， BC = CB,
∴△ABC≌△DCB.
∴AC = BD, 即矩形的对角线相等.
求证:矩形的对角线相等
矩形的四个角都是直角．
矩形的两条对角线相等．
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=900
矩形的四个角都是直角；
矩形的对角线相等且互相平分；
公平,因为OA=OC=OB=OD
　　例1　如图，矩形ABCD的两条对角线相交于点O，且∠AOB=60°，AB=4 cm．求矩形对角线的长．
2. 过四边形的各个顶点分别作对角线的平行线，若这四条平行线围成一个矩形，则原四边形一定是
1. 下面性质中，矩形不一定具有的是
　A．对角线相等 B．四个角都相等 C．是轴对称图形 D．对角线垂直
A．对角线相等的四边形 B．对角线互相平分且相等的四边形C．对角线互垂直平分的四边形 D．对角线垂直的四边形
[ ]
4. 矩形ABCD中，AB=2BC，E在CD上，AE=AB，则∠BAE等于
　A．30° B．45° C．60° D．120°
3. 已知矩形的一条对角线与一边的夹角是40°，则两条对角线所夹锐角的度数为
5. 如图，矩形ABCD被两条对角线分成四个小三角形，如果四个小三角形的周长的和是86cm,对角线长是13cm，那么矩形的周长是多少？
解： ∵ △AOB、 △BOC、 △COD和△AOD四个三角形的周长和为86cm,又∵
AC=BD=13cm,
∴ 　　AB+BC+CD+DA =86－2(AC+BD)
=86－4×13=34(cm).
即矩形ABCD的周长等于34cm.
　　直角三角形斜边上的中线等于斜边的一半．　　矩形是轴对称图形，连接对边中点的直线是它的两条对称轴．
矩形的对边平行且相等；矩形的四个角都是直角；矩形的对角线相等且互相平分．
矩形：有一个角是直角的平行四边形叫做矩形．
３.已知如图，O是矩形ABCD对角线的交点，AE平分∠BAD，∠AOD=1200，求∠EAO的度数和∠OEA的度数 。